1.DFS (Depth First Search) 深度优先搜索

其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次

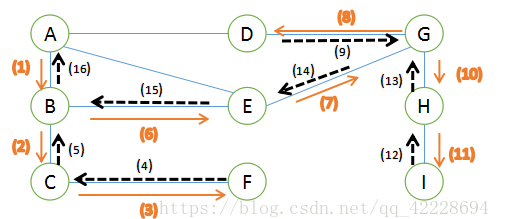
DFS.png

  1. //表结点
  2. struct ArcNode {
  3.     int adfvex;//表示该边的另外一个顶点在顶点表中的下标
  4.     ArcNode * next; //表示依附在该顶点的下一条边的信息
  5. };
  6. //头结点
  7. struct Vnode {
  8.     string data; //记录基本信息i
  9.     ArcNode * firstarc;//记录第一条依附在该顶点的边
  10. };
  11. //一个图的结构
  12. struct Graph_List {
  13.     int vexnum;  //图的顶点数
  14.     int edge;    //图的边数
  15.     Vnode * node;  //邻接表
  16. };
  18. //DFS遍历图
  19. void DFS_store_list(Graph_List g, int v, bool * & visit) {
  20.     cout << g.node[v].data << " ";
  21.     visit[v] = true;
  22.     ArcNode * next = g.node[v].firstarc;
  23.     while (next) {
  24.         if (!visit[next->adfvex]) {
  25.             DFS_store_list(g, next->adfvex, visit);//递归
  26.         }
  27.         else {
  28.             next = next->next;
  29.         }
  30.     }
  31. }
  33. void DFS_list(Graph_List g, int begin) {
  34.     int i;
  35.     bool * visit = new bool[g.vexnum];
  36.     for (i = 0; i < g.vexnum; i++) {
  37.         visit[i] = false;
  38.     }
  39.     DFS_store_list(g, 0, visit);
  40.     for (i = 1; i < g.vexnum; i++) {
  41.         if(!visit[i])
  42.             DFS_store_list(g, i, visit);
  43.     }
  44. }

2.BFS (Breadth First Search) 广度优先搜索

1任意点v出发=>访问v ->访问v的邻接点

2.v的邻接点出发 ->访问v的邻接点的邻接点

“先被访问的顶点的邻接点”先于”后被访问的邻接点”访问,直至图中所有的顶点都被访问到为止

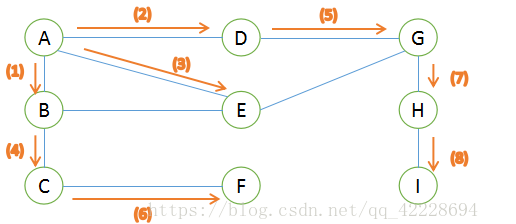
BFS.png

  1. //表结点
  2. struct ArcNode {
  3.     int adfvex;//表示该边的另外一个顶点在顶点表中的下标
  4.     ArcNode * next; //表示依附在该顶点的下一条边的信息
  5. };
  6. //头结点
  7. struct Vnode {
  8.     string data; //记录基本信息i
  9.     ArcNode * firstarc;//记录第一条依附在该顶点的边
  10. };
  11. //一个图的结构
  12. struct Graph_List {
  13.     int vexnum;  //图的顶点数
  14.     int edge;    //图的边数
  15.     Vnode * node;  //邻接表
  16. };
  17. //BFS遍历图
  18. void BFS_list(Graph_List g, int begin) {
  19.     int i;
  20.     bool * visit = new bool[g.vexnum];
  21.     for (i = 0; i < g.vexnum; i++) {
  22.         visit[i] = false;
  23.     }
  25.     queue<int>  q;
  26.     for (int v = 0; v < g.vexnum; v++) {
  27.         if (!visit[(begin + v) % g.vexnum])
  28.         {
  29.             cout << g.node[(begin - 1 + v) % g.vexnum].data << " ";
  30.             visit[(begin + v) % g.vexnum] = true;
  31.             q.push((begin + v) % g.vexnum);//初始化队列
  32.             while (!q.empty())
  33.             {
  34.                 int u = q.front();
  35.                 q.pop();
  36.                 ArcNode * next;
  37.                 next = g.node[u].firstarc;//获得依附在该顶点的第一条边的信息
  38.                 while (next) {//遍历该链表上的所有的点
  39.                     if (!visit[next->adfvex]) {
  40.                         cout << g.node[next->adfvex].data << " ";
  41.                         visit[next->adfvex] = true;
  42.                         q.push(next->adfvex);
  43.                     }
  44.                     next = next->next;
  45.                 }
  46.             }
  47.         }
  48.     }
  49. }