现代数字信号处理期末考试试卷解析

1.1 、（15分）设随机信号x(t) = Acos 0t + Bsin0t ，为正常数，A、B为相互独立的随机变量，且E(A) = E(B) = 0,D(A) = D(B) = 2 试证明x(t)是平稳随机信号。

1.2、 （15分）设随机信号x(t) = Acos 0t + Bsin0t ，为正常数，A、B为相互独立的随机变量，问满足什么条件下的是平稳随机信号？

和上题步骤一样，只是思考方式不一样。

2 、（15分）两个串联系统如图1所示。输入X(t)是广义平稳随机信号，自相关函数为R(T)，经过第一个系统函数ht)的系统输出为W(t)，在经过第二个系统函数h(t)的系统的输出为Y(t)，
（1）求W(t)的自相关函数以及W(t)和Y(t)的互相关函数R(t,t+T)
（2）试求X(t)和Y(t)的互相关函数.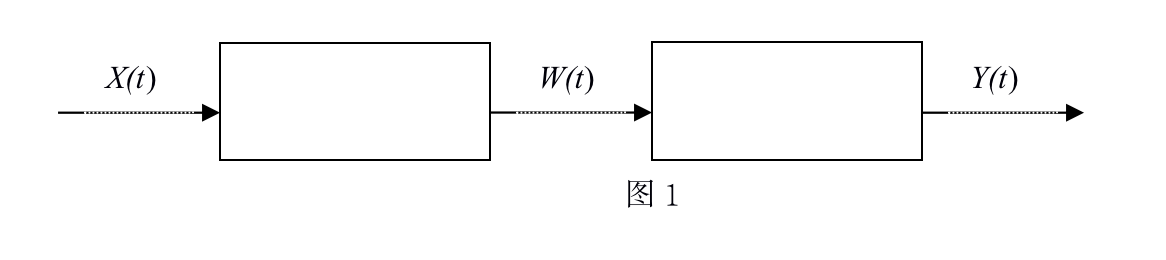

3、（10分）已知有理功率谱密度为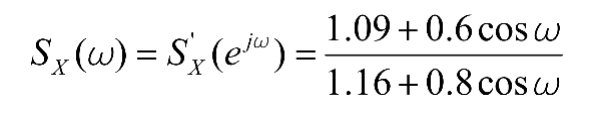求其模型系统函数。
以下答案中有一步写错了，就是根据分解结果应该是H（z） = C（z+ 0.3）/(z+0.4)
H（z）= C（z+ 0.3）/(z+0.4).答案中写反了，最后的系统函数应该是H（z） = （z-1+ 0.3）/(z-1+0.4)

4 、求功率谱密度为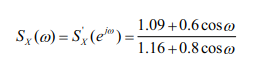的白化滤波器。

5 、(10分)设α，β为两个参数，已知x[0]= α+β+n，x[1]= α+n。其中n，n为均值为0，方差为σ的独立高斯随机变量。现在获得两次观测值x[0]=0，x[1]=1，用最大似然估计求α，β。

6、（15分）设x(n)是一个一次谐波过程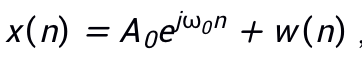，,w(n)为白噪声，已知x(n)的自相关矩阵为用特征分解谱估计求及w(n)的功率。
答案中少了一步求w(n)的功率。在此补充上
概念：w(n)是方差为2的白噪声。在自相关矩阵R进行特征分解中，2等于最小特征值。
所以以下的P(w(n)) = 2

7、（15分）假设有一实的广义平稳随机信号s(n)的自相关函数（序列）为rss(m) = 0.6,且伴随有实的噪声w(n)，方差为w2 = 1 ，与s(n)无关。试设计一个M=2的FIR维纳滤波器来估计s(n) ，并计算最小均方误差。

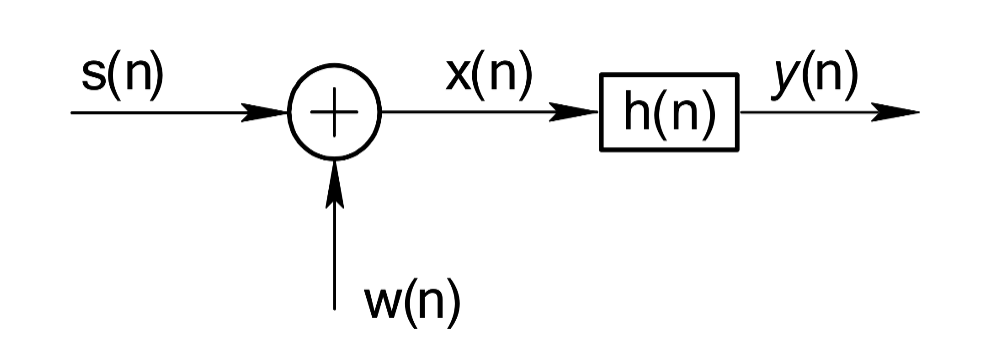
源PPT25页
https://wenku.baidu.com/view/5617d56bcaaedd3383c4d39e.html

8、（20分）已知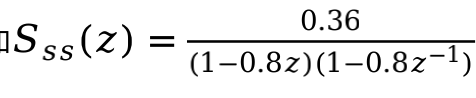，并且信号s(n)和噪声v(n)不相关，即rsv(m)=0，噪声v(n)是零均值、单位功率的白噪声（σ__v=1,mv=0)，求因果维纳滤波器的z域解H(z)和E［|e(n__)|］。
源PPT
https://wenku.baidu.com/view/b303579a001ca300a6c30c22590102020640f275.html?re=view