刷题

动态规划问题（求最值，求子序列）：

问题特征：

1. 具备最优子结构（能够将待求值转换为子结构问题）
2. 求解动态规划问题核心是高效率穷举
   • 保存子问题的解，从而避免重叠子问题
   • 备忘录dp
   • 高效率穷举——状态转移方程（子问题—>待求解问题）
3. 子问题之间相互独立（这样才具有最优子结构）
   • 以考试成绩为例
     • 如果语文数学成绩之间没有关系，这两门课成绩都考到最高就是总成绩最高
     • 如果语文高数学就要低，那么就不能说某一门成绩最高，总成绩就能最高

问题解决：

1. 如何思考状态转移方程：
   • 明确base case，就是初始值
   • 明确状态，在得到答案的过程中，有什么量是不断变化的, 一般状态就是dp数组的下标
   • 明确选择，不同的选择会导致不同的状态，什么样的选择可以得到最优子问题的解
   • 明确dp数组的定义， （一般是 dp[i]表示第i个。。。。最大/小的值）

一般动态规划框架(一般要求返回值是什么类型，数组就是什么类型)：

new dp;
//初始化 base case
dp[0][0][...] = base
//进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

状态压缩就是投影！该图片对应寻找最长回文子序列那道题，找base case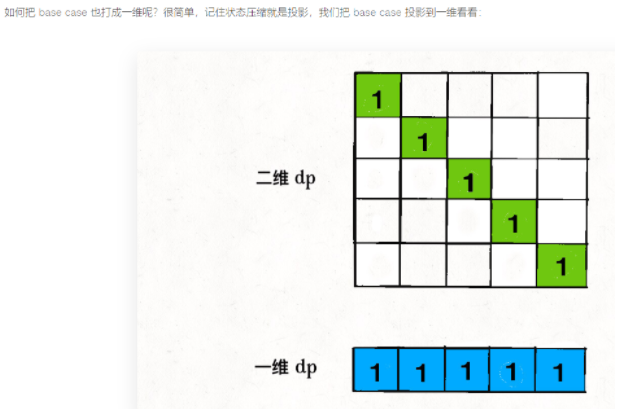

0-1背包问题

回溯算法/DFS（找出符合条件的全部值、全排列）

问题特征：

1. 本质上就是暴力穷举（有时候回溯也会超时）
2. 在暴力穷举的基础上，跳过重复值或者在不正确的路径上提前结束以剪枝

问题解决：

1. 路径：做出的选择（可以理解为已经选出来的一部分方案）
2. 选择列表：接下来要怎么走
3. 结束条件：符合的条件

代码框架：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

BFS（找最短距离，最少变化次数）

问题特征：

1. 在一副“图”中找最短距离
2. 不像dfs就往深扎，bfs是把自己能接触到得都先接触一遍（相当于学完一章知识之后一顿扩展，进行充份地复习），dfs是学完一章知识立马学习下一章，不复习

问题解决：

1. 核心数据结构是队列（队列每次存储的是上一个节点所能直接接触到的所有节点，就好比已经学完的那一章，书本后面的扩展阅读的所有内容）
2. 有时候如果要走回头路的可能（图结构是网状的，有时候一个没走过的点可能会连接了某个已经走过的点），还要建立一个visit列表，用来标记哪些节点已经走过了。
3. 一般让找最短距离，最少变化次数，所以要有个res，来记录这个最短的量。
   • 不像dfs，dfs的res有时候要用Math.max或者Math.min，那是因为他搜索地不充分，但bfs不一样，他每一次都搜索地很充分，只要找到了就是最小值。

代码框架：

int BFS(Node start, Node target){
    //核心结构队列，用来保存每一层的节点
    Deque<Node> deq;
    //若有往回走的可能，要整一个vis
    Set<Node> vis;
    //把起点放进队列
    deq.addLast(start);
    //标记起点已访问
    vis.add(start);
    //开始从start遍历
    while(!deq){
        int size = deq.size();
        //当前队列保存了上一层能联系到的所有节点，把这些节点一个个都poll出来一个一个查！
        for(int i = 0; i < size; i++) {
            Node cur = deq.poll();
            if (cur == target){
                return res;
            }
            //把cur能联系上的所有节点放到deq里面
            for (Node curNext : cur){
                if (vis.contains(curNext)) {  //只放没访问过得
                    deq.addLast(curNext);
                    vis.add(curNext);
                }  
            }
        }
        res++;
    }
    return 0 //没找到
}

二分查找（已经排序好了让查找，有重复数查找左右边界）

代码框架

//left 和 right分别是能够取到的左右边界
//这个是找左边界
int left = 0;
int right = nums.length - 1;
while(left <= right) { //因为是包含左右边界，所以带了等于
    int mid = left + (right - left) / 2;
    if (nums[mid] > target) right = mid - 1;
    else if (nums[mid] < target) left = mid + 1;
    //如果是找左边界就是right = mid - 1（锁定left），如果是找右边界就是left = mid + 1（锁定right）
    else right = mid - 1;
}
//最后还要判定是否出问题了，有可能数组里面没有target-->nums[left] != target，在找左边界的时候还有可能所有的数都小于target，这时left会超过数组范围。
if (left >= nums.length || nums[left] != target) return -1;
else return left;

//left 和 right分别是能够取到的左右边界
//这个是找右边界
int left = 0;
int right = nums.length - 1;
while(left <= right) { //因为是包含左右边界，所以带了等于
    int mid = left + (right - left) / 2;
    if (nums[mid] > target) right = mid - 1;
    else if (nums[mid] < target) left = mid + 1;
    //如果是找左边界就是right = mid - 1（锁定left），如果是找右边界就是left = mid + 1（锁定right）
    else left = mid + 1;
}
//最后还要判定是否出问题了，有可能数组里面没有target-->nums[left] != target，在找左边界的时候还有可能所有的数都小于target，这时left会超过数组范围。
if (right < 0 || nums[right] != target) return -1;
else return right;

滑动窗口（字符串相关）

问题解决

1. 类似于双指针，right指针维护窗口的后部，left指针维护窗口的前部
2. 字符串问题可以用map记录窗口中的内容
3. 本质就是维护一个窗口，不断往前滑动，滑动的同时更新map里面保存的窗口数据，同时更新最终答案

管你看没看懂，奥里给，直接上代码框架就完了！

//s是被匹配的串
public void slidingWindow(String s, String t) {
    HashMap<Character, Integer> window = new HashMap<>(); //保存窗口里面的数据
    int valid = 0; //  判断合法性，一般valid达到一定数量就要收缩窗口
    int left = 0; // 窗口的左边界
    int right = 0; //窗口的右边界
    while(right < s.size()) {
       //c是要移入窗口的字母
        char c = s.charAt(right);
          //右移窗口
        right++;
        //右移之后的操作（比如更新窗口数据，更新valid值等）
        /*debug可以在此处输出*/
        while(需要缩小窗口的条件) {
            //一般在此处更新最终结果值
            //d是要移出窗口的字母
            char d = s.charAt(left);
            //左移窗口
            left++;
            //左移窗口的一系列操作(比如更新窗口数据，更新valid值等)
        }
    }
}

买卖股票专题

问题特征：

1. 有没有手续费（选择的结果统一减去手续费）
2. 有没有冷冻期（天数）
3. 有没有限制（一共可以交易几次，几天呢可以交易几次）

问题解决：

1. 结合动态规划框架确定状态和选择：
   • 三种状态：天数、允许交易的最大次数、当前持有的状态（1表示持有，0表示没持有）
     • 例如dp 231,就表示在第二天，能交易3次的限制下，当前持有股票的最大收益，最终答案就是（dp 一共的天数 允许的交易次数 当前没持有股票的最大收益 ）
   • 三种选择：买入、卖出、不操作
2. 三种状态对应dp是几维的
3. 三种选择每次选取最优的

代码框架：

int[][][] dp = new int[天数][最大交易次数][2];
dp[i][0][0] = 0;  //没有买入，当前利润是0
dp[i][0][1] = -prices[0];  //第一天如果持有股票，当前利润就是-prices[0]
//当前没有持有股票，有两种可能，一个是保持了昨天没有持有股票的状态，另一个是昨天持有股票，今天给卖了
dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + price[i]);
//当前持有股票，两种可能，一种是保持了昨天持有股票的状态，另一种是昨天没持有股票，今天买入了。  注意每次买入股票要损失一次交易机会，所以应该在昨天且交易机会有k-1次的情况下计算。
dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - price[i]);

递归（二叉树问题）

问题解决：

1. （这个函数是干嘛得）明确定义的函数是什么，相信这个定义，利用这个定义推到最终结果
2. 这个函数参数中得变量是什么
3. 得到函数得递归结果用来做什么

二叉树递归框架：

//前序遍历
void BST(TreeNode root) {
    doSomething();
    BST(root.left);
    BST(root.right);
}
//中序遍历
void BST(TreeNode root) { 
    BST(root.left);
    doSomething();
    BST(root.right);
}
//后序遍历
void BST(TreeNode root) {    
    BST(root.left);
    BST(root.right);
    doSomething();
}

二叉搜索树递归框架：

void BST(TreeNode root, int target) {
    if (root.val == target)  doSomething();
    else if (root.val > target) BST(root.left, target);
    else BST(root.right, target);
}

判断二叉搜索树合法性：

void BFS(TreeNode root, TreeNode max, TreeNode min) {
    if (root == null) return true;
    if (min != null && root.val <= min.val) return false;
    else if (max != null && root.val >= max.val) return false;
    return BFS(root.left, r)
}

图

问题解决：

1. 逻辑结构：由节点和边构成
2. 表达形式：邻接表和邻接矩阵
   • 邻接表：把每个节点x的邻居都存在一个列表里面，然后把x与这个列表关联起来
     • 占用内存小
   • 邻接矩阵：matrix [x] [y]，如果xy相连，就把matrix[x] [y]设为true，想找x的邻接节点，扫描matrix[x] 行即可。
     • 查找快

图的遍历代码框架：

boolean[] vis; //如果含有环结构，要记录哪些已经访问过了
void traverse(Graph graph, int s) {
    //图的加入和移除要放在for外面，否则会漏掉起始点的遍历
    if (vis[s]) return;
    for (int neighbor : graph.neighbors(s)) {
        traverse(graph, neighbor);
    }
    vis[s] = false;
}

算法技巧

前缀和（可以应用于数组和树，求连续的几个节点的和为某个值）

力扣560 和 437

//map的键为前缀的大小，值为该前缀出现的次数，且map是随着遍历的进行不断丰富的（否则会不是连续的）
HashMap<Integer, Integer>() map = new HashMap<>();
//连续的从i到j的和计算方式为  pre[j + 1] - pre[i],从字典查找pre[j - 1] - k出现过的次数即可。可以用sum0_i变量作为pre[j + 1]。 sum0_j为要查询的数。
树也一样，但要注意树的前缀和不但要加还要减，因为有些节点不在一条s

题目出现只包含26个小写字母

第一时间想到 int[] count = new int[26]

计数质数

（搞一个Boolean数组记录是不是质数，先全都置为质数，不断把质数的倍数置为合数，计算质数的数量）

class Solution {
    public int countPrimes(int n) {
        boolean[] arrs = new boolean[n];
        Arrays.fill(arrs, true); //全部初始化为质数
        int res = 0;
        for (int i = 2; i * i < n; i++) {
            if (arrs[i]) {
                int x = i;
                while(x*i < n && x*i > 0) {
                    arrs[x*i] = false;
                    x++;
                }
            }
        }
        for (int i = 2; i < n; i++) {
            if (arrs[i]) res++;
        }
        return res;
    }
}

快速幂求余

//x是底数，a是幂，p是余数
注意x和res都是long类型的
public long remainder(long x, int a, int p) {
        long res = 1;
        while(a > 0) {
            if (a % 2 != 0) res = (res * x) % p;
            x = x * x % p;
            a /= 2;
        }
        return res;
    }

有限状态自动机

有限状态自动机是一类计算模型，它包含一系列状态，这些状态中：

• 有一个特殊的状态，被称作初始状态
• 还有一系列状态被称为接受状态，它们组成了一个特殊的集合。其中，一个状态可能既是初始状态，也是接受状态。

1. 起初，自动机处于初始状态，随后，它顺序地读取字符串中的每一个字符，并根据当前状态和读入的字符，按照某个事先约定好的转移规则，从当前状态转移到下一个状态。
2. 当状态转移完成后，它读取下一个字符，当字符串全部读取完毕后，如果自动机处于接受状态，则判定该字符串被接受，否则被拒绝
   • 如果转移过程中发生了转移失败的情况（不存在对应的转移规则），此时会终止转移，并判定被拒绝

常见时间复杂度对应的算法

O(1)

一般都是数学方法或者找规律直接求解的方法

O(logn)

二分法或者位运算

O(n^0.5)

分解质因数

O(n)

一般都是循环一遍（或者两遍）得到解，简单的链表或者数组的题大都是O(n)

可能的算法有

• 枚举
• 一维状态动态规划
• 树、图遍历算法，包括并查集
• 可能用到栈和队列
• 哈希表
• 双指针
• 贪心
• 二分查找

O(nlogn)

• 排序，可能数据排序以后可以很容易解决
• 可能用到优先队列，比如用到堆
• 多次二分检索的问题
• 分治算法
• 可能用到线段树或者其他的高级数据结构

O(n^2)

一般就是两重循环

• 动态规划
• 枚举
• 数组

排序

1. 快速排序
2. 归并排序
3. 堆排序
4. 桶排序
5. 计数排序
6. 归并排序
7. 基数排序