1.0 样本空间和随机事件

此门学科研究 随机现象 的 统计规律性。
统计规律性：在大量重复试验中，呈现出的固有规律性。如重复抛硬币。
随机现象：单次试验中结果呈现不确定性，大量重复试验中结果又具有统计规律性的现象。

样本空间

随机试验的可能结果集合。
掷硬币的样本空间为 {正，反}
掷骰子的样本空间为 {1,2,3,4,5,6}
城市发生交通事故的次数，样本空间为 {0,1,2,3,4,5,6….}

如何计算样本空间？

掷硬币，基本事件是 2，抛 3 次，则样本空间 = 2 = 2×2×2 = 8；抛 10 次，则样本空间 = 210

随机事件

事件是样本空间的子集，掷骰子有 6 个基本事件：{1},{2},{3},{4},{5},{6}
事件的关系：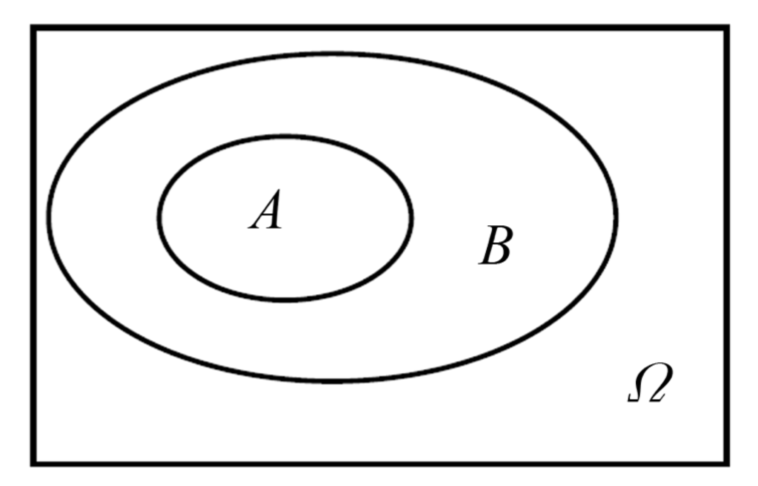
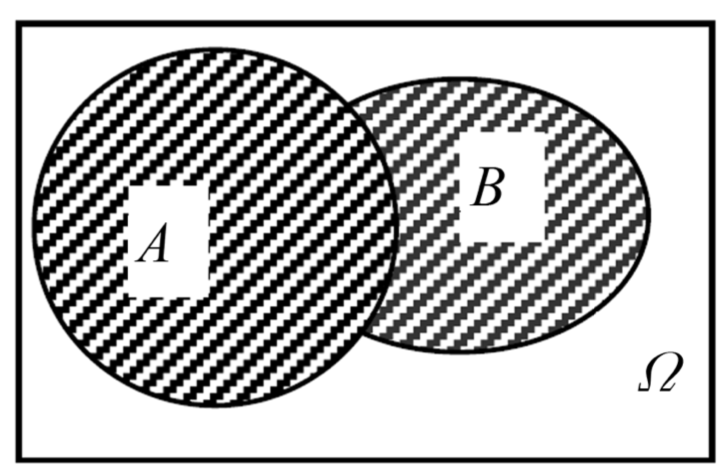
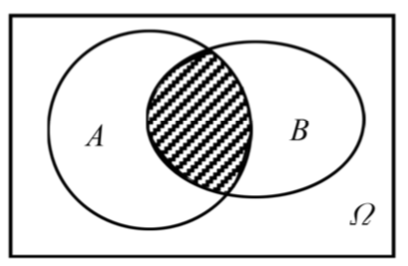
或
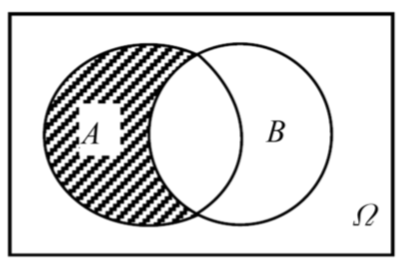
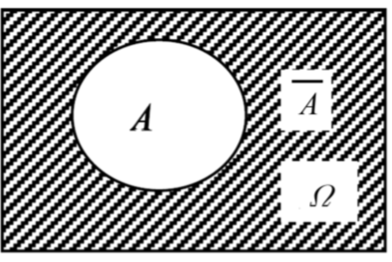
逆事件
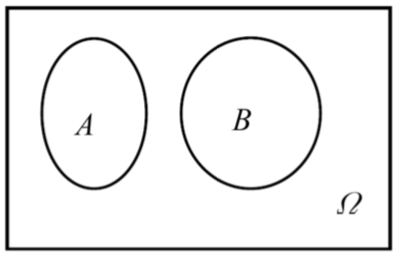
A 与 B 不相容或互斥

交换律：
结合律：
分配率：
对偶律(De Morgan 律)：
对于多个随机事件, 上述运算律也成立。

此外还有
吸收率：
重余律：
幂等律：
差化积： 不理解的话看看图

常见例子

A 和 B 至少有一个发生：
A 和 B 同时发生：

表示 A 和 B 不同时发生
表示 A 和 B 都不发生，两者是不一样的
两者的联系是