数据结构_左右栈

907. 子数组的最小值之和

题解： https://leetcode.cn/problems/sum-of-subarray-minimums/solution/xiao-bai-lang-dong-hua-xiang-jie-bao-zhe-489q/

方案一：单调栈+贡献值

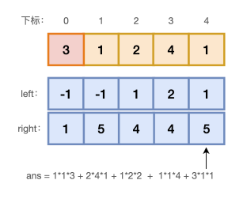
function sumSubarrayMins(arr: number[]): number {
  const n = arr.length;
  let left = new Array(n).fill(-1);
  let right = new Array(n).fill(n);
  let stack = [];
  // left
  for (let i = 0; i < n; i++) {
    while (stack.length && arr[stack[0]] > arr[i]) {
      stack.shift();
    }
    left[i] = stack.length ? stack[0] : -1;
    stack.unshift(i);
  }
  stack = [];
  // right
  for (let i = n - 1; i >= 0; i--) {
    while (stack.length && arr[stack[0]] >= arr[i]) {
      stack.shift();
    }
    right[i] = stack.length ? stack[0] : n;
    stack.unshift(i);
  }
  // console.log(left, right)
  // 每个范围的贡献
  let ans = 0;
  const mod = 10 ** 9 + 7;
  for (let i = 0; i < n; i++) {
    ans = (ans + arr[i] * (i - left[i]) * (right[i] - i)) % mod;
  }
  return ans;
};

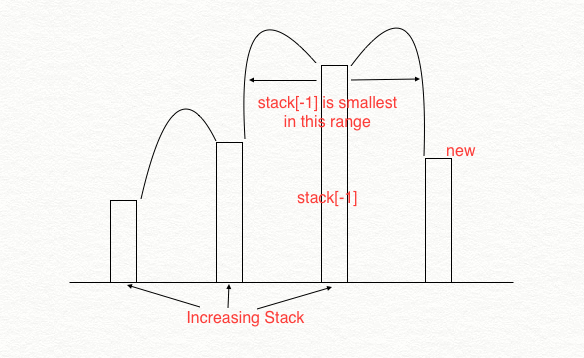
方案二： 维护一个“递增”stack

function sumSubarrayMins(arr: number[]): number {
    const n = arr.length;
    function getEle(i: number): number {
        if (i == -1 || i == n) return Number.MIN_SAFE_INTEGER;
        return arr[i];
    }
    let ans = 0;
    const mod = 10 ** 9 + 7;
    let stack = [];
    for (let i = -1; i <= n; i++) {
        while (stack.length && getEle(stack[0]) > getEle(i)) {
            const idx = stack.shift();
            ans = (ans + arr[idx] * (idx - stack[0]) * (i - idx)) % mod;
        }
        stack.unshift(i);
    }
    return ans;
};

进一步优化 :::info 数组中每个元素 E = arr[i] 作为最小值的范围 (L, R) ，子数组个数为 count = (i - L) (R - i )，元素 E 的总贡献值为 arr[i] count。计算出每个元素的贡献值，然后求和。
利用单调栈 q，找出 arr[q[-1]] 作为最小值的范围，即 (q[-2], i) ， Subarray 个数，分两步 左 i - j 个选择，右 j - q[-1] 个选择。 :::

function sumSubarrayMins(arr: number[]): number {
    arr.push(-1);
    const n = arr.length;
    let ans = 0;
    const mod = 10 ** 9 + 7;
    let stack = [-1];
    for (let i = 0; i < n; i++) {
        while (stack.length && arr[i] < arr[stack[0]]) {
            const j = stack.shift();
            ans = (ans + arr[j] * (j - stack[0]) * (i - j)) % mod;
        }
        stack.unshift(i);
    }
    return ans;
};