背包问题:
0-1背包问题(物品个数有且仅有一个)
问题描述:
有一个背包,他的容量为C(Capacity)。现在有n中不同的物品,编号为0…n-1,其中每一件物品的重量为w(i),价值为v(i)。问可以向这个背包中盛放哪些物品,使得在不超过背包容量的基础上,物品的总价值最大。
举例1:
N=5, C = 10, w = [2,2,6,5,4], v = [6,3,5,4,6]
0: (5) [0, 0, 0, 0, 0]1: (5) [0, 0, 4, 4, 4]2: (5) [0, 2, 4, 6, 6]3: (5) [0, 2, 4, 6, 6]
分析:
dp存放当前价值最大值。
F(n,C)考虑将n个物品放进容量为C的背包,使得价值最大。
- 0 , 不选, F(n-1, C)
- 1, 选, F(n-1, C - w(i)) + v(i)
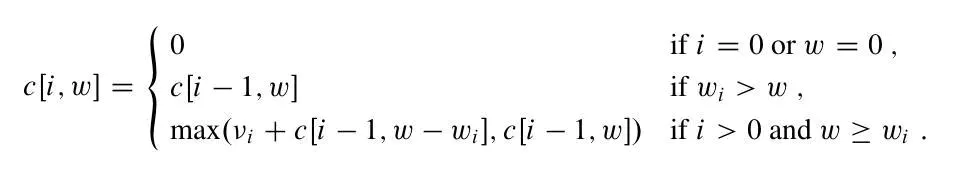
状态转移方程
for i in [1-n]: // 枚举物品
for j in [1-c]: // 枚举体积
if j - w[i] >= 0: // 放置
dp[i][j] = max{dp[i-1][j], dp[i-1][j-w[i]] + v[i]}
else: // 不放置
dp[i][j] = dp[i-1][j]
return dp[n][c]
初始化
枚举体积前, 背包为空, 故第一行全为0
枚举物品前, 故第一列全为0
0 0 0 0
0 X X X
0 X X X
复杂度
时间/空间均为O(nc)
完整实现
console.log(pack01(5, 10, [2,2,6,5,4], [6,3,5,4,6])); // 15
console.log(pack01(3, 4, [2,1,3], [4,2,3])); // 6
function pack01(n, c, w, v) {
let dp = Array.from({ length: n+1}, (v, i) => new Array(c+1).fill(i == 0 ? 0 : null));
for (let i=1; i <= n; i++) {
dp[i][0] = 0;
}
for (let i=1; i<=n; i++) {
for (let j=1; j<=c; j++) {
let curW = w[i-1], curV = v[i-1]
if (curW > j) {
dp[i][j] = dp[i-1][j]
} else {
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-curW]+curV)
}
}
}
// console.log(dp)
return dp[n][c];
}
优化(降维):
dp[i][j] 降维成 dp[j], 第i个物品的j价值转为更新j价值
dp[j] = max{dp[j], dp[j-w[i]+v[i]]}
状态转移
for i in [1-n]:
for j in [c-j]:
dp[j] = max{dp[j], dp[j-w[i]]+v[i]}
return dp[c]
初始化
选物品前, 体积均为最大值是0
dp = new Array(j).fill(0)
复杂度
时间复杂度O(nc), 空间复杂度降为O(c)
举例
pack01(3, 4, [2,1,3], [4,2,3])
i=0 [0, 0, 0, 0, 0]
i=1 [0, 0, 4, 4, 4]
i=2 [0, 2, 4, 6, 6]
i=3 [0, 2, 4, 6, 6]
i=4 [0, 2, 4, 6, 6]
完整实现
console.log(pack01(5, 10, [2,2,6,5,4], [6,3,5,4,6])); // 15
console.log(pack01(3, 4, [2,1,3], [4,2,3])); // 6
function pack01(n, c, w, v) {
let dp = new Array(c+1).fill(0);
for (let i=1; i<=n; i++) {
let curW = w[i-1], curV = v[i-1];
for (let j=c; j>=curW; j--) {
dp[j] = Math.max(dp[j], dp[j-curW]+curV);
}
}
// console.log(dp)
return dp[c];
}
416. 分割等和子集
例子:
[2,2,3,5] // false
474. 一和零
494. 目标和
377. 组合总和 Ⅳ
2291. Maximum Profit From Trading Stocks
function maximumProfit(present: number[], future: number[], budget: number): number {
let packet = present.map((v, i) => [v, future[i] - v]);
let dp = new Array(budget + 1).fill(0);
for (let [v, w] of packet) {
for (let j = budget; j >= v; j--) {
dp[j] = Math.max(dp[j], dp[j - v] + w);
}
}
return dp[budget];
};
完全背包问题(物品个数不限)
面试题 08.11. 硬币
function waysToChange(n: number): number {
const MOD = 10 ** 9 + 7;
let coins = [1, 5, 10, 25];
let dp = new Array(n + 1).fill(0);
dp[0] = 1;
for (let coin of coins) {
for (let i = coin; i <= n; ++i) {
dp[i] += dp[i - coin];
}
}
return dp.pop() % MOD;
};
518. 零钱兑换 II
function change(amount: number, coins: number[]): number {
let dp = new Array(amount + 1).fill(0);
dp[0] = 1;
for (let coin of coins) {
for (let i = coin; i <= amount; ++i) {
dp[i] += dp[i - coin];
}
}
return dp.pop();
};
322. 零钱兑换
function coinChange(coins: number[], amount: number): number {
let dp = new Array(amount+1).fill(amount+1);
dp[0] = 0;
for (let coin of coins) {
for (let i = coin; i <= amount; ++i) {
dp[i] = Math.min(dp[i], dp[i-coin] + 1);
}
}
let res = dp.pop();
return res > amount ? -1 : res;
};
多重背包问题(物品个数存量不同)
背包问题九讲
算法小抄-背包问题
https://mp.weixin.qq.com/s/FwIiPPmR18_AJO5eiidT6w

