图论基本概念（一）

saltriver 2017-01-14 20:47:37 92197
分类专栏： 数据结构与算法 文章标签： 数据结构 图
版权
图（graph）是数据结构和算法学中最强大的框架之一（或许没有之一）。图几乎可以用来表现所有类型的结构或系统，从交通网络到通信网络，从下棋游戏到最优流程，从任务分配到人际交互网络，图都有广阔的用武之地。

通常来说，我们会把图视为一种由“顶点”组成的抽象网络，网络中的各顶点可以通过“边”实现彼此的连接，表示两顶点有关联。注意上面图定义中的两个关键字，由此得到我们最基础最基本的2个概念，顶点（vertex）和边（edge）。直接上图吧。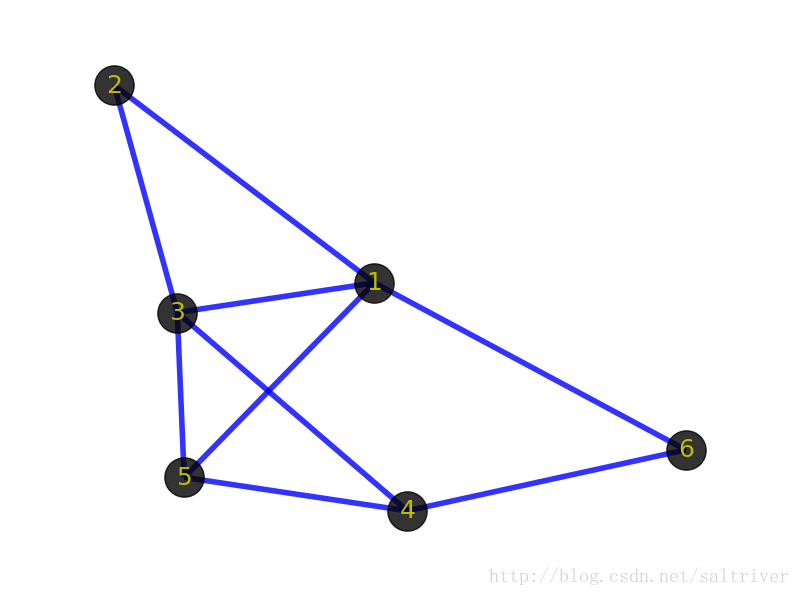

一、顶点（vertex）

上图中黑色的带数字的点就是顶点，表示某个事物或对象。由于图的术语没有标准化，因此，称顶点为点、节点、结点、端点等都是可以的。叫什么无所谓，理解是什么才是关键。

二、边（edge）

上图中顶点之间蓝色的线条就是边，表示事物与事物之间的关系。需要注意的是边表示的是顶点之间的逻辑关系，粗细长短都无所谓的。包括上面的顶点也一样，表示逻辑事物或对象，画的时候大小形状都无所谓。

三、同构（Isomorphism ）

先看看下面2张图：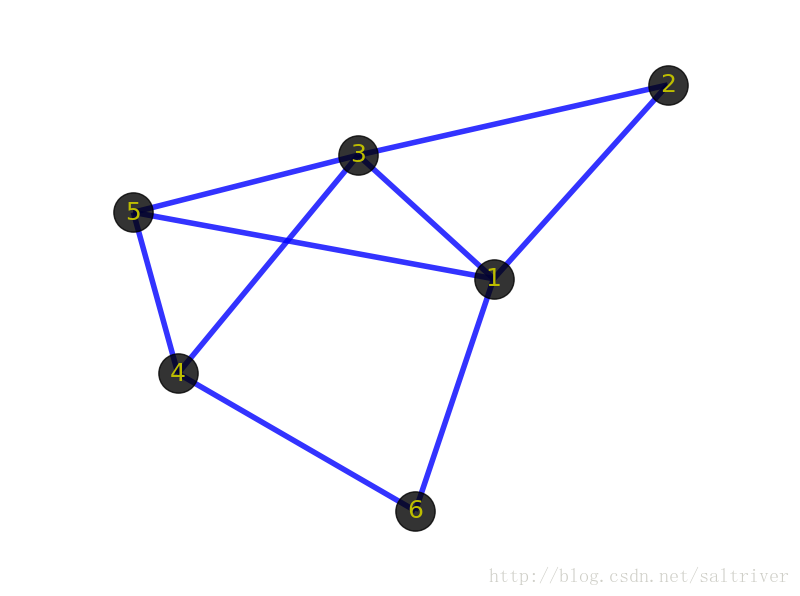

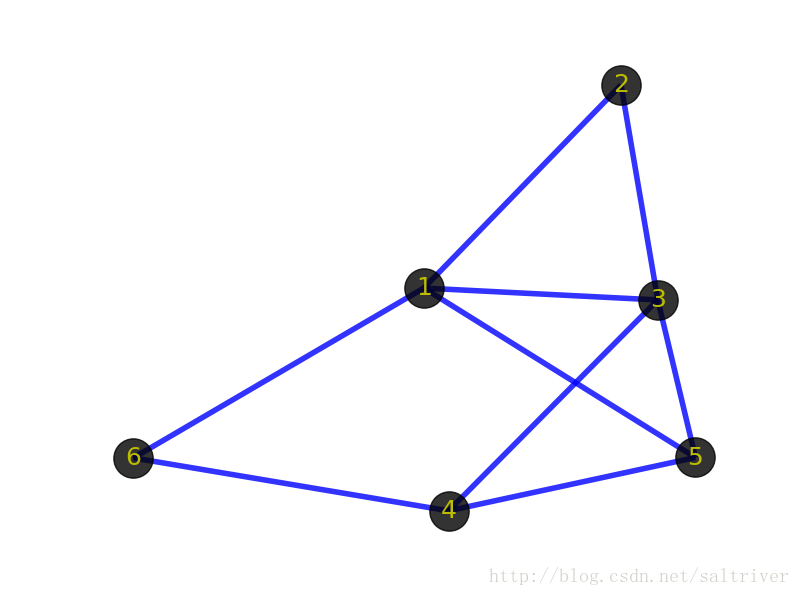
首先你的感觉是这2个图肯定不一样。但从图（graph）的角度出发，这2个图是一样的，即它们是同构的。只要不改变顶点代表的事物本身，不改变顶点之间的逻辑关系，那么就代表这些图拥有相同的信息，是同一个图。同构的图区别仅在于画法不同。

四、有向/无向图（Directed Graph/ Undirected Graph）

最基本的图通常被定义为“无向图”，与之对应的则被称为“有向图”。两者唯一的区别在于，有向图中的边是有方向性的。下图即是一个有向图，边的方向分别是：(1->2), (1-> 3), (3-> 1), (1->5), (2->3), (3->4), (3->5), (4->5), (1->6), (4->6)。要注意，图中的边(1->3)和(3->1)是不同的。有向图和无向图的许多原理和算法是相通的。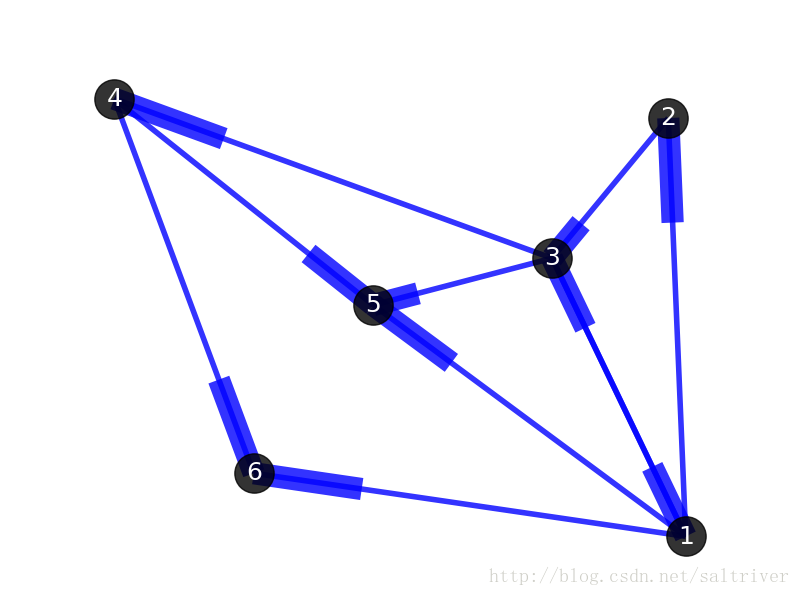

五、权重（weight）

边的权重（或者称为权值、开销、长度等），也是一个非常核心的概念，即每条边都有与之对应的值。例如当顶点代表某些物理地点时，两个顶点间边的权重可以设置为路网中的开车距离。下图中顶点为4个城市:Beijing, Shanghai, Wuhan, Guangzhou，边的权重设置为2城市之间的开车距离。有时候为了应对特殊情况，边的权重可以是零或者负数，也别忘了“图”是用来记录关联的东西，并不是真正的地图。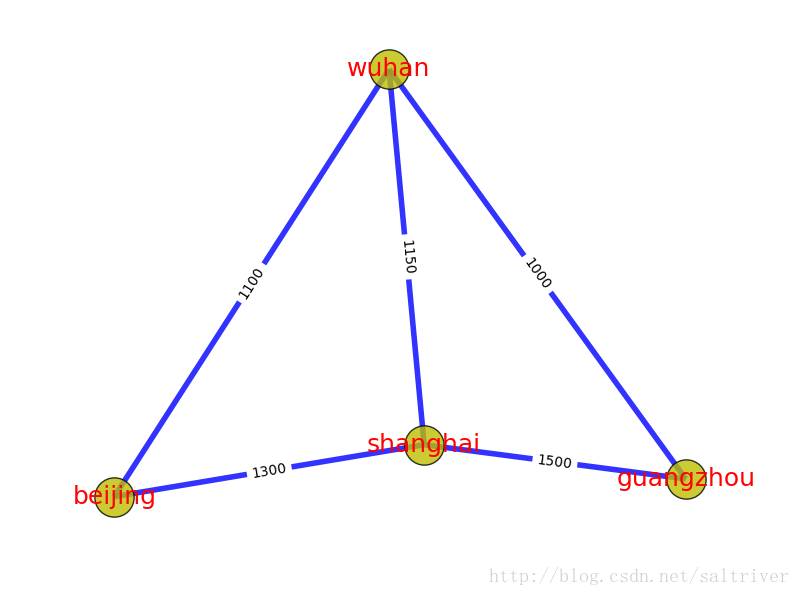

六、路径/最短路径（path/shortest path）

在图上任取两顶点，分别作为起点（start vertex）和终点（end vertex），我们可以规划许多条由起点到终点的路线。不会来来回回绕圈子、不会重复经过同一个点和同一条边的路线，就是一条“路径”。两点之间存在路径，则称这2个顶点是连通的（connected）。
还是上图的例子，北京->上海->广州，是一条路径，北京->武汉->广州，是另一条路径，北京—>武汉->上海->广州，也是一条路径。而北京->武汉->广州这条路径最短，称为最短路径。
路径也有权重。路径经过的每一条边，沿路加权重，权重总和就是路径的权重（通常只加边的权重，而不考虑顶点的权重）。在路网中，路径的权重，可以想象成路径的总长度。在有向图中，路径还必须跟随边的方向。
值得注意的是，一条路径包含了顶点和边，因此路径本身也构成了图结构，只不过是一种特殊的图结构。

七、环（loop）

环，也成为环路，是一个与路径相似的概念。在路径的终点添加一条指向起点的边，就构成一条环路。通俗点说就是绕圈。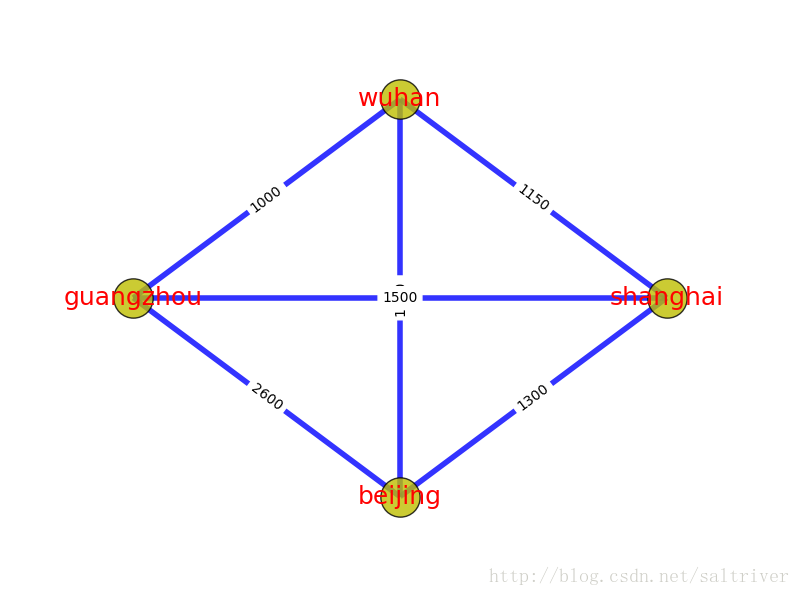

上图中，北京->上海->武汉->广州->北京，就是一个环路。北京->武汉->上海->北京，也是一个环路。与路径一样，有向图中的环路也必须跟随边的方向。环本身也是一种特殊的图结构。

八、连通图/连通分量（connected graph/connected component）

如果在图G中，任意2个顶点之间都存在路径，那么称G为连通图（注意是任意2顶点）。上面那张城市之间的图，每个城市之间都有路径，因此是连通图。而下面这张图中，顶点8和顶点2之间就不存在路径，因此下图不是一个连通图，当然该图中还有很多顶点之间不存在路径。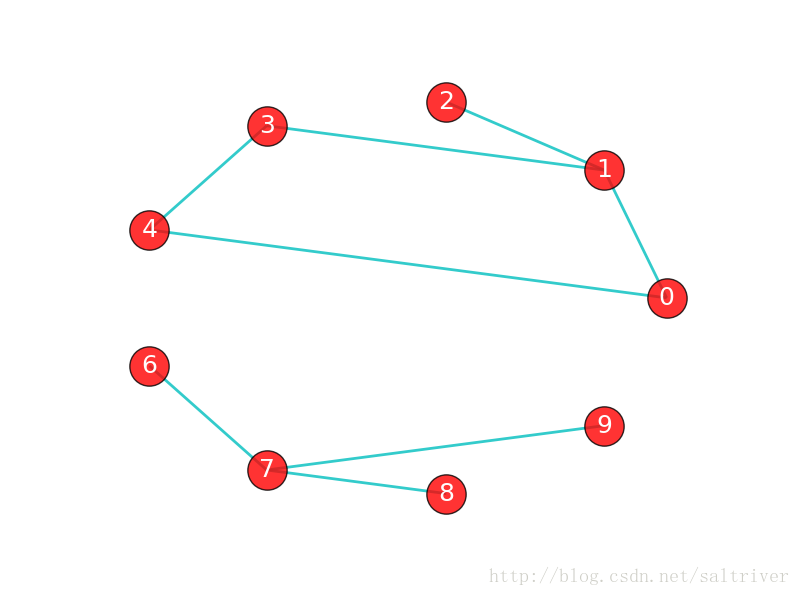

上图虽然不是一个连通图，但它有多个连通子图：0,1,2顶点构成一个连通子图，0,1,2,3,4顶点构成的子图是连通图，6,7,8,9顶点构成的子图也是连通图，当然还有很多子图。我们把一个图的最大连通子图称为它的连通分量。0,1,2,3,4顶点构成的子图就是该图的最大连通子图，也就是连通分量。
连通分量有如下特点：
1）是子图；
2）子图是连通的；
3）子图含有最大顶点数。
注意：“最大连通子图”指的是无法再扩展了，不能包含更多顶点和边的子图。0,1,2,3,4顶点构成的子图已经无法再扩展了。
显然，对于连通图来说，它的最大连通子图就是其本身，连通分量也是其本身。
你是不是已经对没完没了的术语感到厌烦了。是的，不能再多了！有了这些，我们可以出发探索图论的世界了！

图论（二）树

saltriver 2017-01-14 20:55:34 15040
分类专栏： 数据结构与算法 文章标签： 数据结构 树
版权
建立了图（graph）的认识，“树”就好理解了。“树”是一种很特别的图（graph）。用图来定义“树”：任意2点之间都连通，并且没有“环”的图。下面的图就是一颗树，因此，树是图的特例。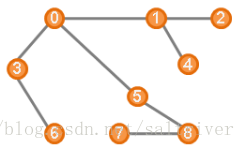

当然，由于树是一种特别有用的数据结构，因此，它有着一些自身的特点和概念：

一、节点（node）

就是图（graph）的顶点（vertex）。如上图中的顶点：0,1,2,3,4,5,6,7,8。

二、枝（branch）

就是图（graph）的边（edge）。如上图中的0->1, 0->3, 0->5, 1->2, 1->4, 3->6, 5->8, 8->7。

三、根（root）

一颗树可以想象成从某一个顶点开始进行分枝，那么这个顶点就是“根”。一颗树的每一个节点都可以作为根。如图中可以将节点0作为根。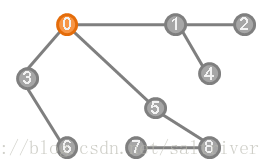

四、叶（leaf）

在一颗树上选定根后，如节点0作为根。由根开始不断分枝，途中所有无法再分枝的节点成为叶。如下图中，根为点0，则节点2,4,6,7是叶。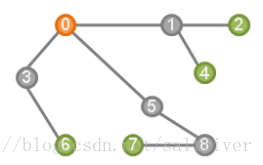

五、度（degree）

一个节点拥有的子树数称为节点的度(degree)。下图中，根节点0有3个子树，度为3；节点1有2个子树，度为2；节点3,5分别只有一个子树，度为1。叶(leaf)也可以用度来定义：度为0的节点称为叶(leaf)。节点2,4,6,7没有子树，度为0，所以2,4,5,7为叶。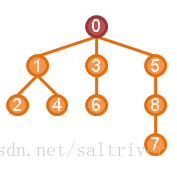

六、层/深度/高度（level/depth/height）

在一颗树中选定根（root）后，按照每个点离根的距离，可以将树中的点分为多个层级。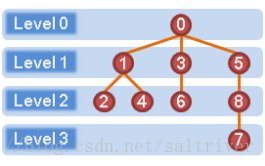

而一个树的最大层级数称为树的深度（depth）或高度(height)，如该树的深度(高度)为4。一个节点到下方的叶的最大层级数之差称为节点的高度（height），如节点1位于层1，下方的叶子2,4位于层2，所以节点1的高度是1；同理，节点3的高度也是1，节点5的高度是2，节点2本身是叶，其高度是0，根节点0的高度是3。

七、双亲/孩子/兄弟（parent/child/sibling）

在一颗树中选定根（root）后，相邻的两点，靠近根的是双亲（parent），远一点的是孩子（child）。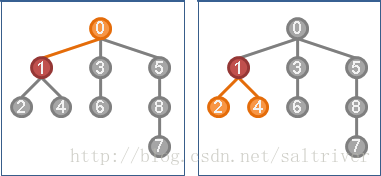

如上图中，0是1的双亲(parent)，2,4是1的孩子(child)。2，4有共同的双亲，因此2,4之间互称为兄弟（sibling）。
同样的，3是6的双亲，6是3的孩子；5是8的双亲，8是5的孩子。1,3,5是0的孩子，1,3,5互称为兄弟。

八、祖先/后代（ancestor/descendant）

在一颗树中选定根（root）后，一个点的双亲、双亲的双亲、……都是此点的祖先(ancestor)，根节点是所有子节点的祖先，注意双亲(parent)也属于祖先。因此，祖先是一个集合概念。同理，一个点的孩子、孩子的孩子、……都是此点的后代(descendant)，后代也是一个集合概念。

九、森林（forest）

很多颗树的集合称为森林。森林中，树与树之间互不相交。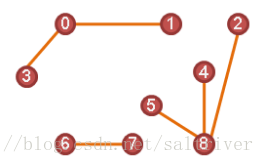

此外，与图一样，树也有“有向/无向”，“同构”，“权重”，“路径”等概念，含义与图类似，不再赘述。
最后总结下：
1.树中所有点都是连通的；
2.树中任意2点之间只有唯一一条路径；
3.树是无环的连通图；
4.森林是无环的非连通图。

图论（三）图的遍历

saltriver 2017-01-14 21:03:01 13570
分类专栏： 数据结构与算法 文章标签： 遍历 搜索 数据结构
版权
图建构好后，针对具体的问题，我们常常需要通盘的读取图中的信息，包括顶点（vertex）和边（edge），以及它们之间的关系。这种读取图中所有信息的方法就是图的遍历（traversal），也称为搜索（search），就是从图中某个顶点出发，沿着一些边访问图中所有的顶点，且使每个顶点仅被访问一次。遍历是很多图论算法的基础。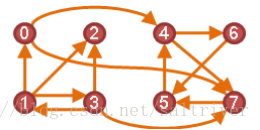

遍历需要决定从哪里开始读，依照什么顺序读，要读到哪里为止。如果遍历方法与需解决问题结合的好，甚至还可以一边读取图的信息，一边顺手解决问题！

（1）图和树的遍历

树的遍历是从根节点开始的，由于每个节点都只有一个双亲，因此其遍历还是相对简单的。而图的遍历则可以选择从任意一个节点开始，同时图中每一个节点都可能与其余的节点相邻接，不可避免的会多次访问同一个节点，因此在遍历的过程中需要将已访问的节点打上标记，以避免重复。

（2）遍历的方法

遍历有2个著名的方法：深度优先搜索（DFS, depth first search）和宽度优先搜索（BFS, breadth first search）。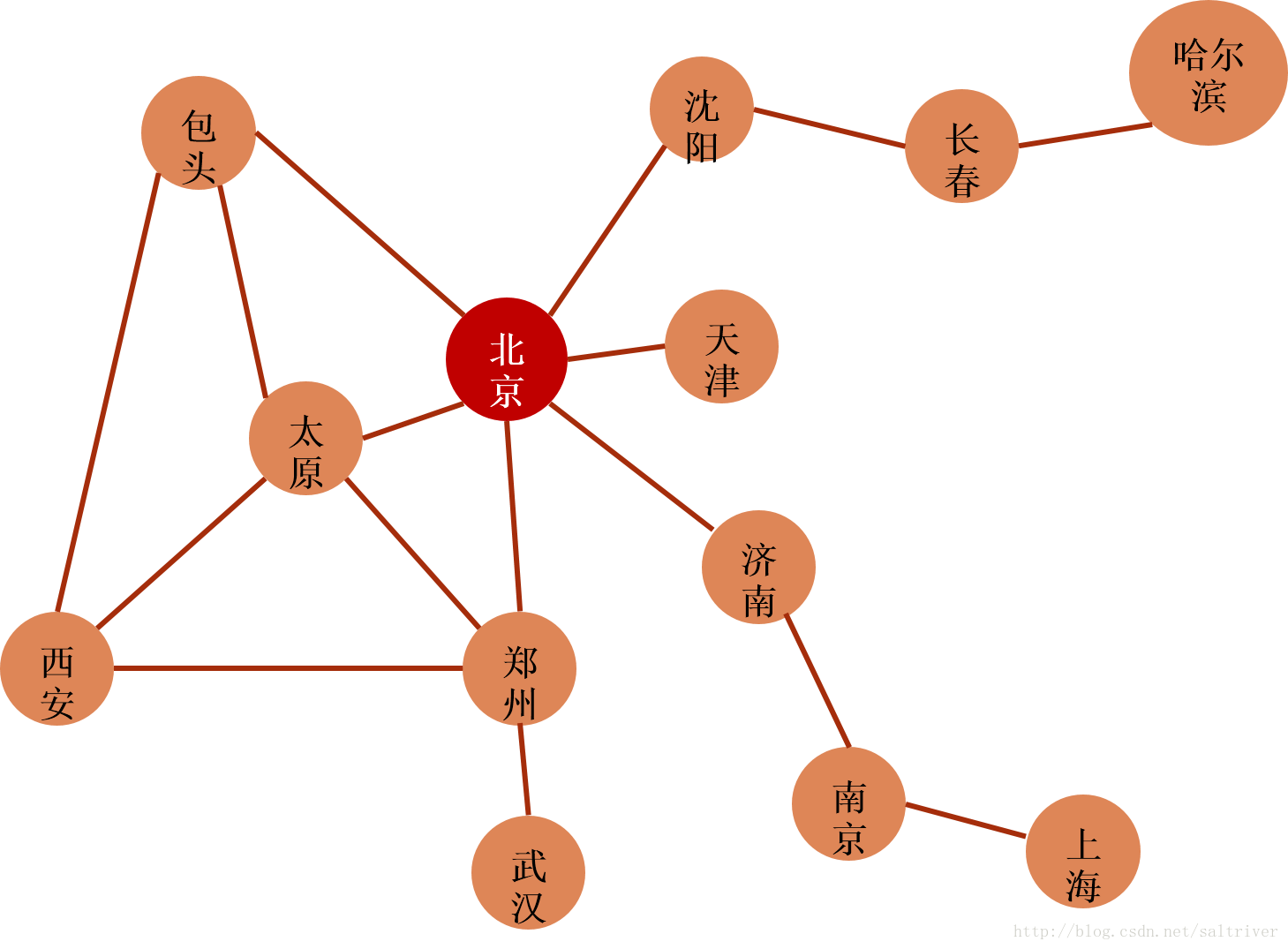

以上图的中国公路网为例，我们从北京出发，采用怎样的遍历方法访问所有的城市呢？
宽度优先就是从北京出发，先访问那些直接与北京相连的城市，比如天津、沈阳、包头、太原、郑州、济南等；然后再访问那些城市和这些已访问过的城市相连，如长春与沈阳相连，武汉与郑州相连，南京与济南相连等。而后再访问与长春、武汉、南京等相连的城市，如哈尔滨、上海等，直到把所有的城市都访问一遍为止。

深度优先就是从北京出发，随便找一个相连的城市，如济南，作为访问的城市，然后从济南出发，随便找一个与济南相连的城市，比如南京，再从南京出发，随便找一个与南京相连的城市，如上海，一直找到头，直到找不到城市，再往回找。因为一条路“走到黑”，所以叫深度优先。
这两种方法都可以保证访问到全部的城市。当然，前面也提到过，不论采用何种方法，都应该记录下已访问的城市，避免重复访问或遗漏。
深度优先和广度优先分别使用了stack和queue两种数据结构，得到了不同的遍历顺序。这个以后再分别详细介绍它们的工作原理和具体方法。

（3）遍历的时间复杂度

关于图遍历的时间复杂度。对于一个图来说，不管我们使用什么样的图存储结构和搜索方法，该图中的各个顶点(vertex)和各条边(edge)都是必须要搜索到的。因此，遍历一个图的时间复杂度至少是O(V+E)级别的，V,E分别表示顶点和边的数量。
当然，这里的遍历指的是用来访问图中每个节点的。但有时候，我们其实只需要寻找某个特定节点或某一类节点，对于这种搜索，我们也可以通过设计高效的算法来大大提高搜索效率。

图论（四）宽度优先搜索BFS

saltriver 2017-01-14 21:22:04 7786
分类专栏： 数据结构与算法 文章标签： 搜索 遍历 数据结构与算法 bfs
版权
宽度优先搜索(BFS, Breadth First Search)是一个针对图和树的遍历算法。发明于上世纪50年代末60年代初，最初用于解决迷宫最短路径和网络路由等问题。
对于下面的树而言，BFS方法首先从根节点1开始，其搜索节点顺序是1,2,3,4,5,6,7,8。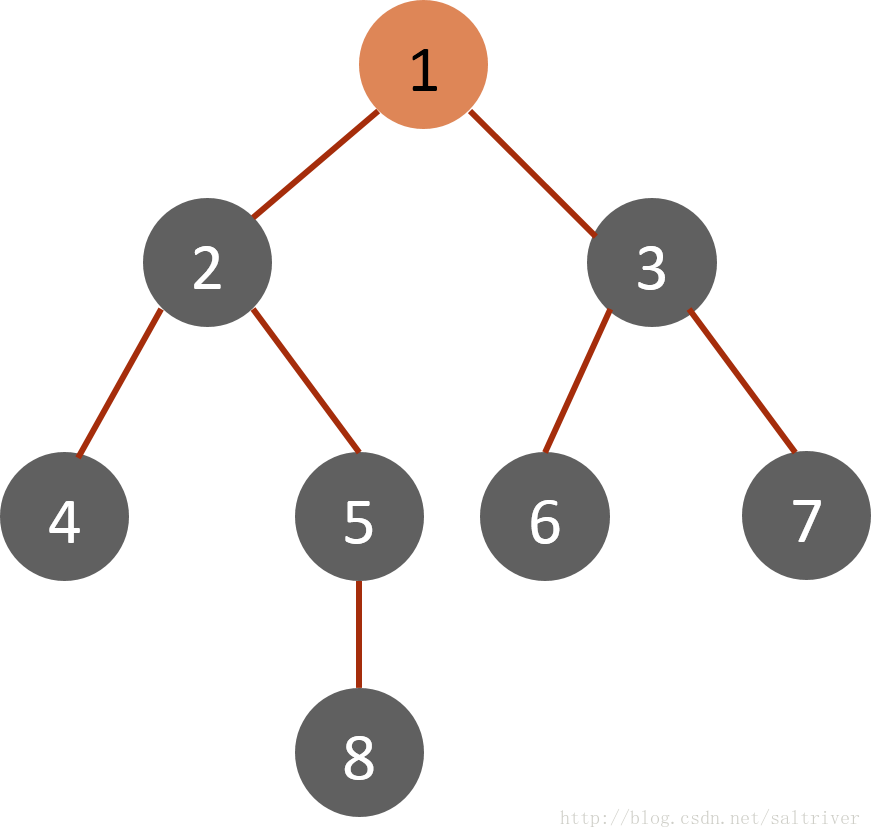

BFS使用队列(queue)来实施算法过程，队列(queue)有着先进先出FIFO(First Input First Output)的特性，
BFS操作步骤如下：
1、把起始点放入queue；
2、重复下述2步骤，直到queue为空为止：
1) 从queue中取出队列头的点；
2) 找出与此点邻接的且尚未遍历的点，进行标记，然后全部放入queue中。
下面结合一个图(graph)的实例，说明BFS的工作过程和原理：
（1）将起始节点1放入队列中，标记为已遍历：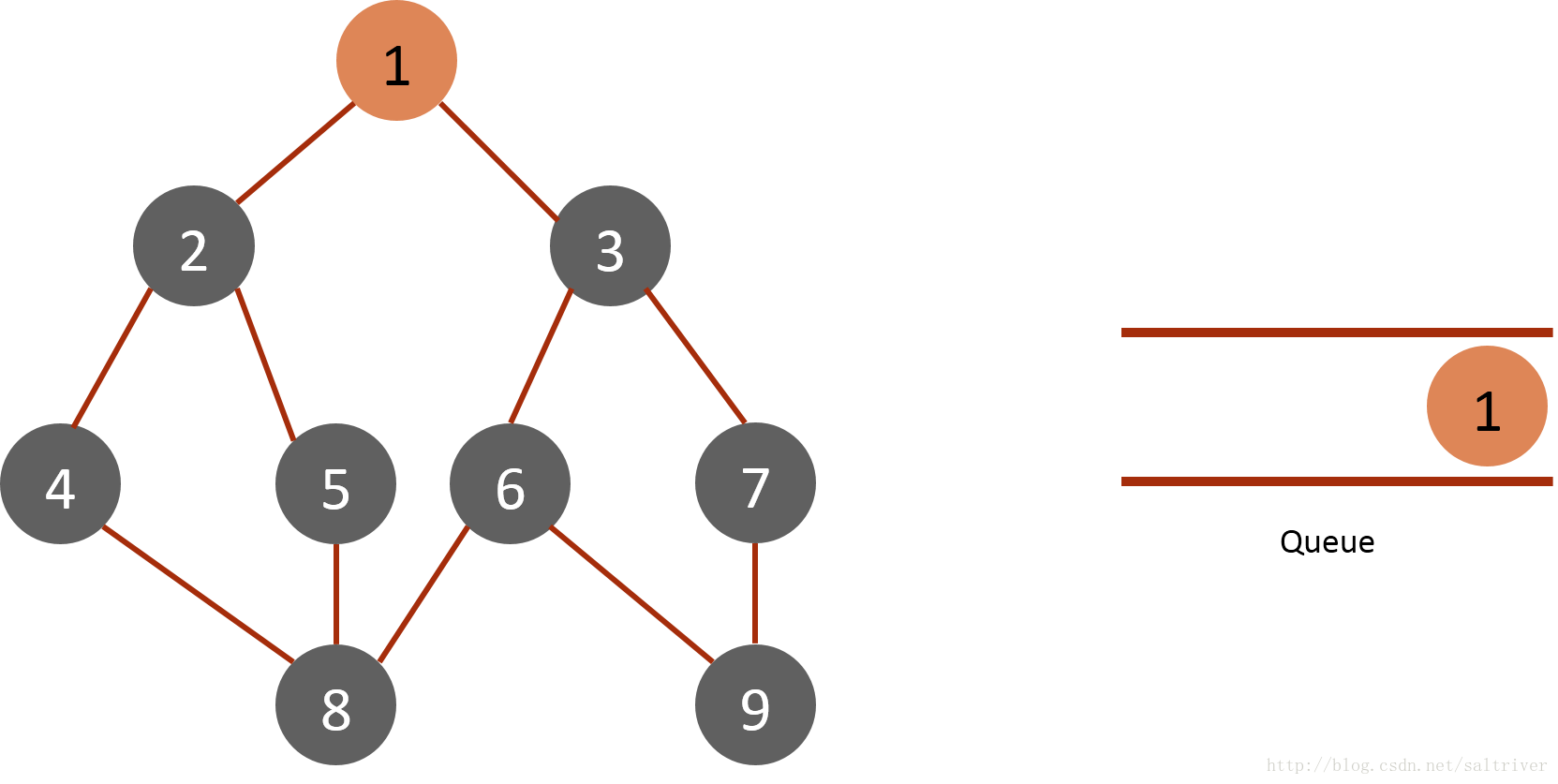

（2）从queue中取出队列头的节点1，找出与节点1邻接的节点2,3，标记为已遍历，然后放入queue中。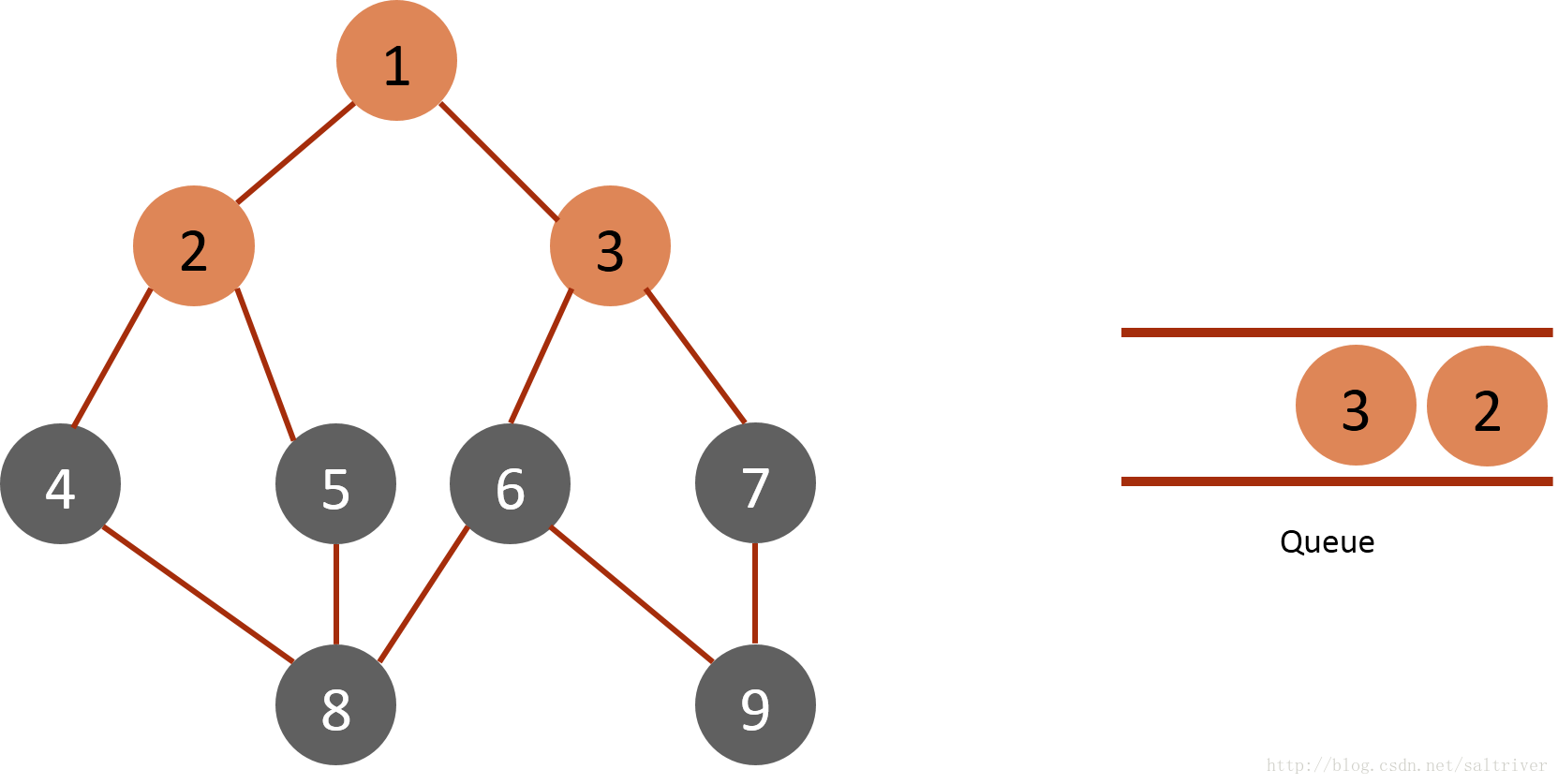

（3）从queue中取出队列头的节点2，找出与节点2邻接的节点1,4,5，由于节点1已遍历，排除；标记4,5为已遍历，然后放入queue中。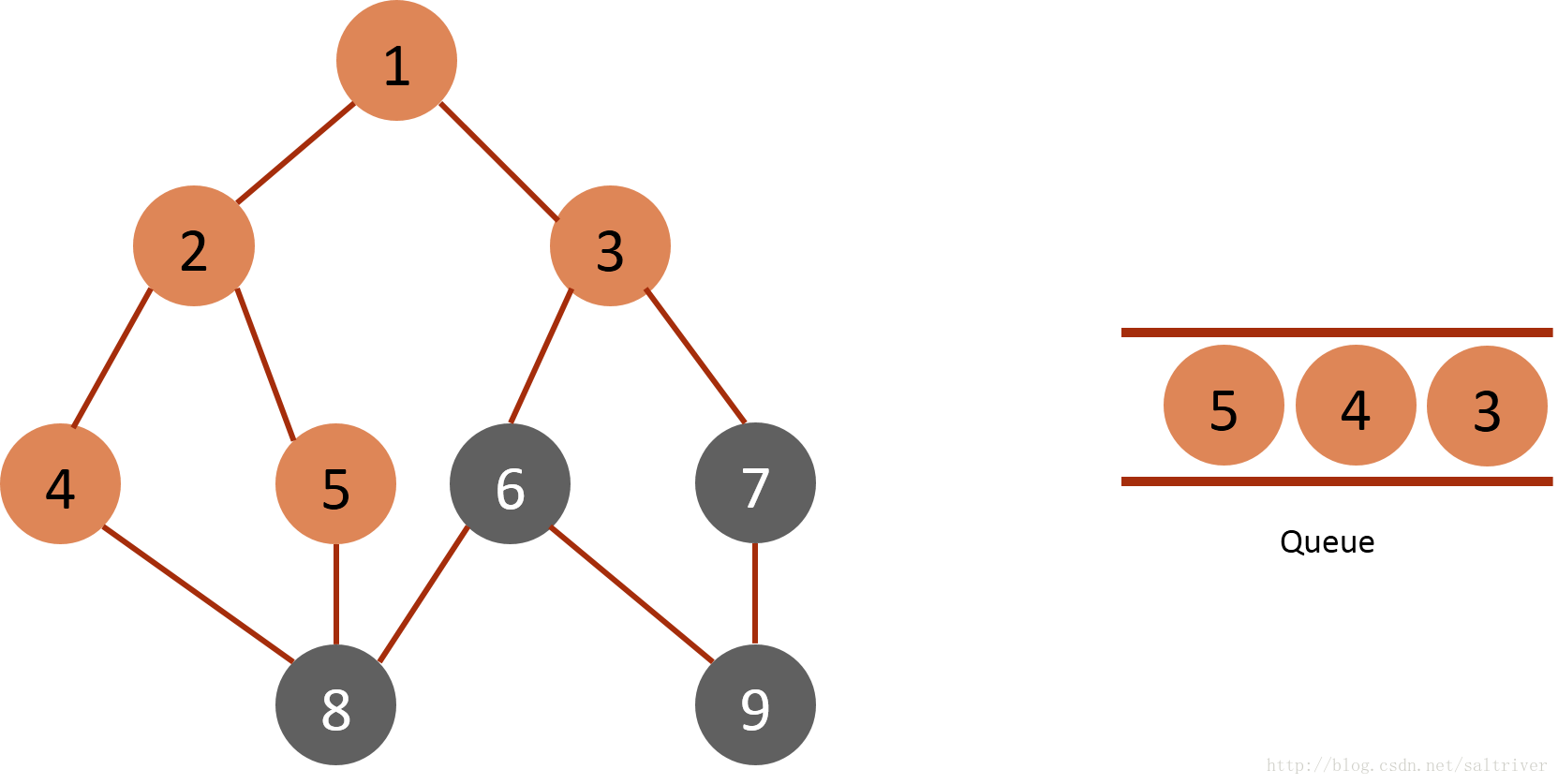

（4）从queue中取出队列头的节点3，找出与节点3邻接的节点1,6,7，由于节点1已遍历，排除；标记6,7为已遍历，然后放入queue中。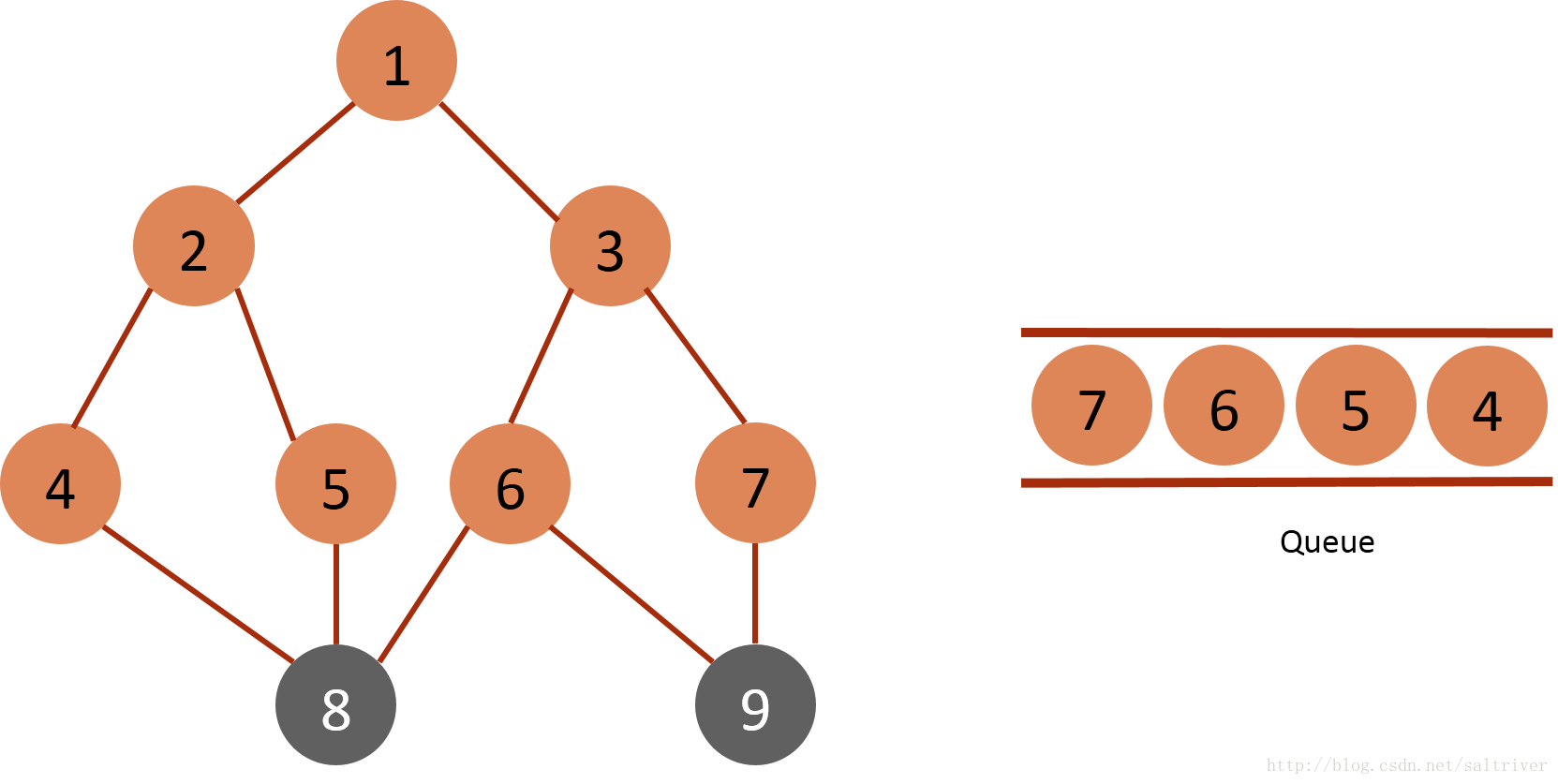

（5）从queue中取出队列头的节点4，找出与节点4邻接的节点2,8，2属于已遍历点，排除；因此标记节点8为已遍历，然后放入queue中。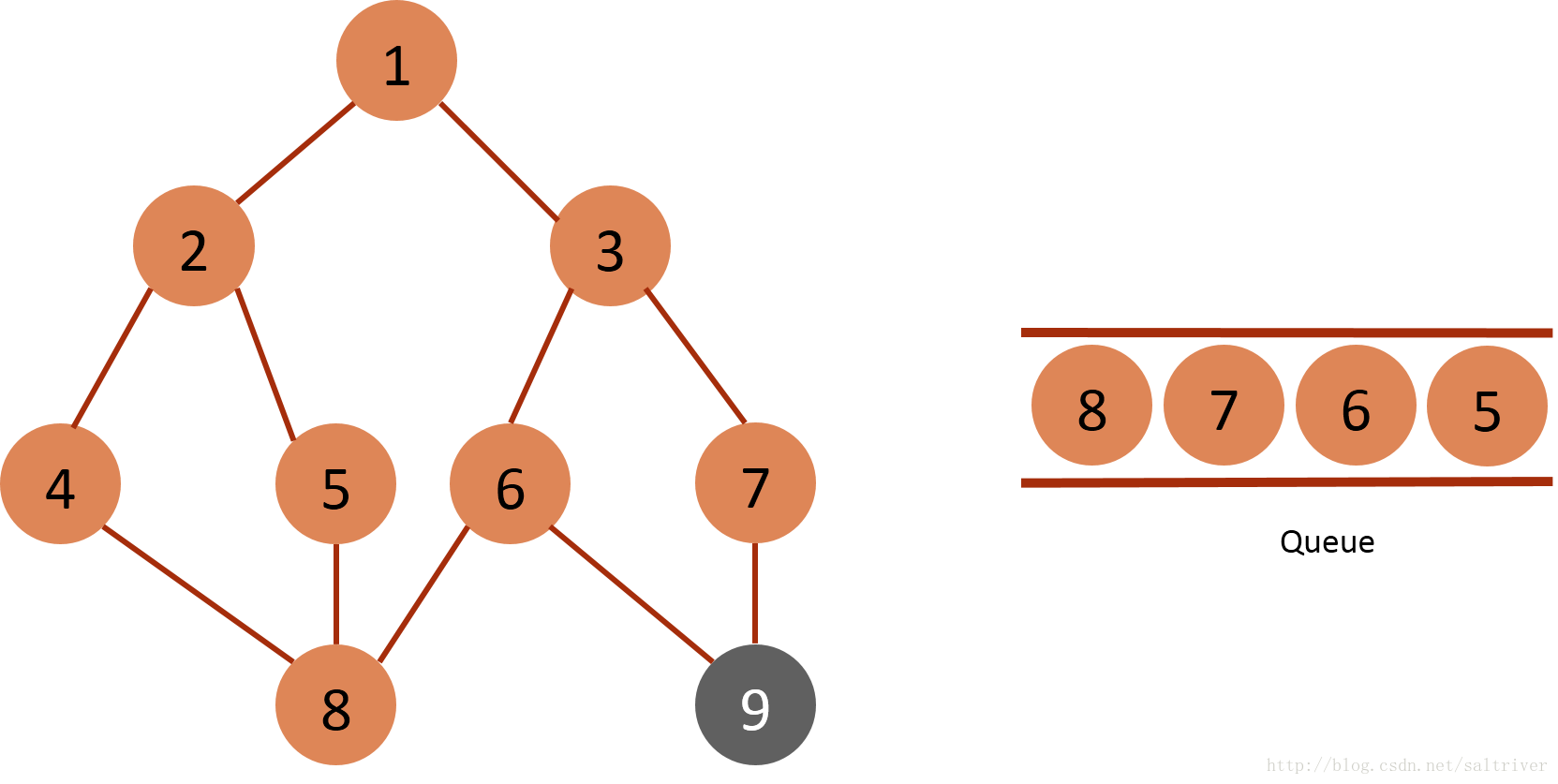

（6）从queue中取出队列头的节点5，找出与节点5邻接的节点2,8，2,8均属于已遍历点，不作下一步操作。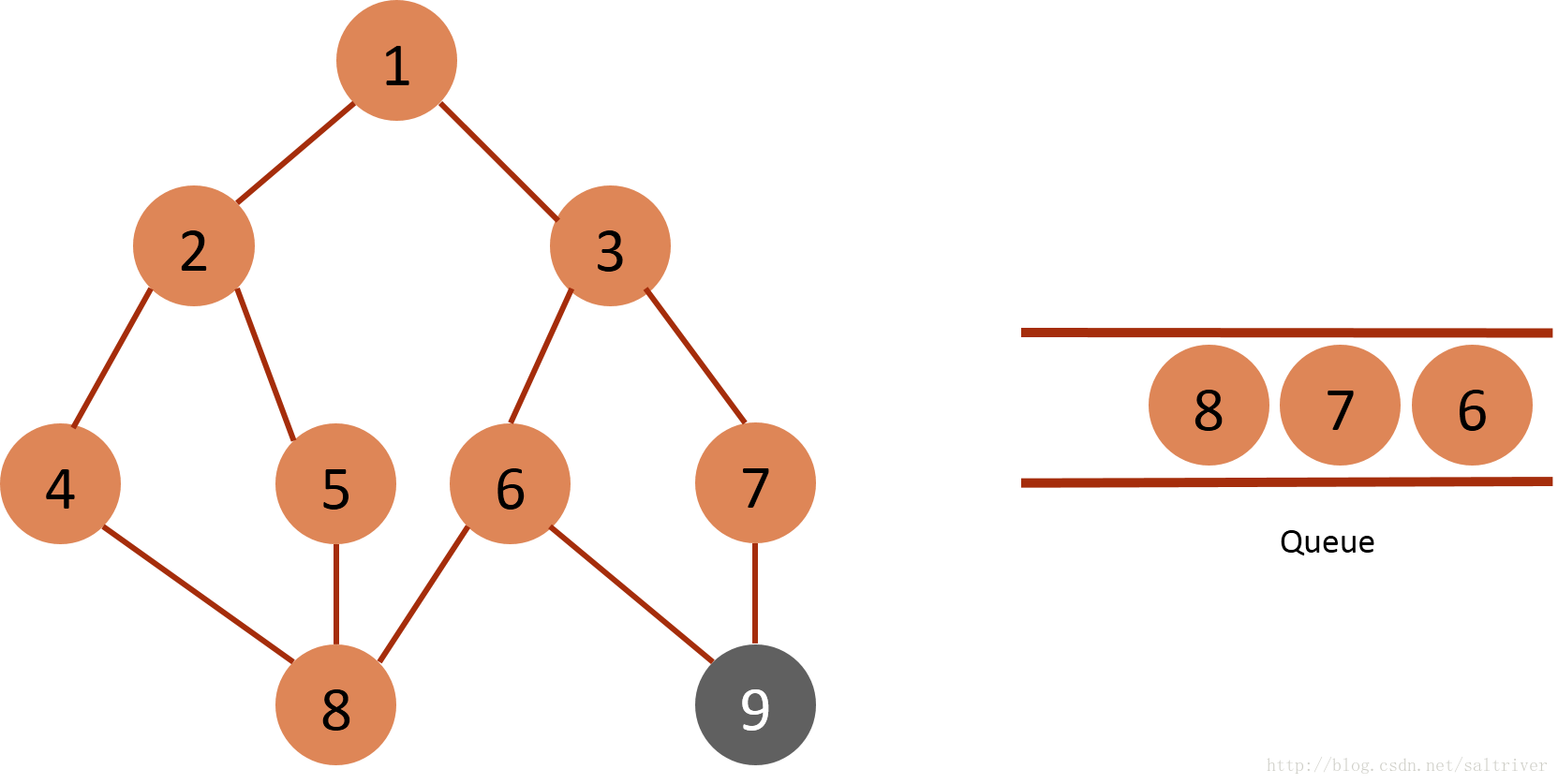

（7）从queue中取出队列头的节点6，找出与节点6邻接的节点3,8,9，3,8属于已遍历点，排除；因此标记节点9为已遍历，然后放入queue中。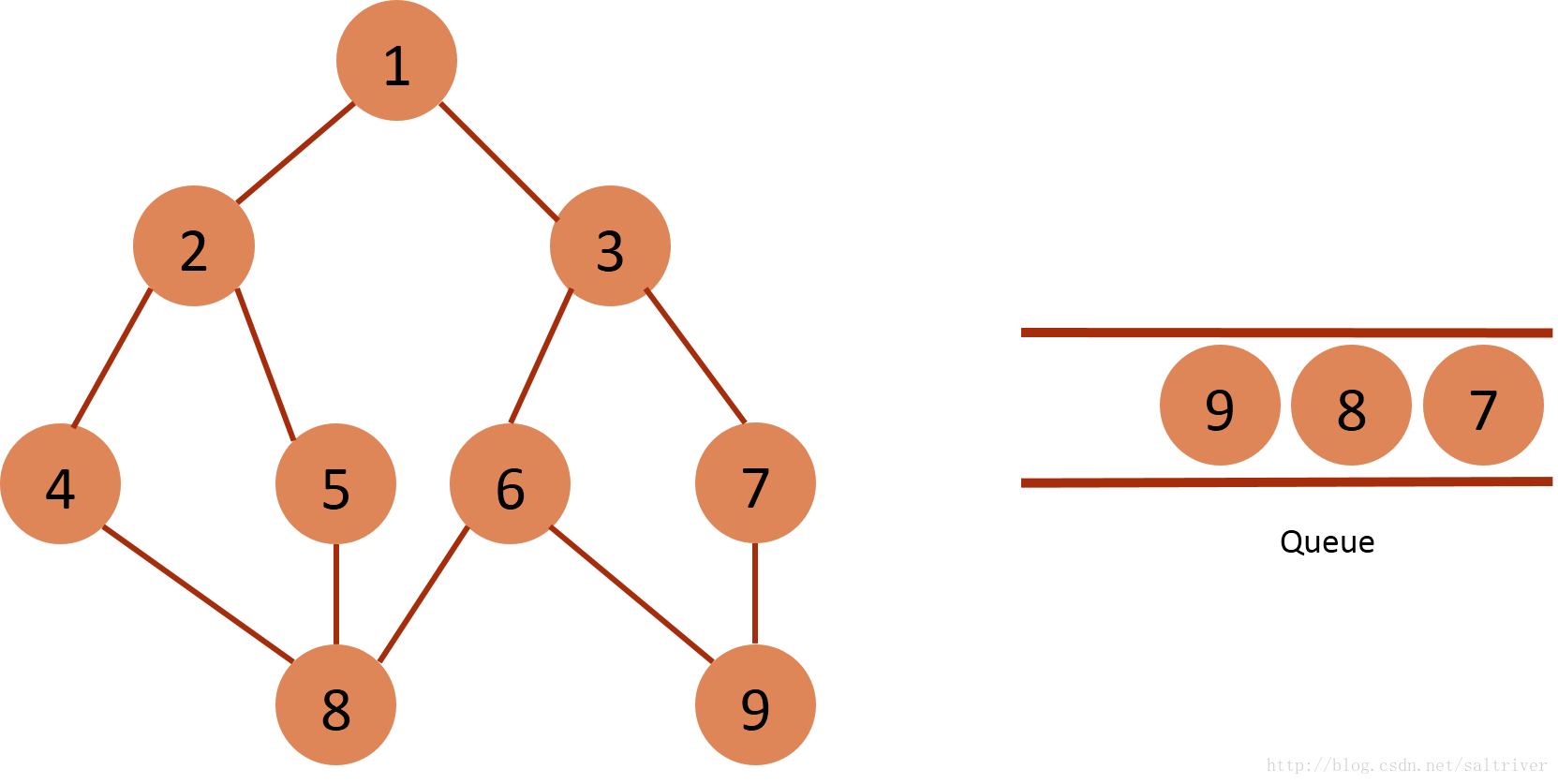

（8）从queue中取出队列头的节点7，找出与节点7邻接的节点3, 9，3,9属于已遍历点，不作下一步操作。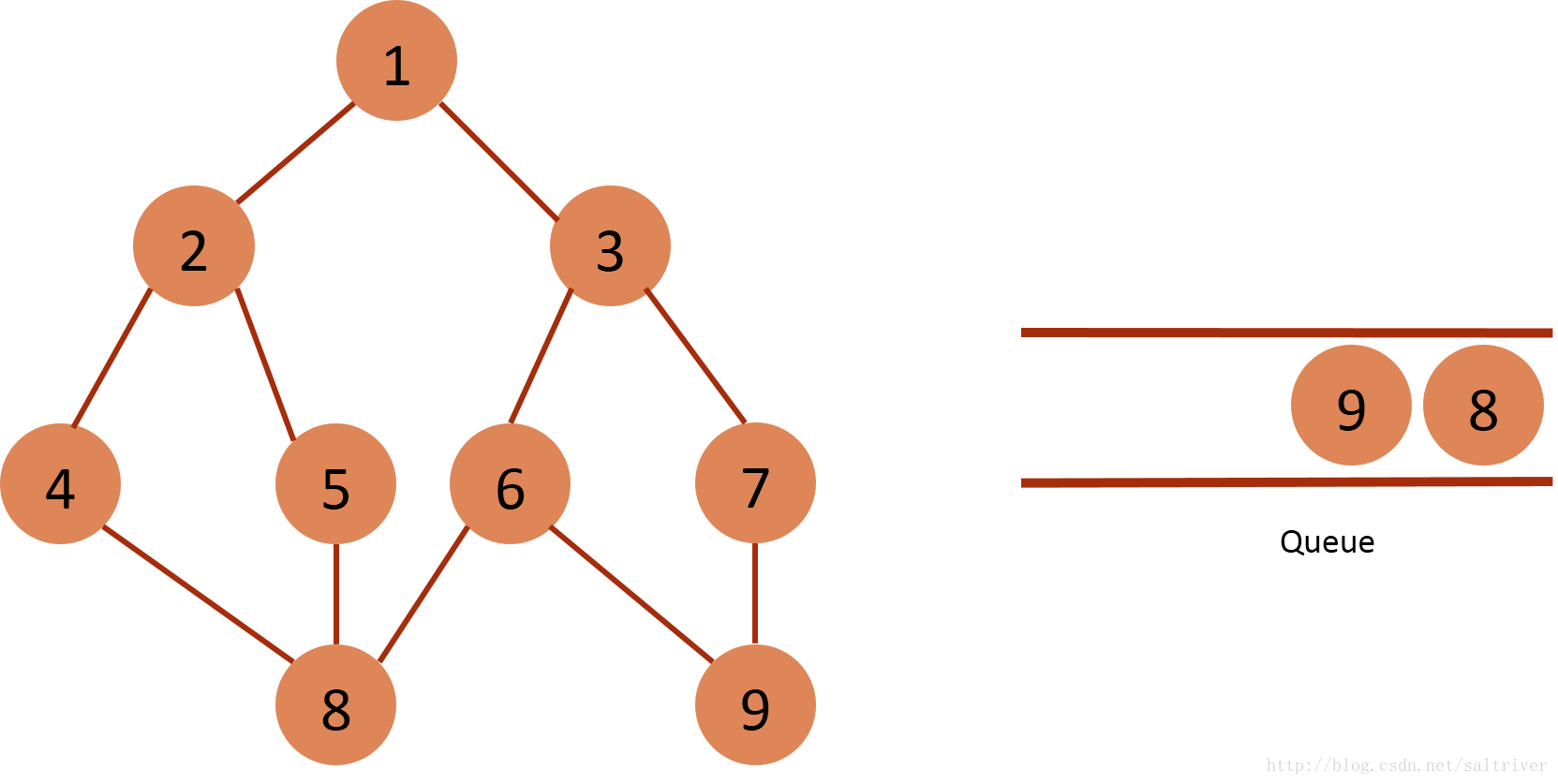

（9）从queue中取出队列头的节点8，找出与节点8邻接的节点4,5,6，4,5,6属于已遍历点，不作下一步操作。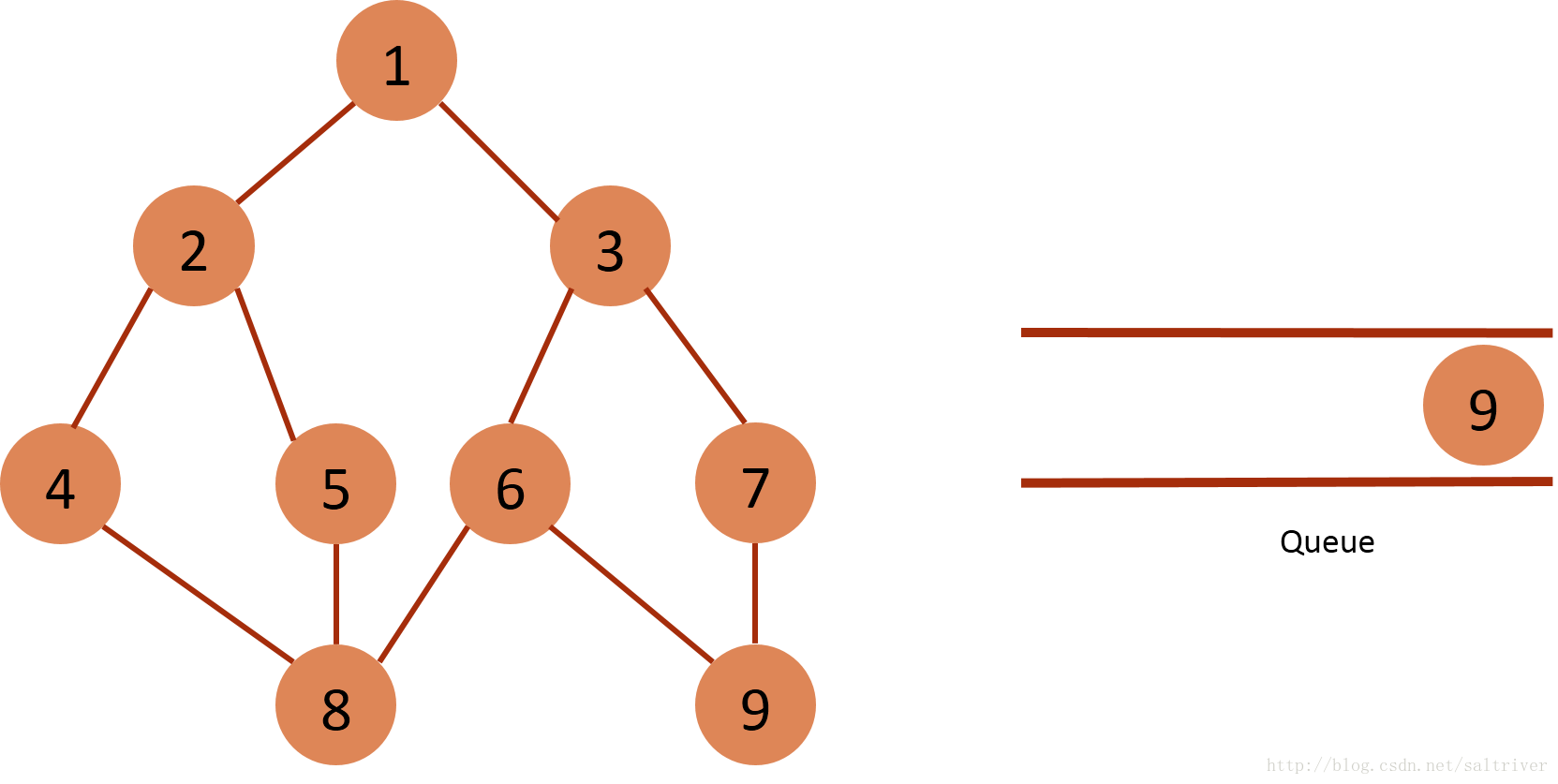

（10）从queue中取出队列头的节点9，找出与节点9邻接的节点6,7，6,7属于已遍历点，不作下一步操作。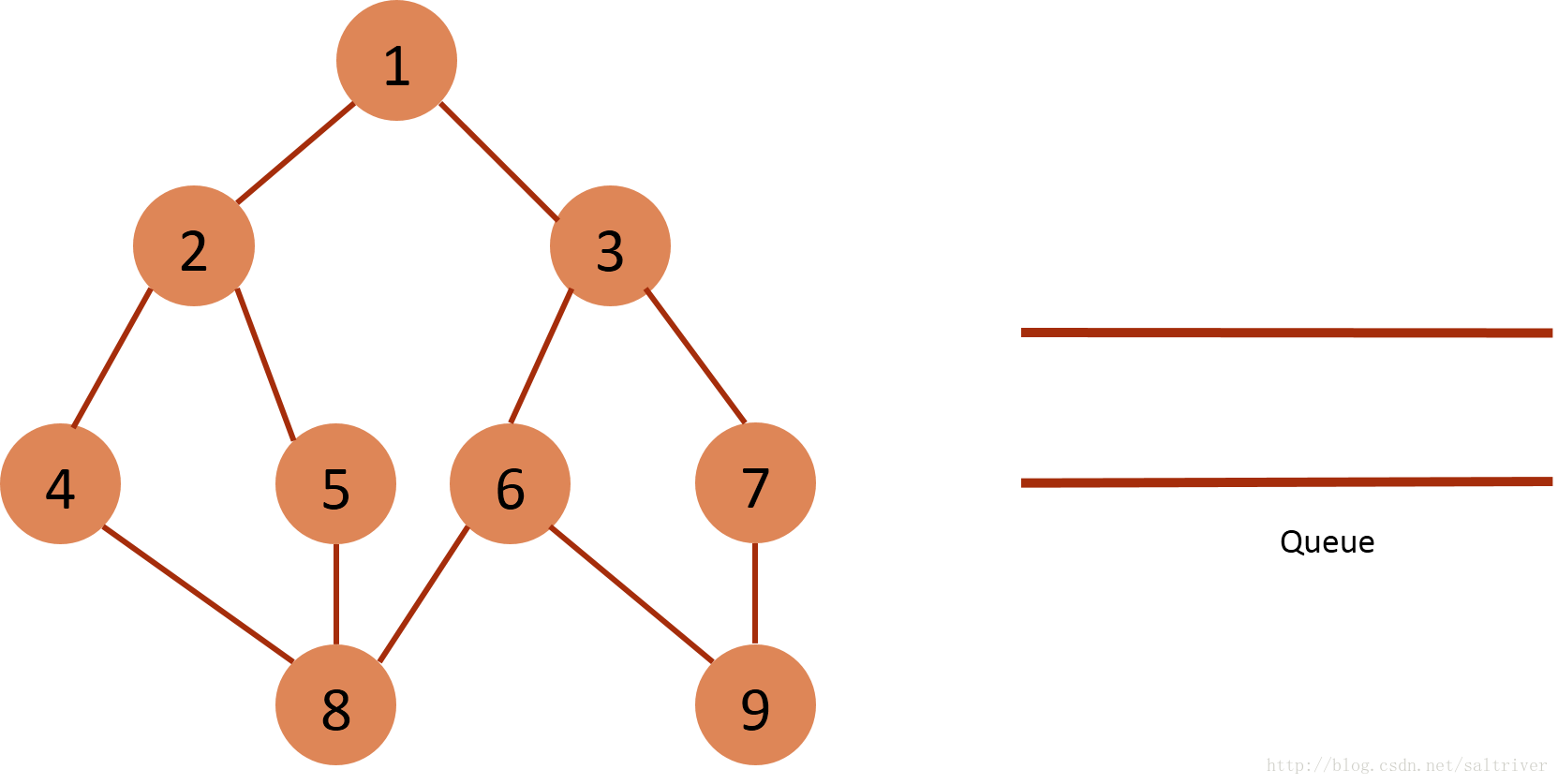

（11）queue为空，BFS遍历结束。

图论（五）深度优先搜索DFS

saltriver 2017-01-14 21:27:17 15114
分类专栏： 数据结构与算法 文章标签： dfs 搜索 遍历
版权
深度优先搜索(DFS, Depth First Search)是一个针对图和树的遍历算法。早在19世纪就被用于解决迷宫问题。
对于下面的树而言，DFS方法首先从根节点1开始，其搜索节点顺序是1,2,3,4,5,6,7,8（假定左分枝和右分枝中优先选择左分枝）。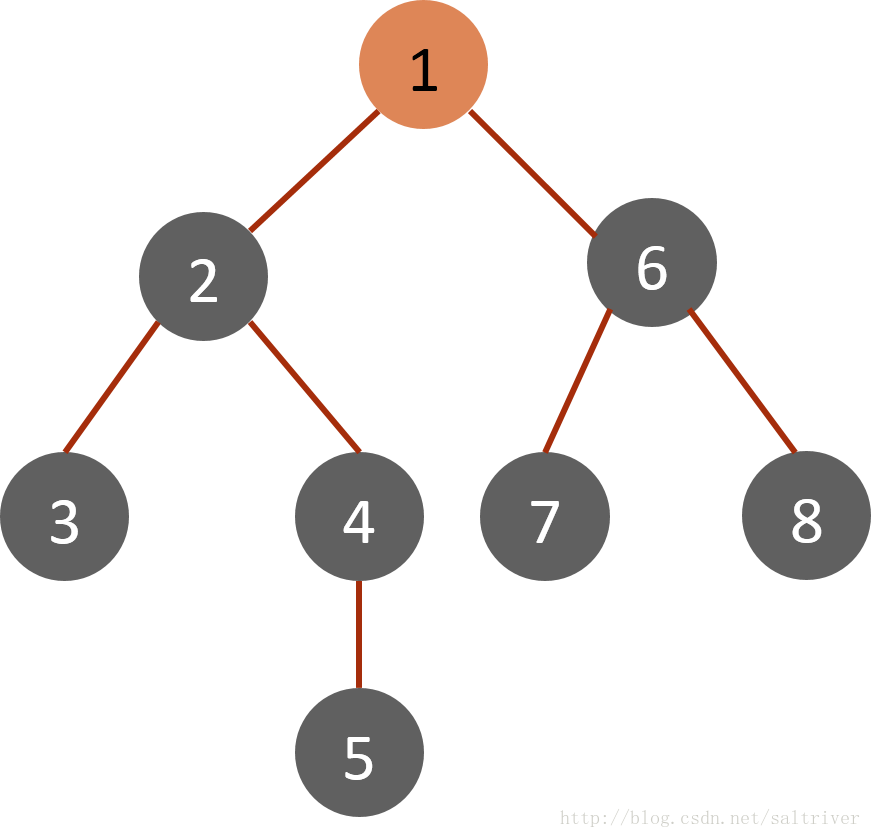

DFS的实现方式相比于BFS应该说大同小异，只是把queue换成了stack而已，stack具有后进先出LIFO(Last Input First Output)的特性，DFS的操作步骤如下：
1、把起始点放入stack；
2、重复下述3步骤，直到stack为空为止：

• 从stack中访问栈顶的点；
• 找出与此点邻接的且尚未遍历的点，进行标记，然后全部放入stack中；
• 如果此点没有尚未遍历的邻接点，则将此点从stack中弹出。

下面结合一个图(graph)的实例，说明DFS的工作过程和原理：
（1）将起始节点1放入栈stack中，标记为已遍历。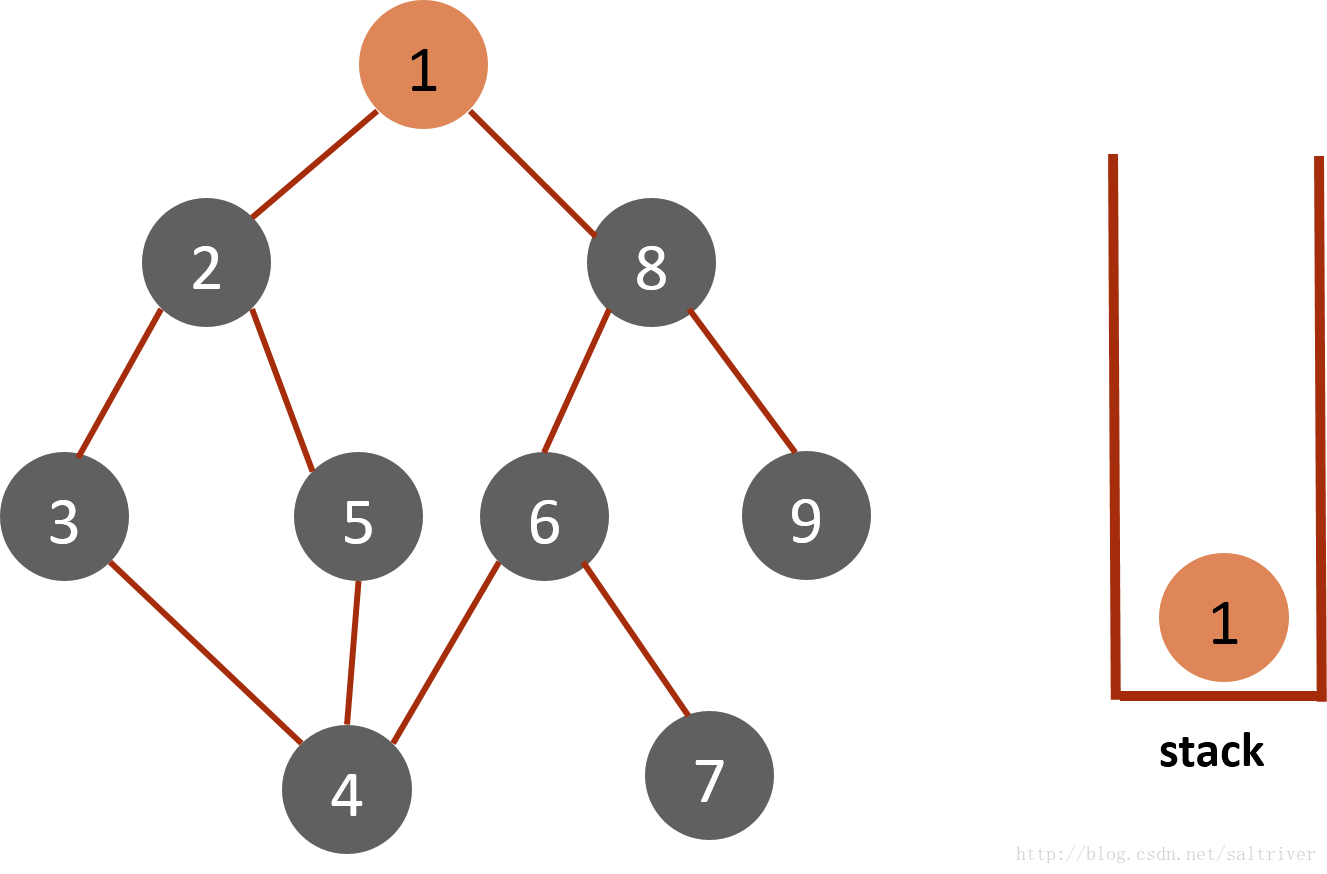

（2）从stack中访问栈顶的节点1，找出与节点1邻接的节点，有2,9两个节点，我们可以选择其中任何一个，选择规则可以人为设定，这里假设按照节点数字顺序由小到大选择，选中的是2，标记为已遍历，然后放入stack中。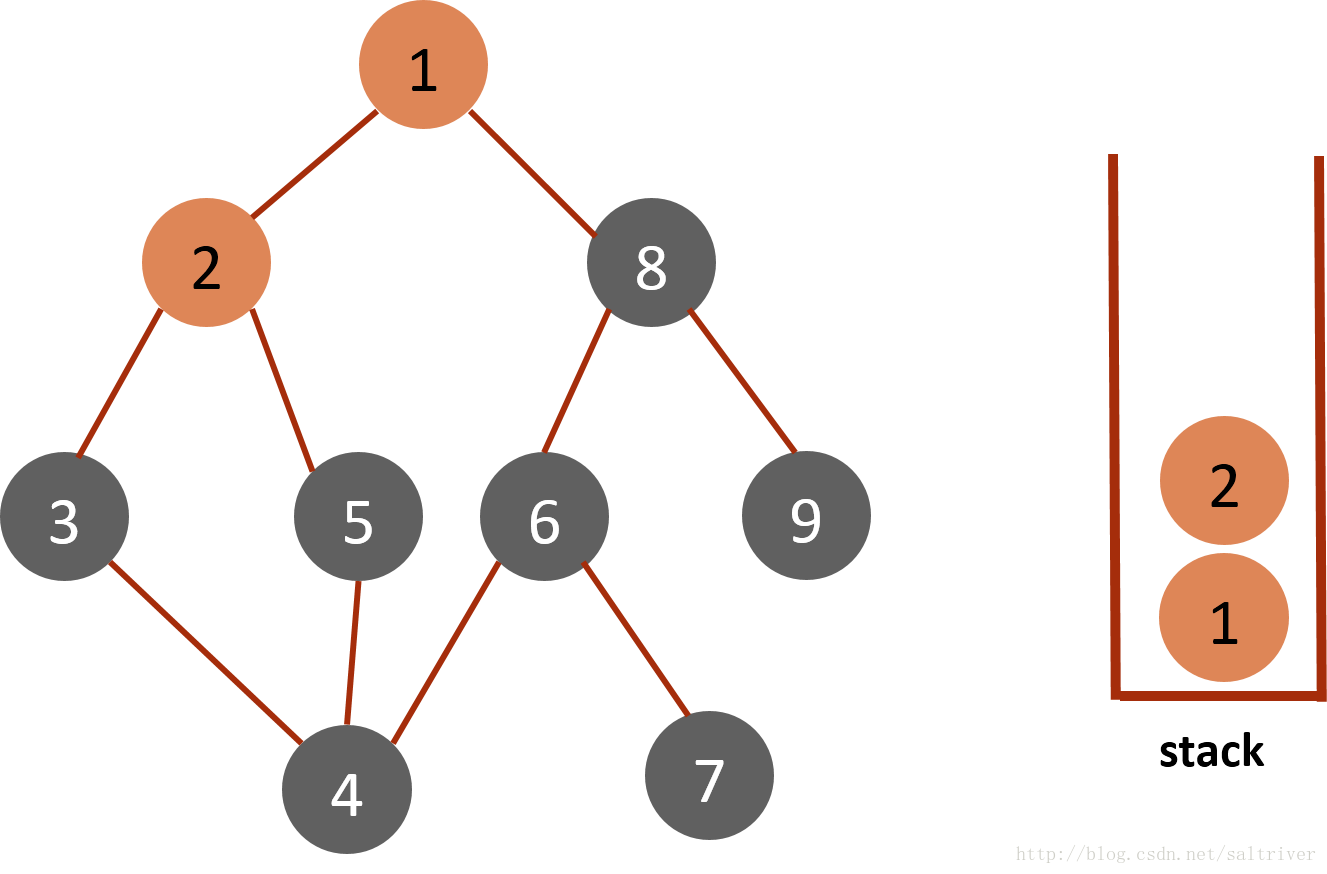

（3）从stack中取出栈顶的节点2，找出与节点2邻接的节点，有1,3,5三个节点，节点1已遍历过，排除；3,5中按照预定的规则选中的是3，标记为已遍历，然后放入stack中。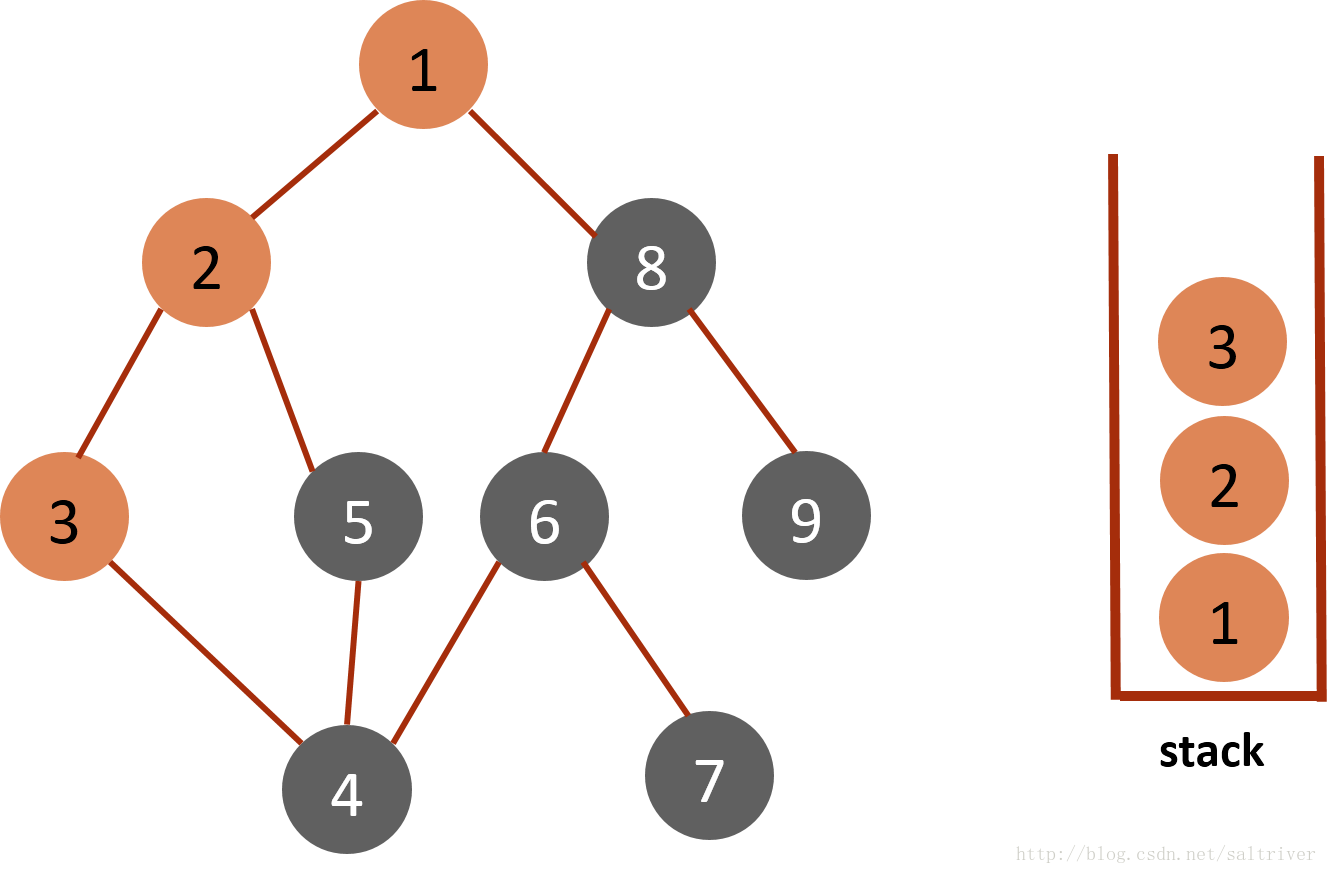

（4）从stack中取出栈顶的节点3，找出与节点3邻接的节点，有2,4两个节点，节点2已遍历过，排除；选中的是节点4，标记为已遍历，然后放入stack中。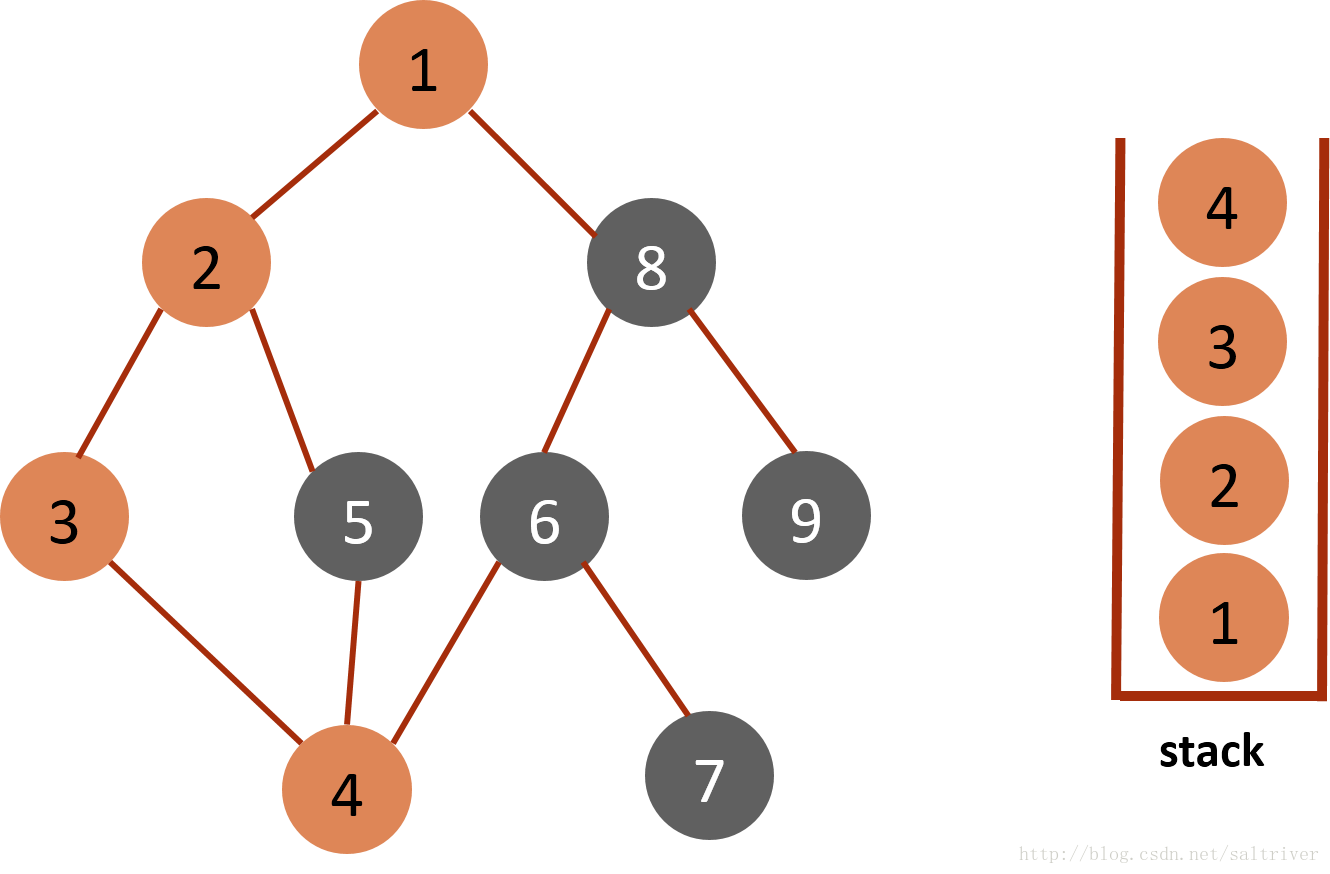

（5）从stack中取出栈顶的节点4，找出与节点4邻接的节点，有3,5,6三个节点，节点3已遍历过，排除；选中的是节点5，标记为已遍历，然后放入stack中。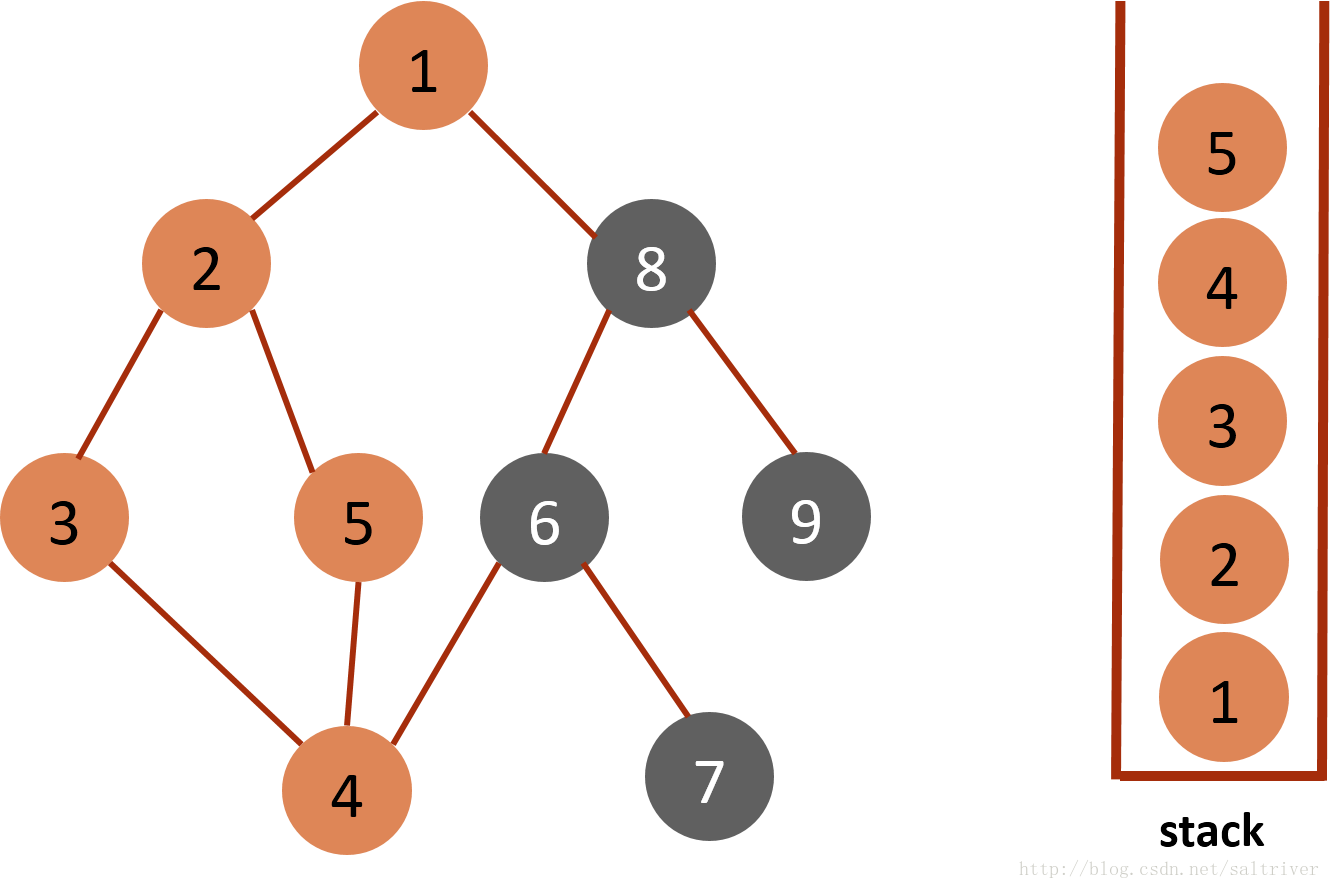

（6）从stack中取出栈顶的节点5，找出与节点5邻接的节点，有2,4两个节点，节点2,4都已遍历过，因此节点5没有尚未遍历的邻接点，则将此点从stack中弹出。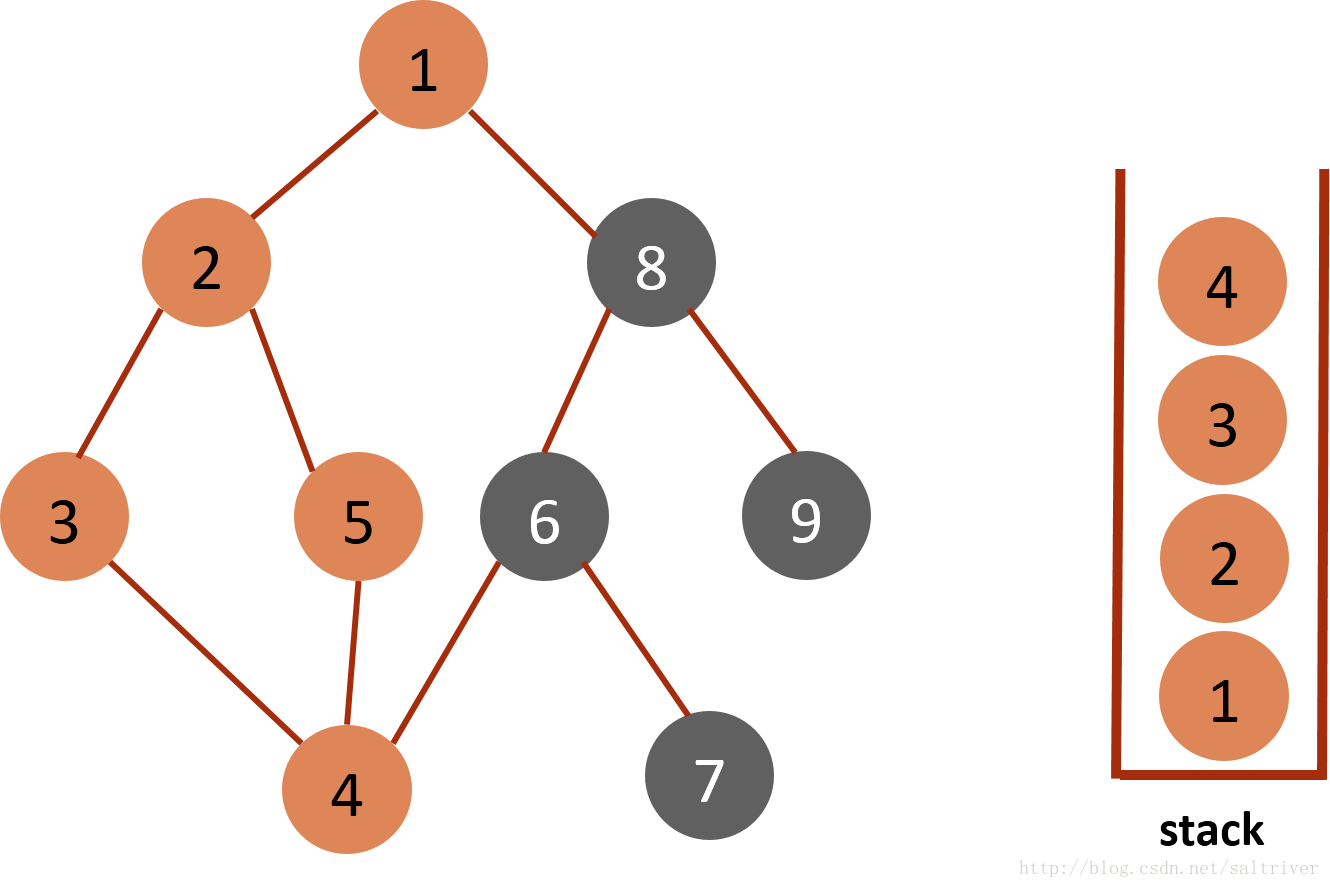

（7）当前stack栈顶的节点是4，找出与节点4邻接的节点，有3,5,6三个节点，节点3,5都已遍历过，排除；选中的是节点6，标记为已遍历，然后放入stack中。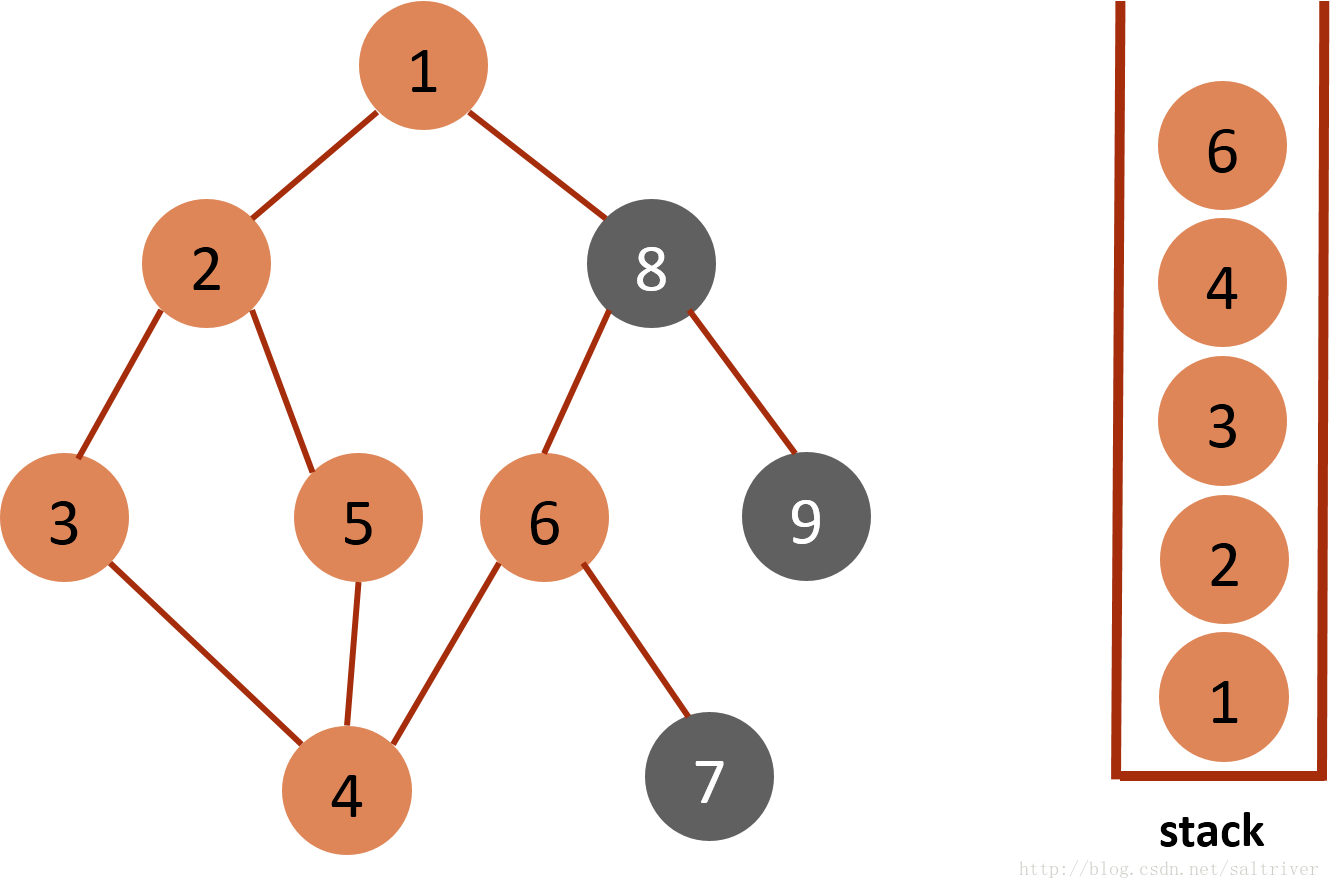

（8）当前stack栈顶的节点是6，找出与节点6邻接的节点，有4,7,8三个节点，4已遍历，按照规则选中的是7，标记为已遍历，然后放入stack中。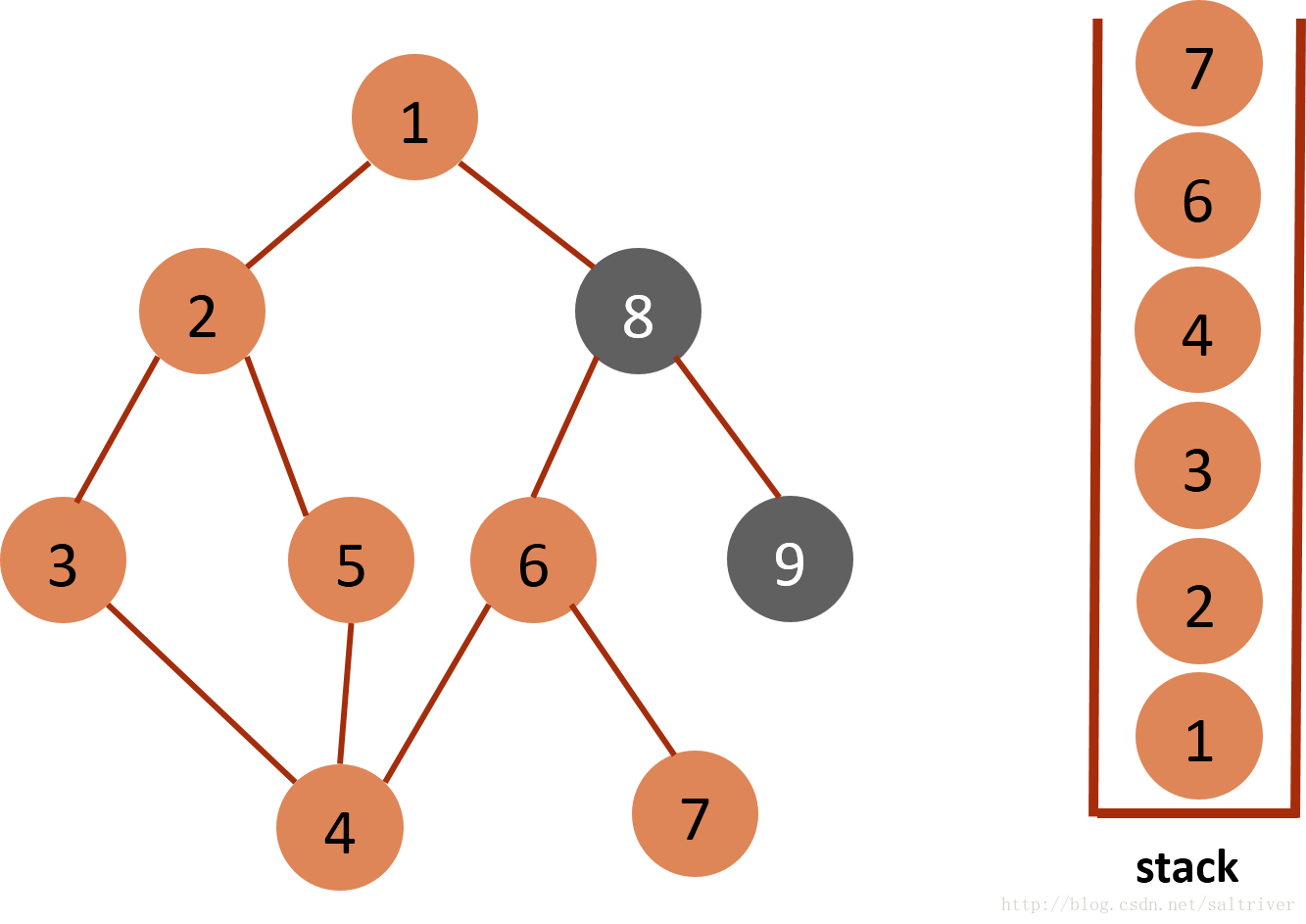

（9）当前stack栈顶的节点是7，找出与节点7邻接的节点，只有节点6，已遍历过，因此没有尚未遍历的邻接点，将节点7从stack中弹出。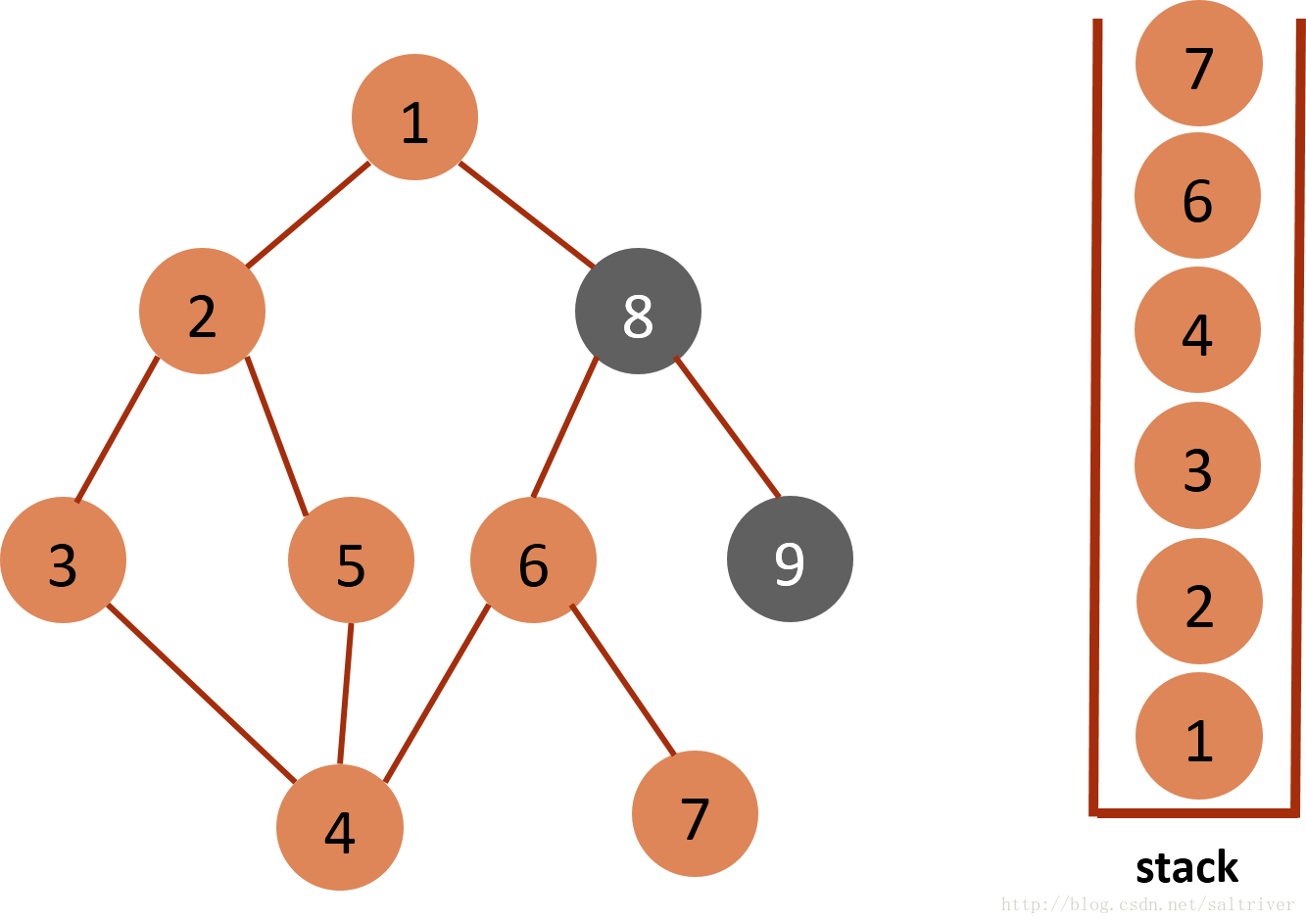

（10）当前stack栈顶的节点是6，找出与节点6邻接的节点，有节点7,8，7已遍历过，因此将节点8放入stack中。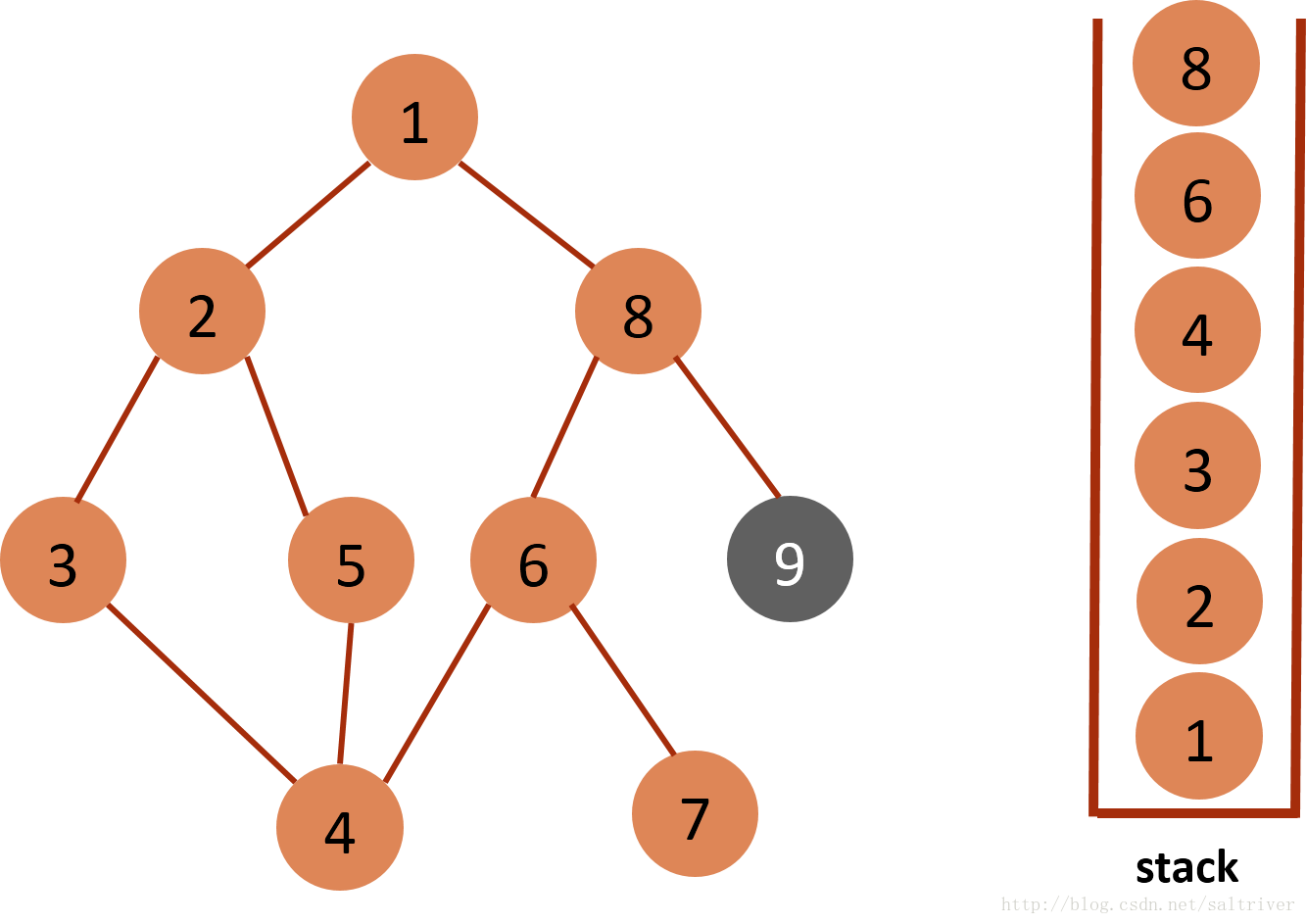

（11）当前stack栈顶的节点是8，找出与节点8邻接的节点，有节点1,6,9，1,6已遍历过，因此将节点9放入stack中。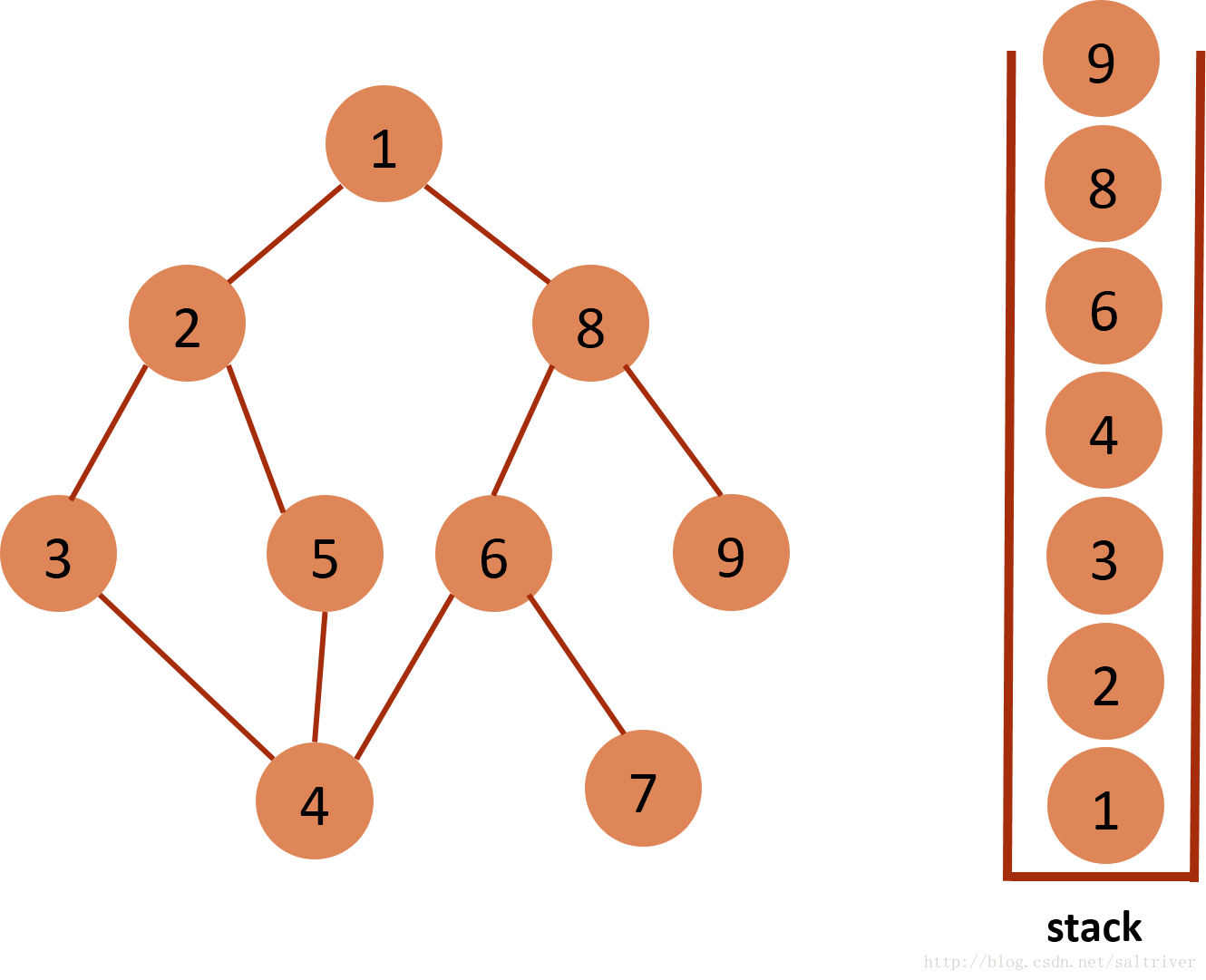

（12）当前stack栈顶的节点是9，没有尚未遍历的邻接点，将节点9弹出，依次类推，栈中剩余节点8,6,4,3,2,1都没有尚未遍历的邻接点，都将弹出，最后栈为空。
（13）DFS遍历完成。