题目FindKthMin

在一个无序数组中怎么找到第k小的数， k从1开始，问怎么O(N)拿下

笔试用的方法

大根堆

// 利用大根堆，时间复杂度O(N*logK)
 public static int minKth(int[] arr, int k) {
     PriorityQueue<Integer> maxHeap = new PriorityQueue<>((o1, o2) -> {
         return o2 - o1;
     });
     for (int i = 0; i < k; i++) {
         maxHeap.add(arr[i]);
     }
     for (int i = k; i < arr.length; i++) {
         if (arr[i] < maxHeap.peek()) {
             maxHeap.poll();
             maxHeap.offer(arr[i]);
         }
     }
     return maxHeap.peek();
 }

借鉴快排思路

借用快排的思路，但又不是快排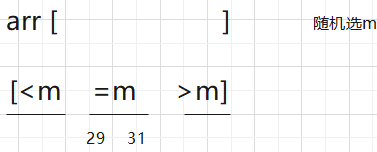

快排的做法是，随机选一个数m，不动，然后左边去递归，右边去递归，
而这里我们是只会进左右两侧的某一侧的，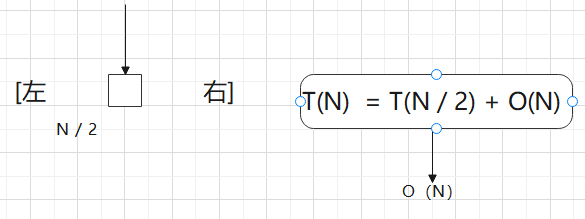

 // 改写快排，时间复杂度O(N)
public static int minKth2(int[] arr, int k) {
    return process2(arr, 0, arr.length - 1, k - 1);
}
// arr 第k小的数
// process2(arr, 0, N-1, k-1)
// arr[L..R]  范围上，如果排序的话(不是真的去排序)，找位于index的数
// index [L..R]
public static int process2(int[] arr, int L, int R, int index) {
    if (L == R) {
        return arr[L];
    }
    int pivot = arr[L + (int) (Math.random() * (R - L + 1))];
    int[] range = partition(arr, L, R, pivot);
    if (index >= range[0] && index <= range[1]) {
        return arr[index];
    } else if (index < range[0]) {
        return process2(arr, L, range[0] - 1, index);
    } else {
        return process2(arr, range[1] + 1, R, index);
    }
}
private static int[] partition(int[] arr, int L, int R, int pivot) {
    int less = L - 1;
    int more = R + 1;
    int cur = L;
    while (cur < more) {
        if (arr[cur] < pivot) {
            swap(arr, ++less, cur++);
        } else if (arr[cur] > pivot) {
            swap(arr, cur, --more);
        } else {
            cur++;
        }
    }
    return new int[]{less + 1, more - 1};
}
private static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

bfprt算法（跟面试官吹牛逼用的）

不需要像快排那样的概率累加，我也能让你收敛到O(n), 我是用严格的流程

我们刚刚上面讲的算法流程是这样的， bfprt算法与它后面的流程全都一样，只是第一步怎么选一个数不一样

那么它是如何选出这个数m的呢？

1）逻辑上每5个数分为一组，共有N / 5组
2）每个组内部单独排序一下，但组与组之间仍然是无序的，
3）取出每个组的中位数，如果最后一个组不足5个，那就取上中位数或者下中位数，不要两个相加/2,
这些数组成数组m[ ]
4) 找出数组m[ ]的中位数，递归调用bfprt（m， N / 10）
———> 这个结果就是我们要的数m了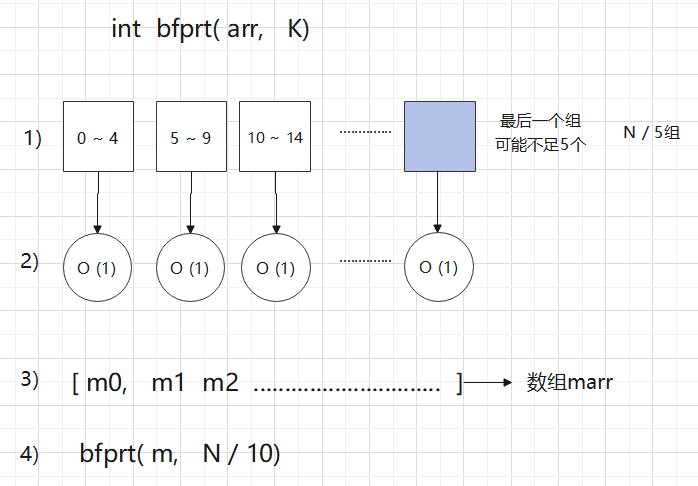

看一下时间复杂度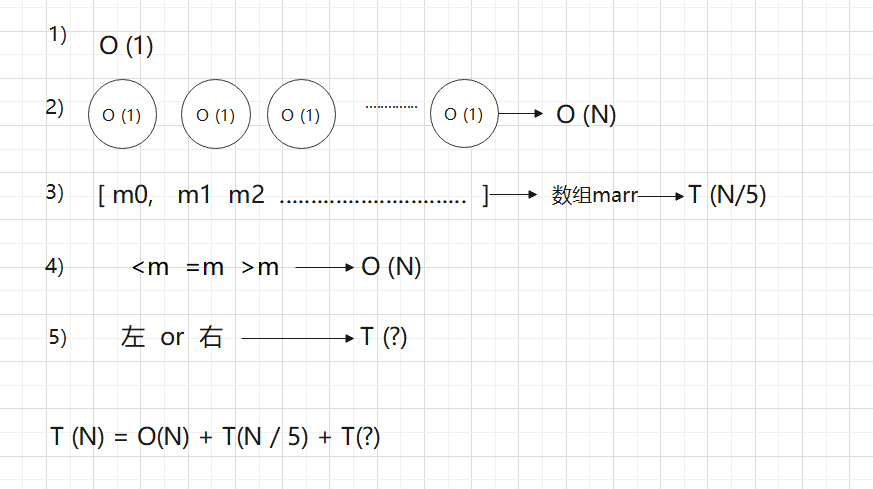

现在就是确定一下T（？）也就是第5步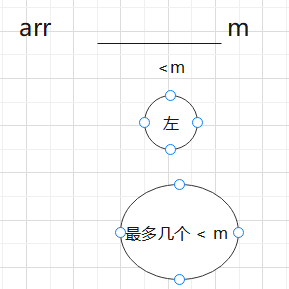

如果我进m左侧的递归时，我如果可以在arr中直到最多有几个< m, 那么我就知道我递归的规模有多大了。
所以我们可以这样反推 N - 大于等于m的至少有几个数 = 最多有几个 < m

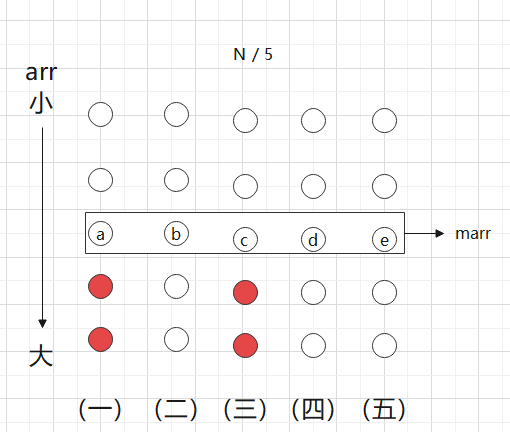
m数组就是[a, b, c, d, e]
要选出这个数组中的第三小，假设是e，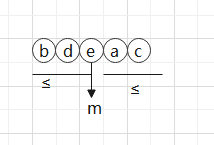

有N / 10个数比e大，对应回原来的数组中，比a大的还有2个，比c大的也有2个，
所以总共有 N / 10 * 3 = 十分之三N 的规模比e大，那么就有十分之七N规模比e小，那么左侧递归的规模不就知道了么

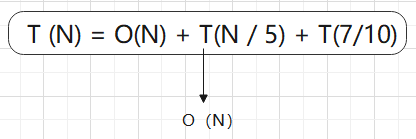
所以全部时间复杂度就求出来了 O(N)

// arr[L..R]  如果排序的话，位于index位置的数，是什么，返回
private static int bfprt(int[] arr, int L, int R, int index) {
    if (L == R) {
        return arr[L];
    }
    int pivot = medianOfMedians(arr, L, R);
    int[] range = partition(arr, L, R, pivot);
    if (index >= range[0] && index <= range[1]) {
        return arr[index];
    } else if (index < range[0]) {
        return bfprt(arr, L, range[0] - 1, index);
    } else {
        return bfprt(arr, range[1] + 1, R, index);
    }
}
// arr[L...R]  五个数一组
// 每个小组内部排序
// 每个小组中位数领出来，组成marr
// marr中的中位数，返回
private static int medianOfMedians(int[] arr, int L, int R) {
    int size = R - L + 1;
    int offset = size % 5 == 0 ? 0 : 1;
    int[] mArr = new int[size / 5 + offset];
    for (int team = 0; team < mArr.length; team++) {
        int teamFirst = L + team * 5;
        // L ... L + 4
        // L +5 ... L +9
        // L +10....L+14
        mArr[team] = getMedian(arr, teamFirst, Math.min(R, teamFirst + 4));
    }
    // marr中，找到中位数
    // marr(0, marr.len - 1,  mArr.length / 2 )
    return bfprt(mArr, 0, mArr.length - 1, mArr.length / 2);
}
private static int getMedian(int[] arr, int L, int R) {
    insertionSort(arr, L, R);
    return arr[(L + R) / 2];
}
private static void insertionSort(int[] arr, int L , int R) {
    for (int begin = L + 1; begin <= R; begin++) {
        int cur = L;
        while (cur > 0 && arr[cur] < arr[cur - 1]) {
            int tmp = arr[cur];
            arr[cur] = arr[cur - 1];
            arr[cur - 1] = tmp;
            cur--;
        }
    }
}