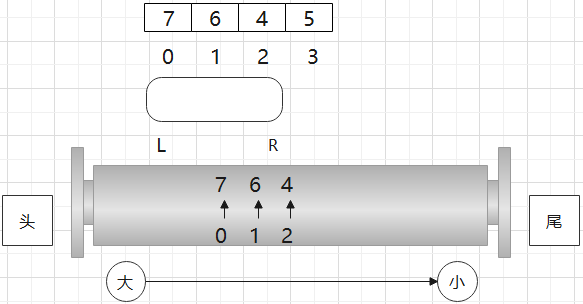
滑动窗口

image.png

  • 保证任何时候L ≤ R

    窗口内的更新结构

  • 维持窗口在滑动时的状态，以便当我们需要这些状态的时候获取的代价比较低

    使用双端队列 java中LinkedList就是双端队列 队列中放的是下标

比如我要的是最大值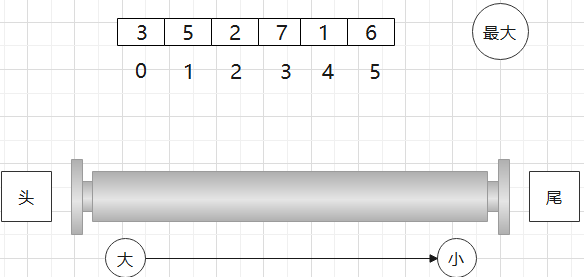
image.png
0位置的3从双端队列尾部进来
image.png
接下来1位置的5要进窗口，从尾部进队列，但是进不来，
要先把在队列中小于它的数从尾部弹出之后，直到它能进去。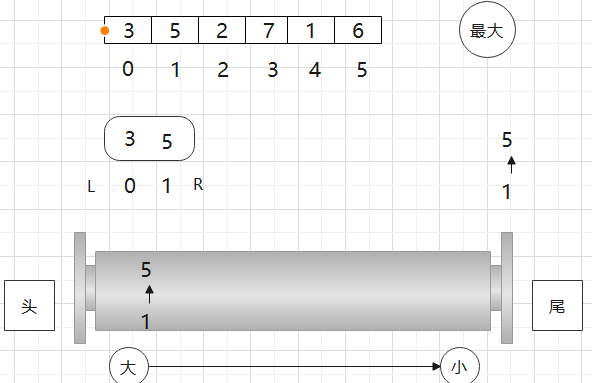
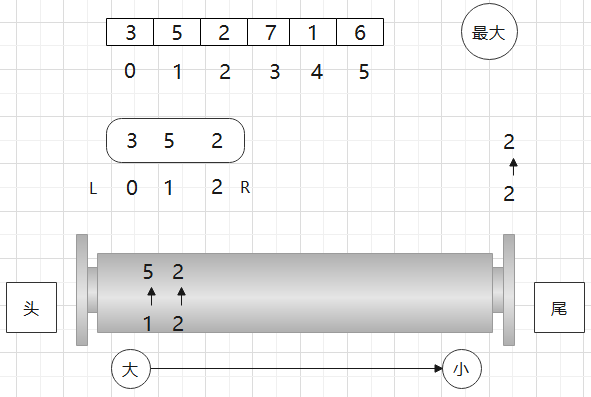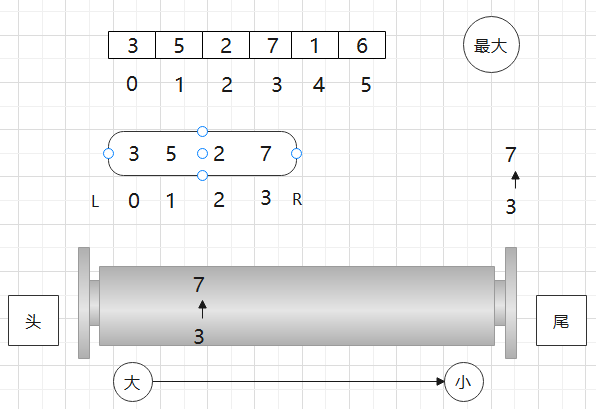
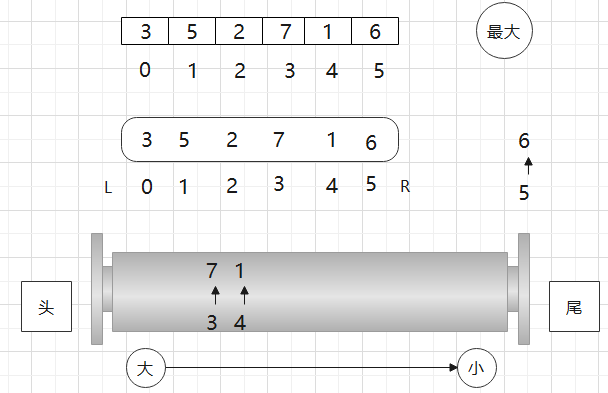
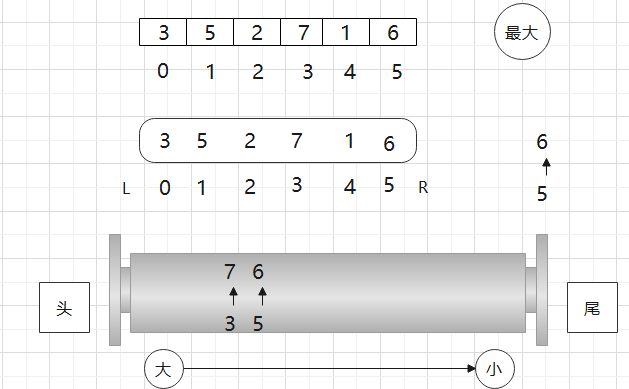
image.png
image.png、
image.png
image.png
image.png

当窗口要缩的时候，这个结构怎么更新？

看这个例子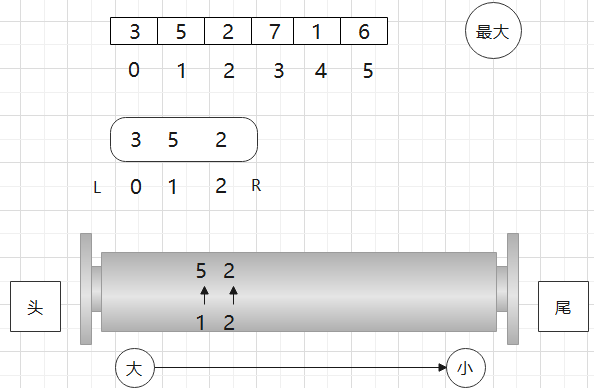
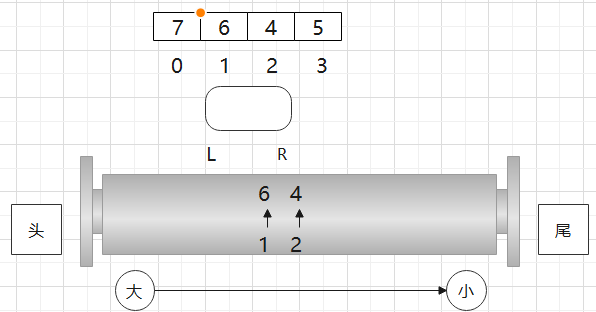
image.png
比如现在L要往右动， 0位置不包含在窗口里了，那么我就看双端队列头部的数是不是0位置的，也就是看一下头部是不是我过期的位置，若不是，则啥都不用干，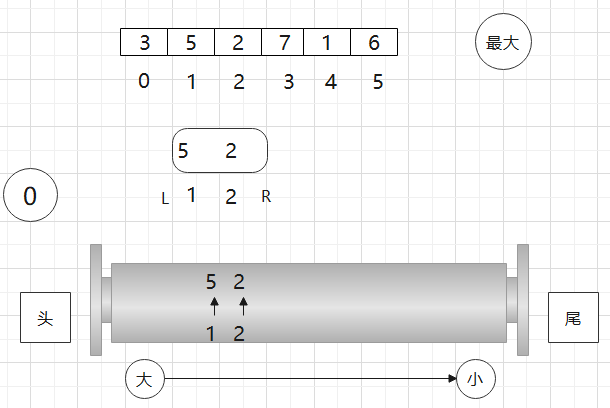
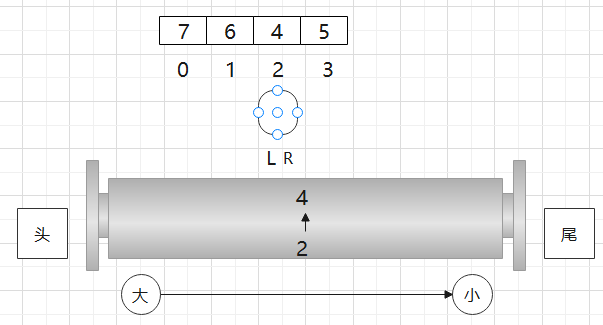
image.png
现在L又往右动，那么1位置就过期了，看一下双端队列头部是不是过期的位置，若是，让它从双端队列头部弹出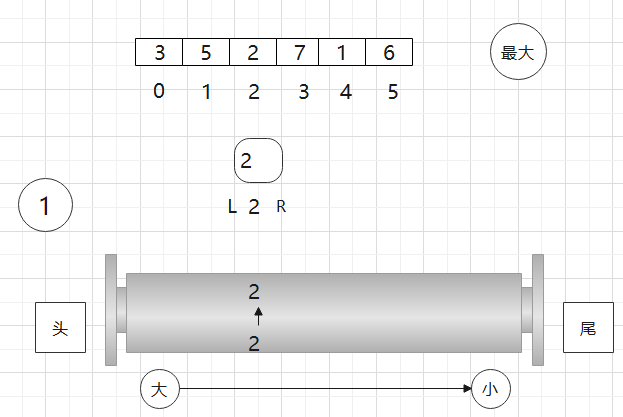
image.png

双端队列头部就是任意时刻下窗口内的最大值

那么这是为啥呢？

  • 比如某一时刻窗口内已经有了一个状况，并且不让R往右动了， 只让L往右动，双端队列的数表明谁依次成为最大值的优先级
    • image.png
    • image.png
    • image.png
  • 回到初始状态，假设现在3位置的5要进来，双端队列为什么可以让2位置的4弹出并舍弃？因为3位置的5值比它大，下标比它晚过期， 永远不会再轮到2位置的4的可能性了

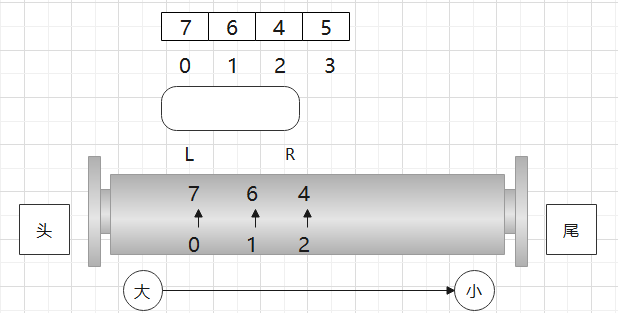
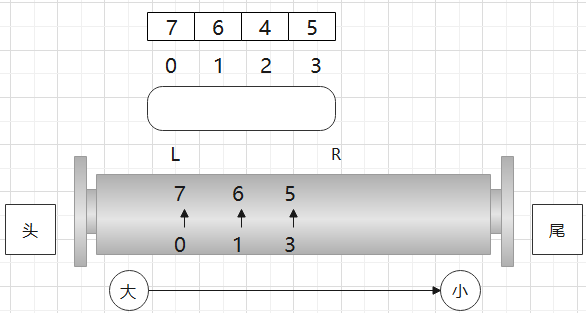
image.png
image.png

  1.   - 现在4位置的8要进来，那么就全扔（我值比你大，下标比你晚过期，轮不着你了）
  2.      - （值相等的，也要弹出，因为下标不一样）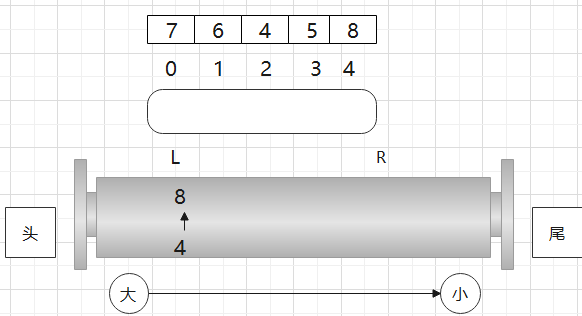
  3.      - ![image.png](https://cdn.nlark.com/yuque/0/2021/png/2817263/1634451226905-4882e4eb-f85e-41ba-9c8a-91219bf57bfd.png#clientId=u269902c4-5812-4&from=paste&height=280&id=ued2452e6&margin=%5Bobject%20Object%5D&name=image.png&originHeight=316&originWidth=582&originalType=binary&ratio=1&size=21047&status=done&style=none&taskId=u104b1b65-1d56-48db-a089-a7d79a1ff6d&width=515)

到这里最大值的更新结构就好了，那么最小值的更新结构就是反过来呗，维护一个从小到大的双端队列

  • 分析下复杂度

    • 窗口在数组上滑动，任何一个i位置最多进双端队列一次，出双端队列一次，
      • 任何数都会从尾巴进一次
      • 任何数会因为后面尾部要进来的数把它从尾部淘汰出去 或者 它自己从头部出去
    • 如果你划过了N个数，那么双端队列调整代价就是O(N)
    • 那么平均下来每次获取最大值的代价就是O(1)

  • 注意点：

    • 双端队列里放的是位置，不是放值，因为放位置我既可以拿到值，也可以判断过期没过期

题目：剑指Offer-59-I.滑动窗口的最大值


假设一个固定大小为W的窗口， 依次划过arr， 返回每一次滑出状况的最大值 image.png

先让窗口长到3长度，然后记录最大值，每次扩一数，缩一数，记录最大值，就ok了呀，我们的更新结构非常灵活，这还属于阉割版的呢

答案数组的长度 N - W + 1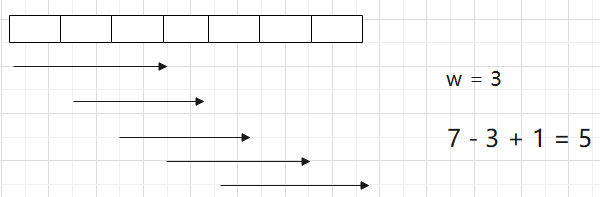
image.png

过期下标 R - W
比如来到0位置，那么就是-3就是过期下标，比如R到了3，那么0就是过期下标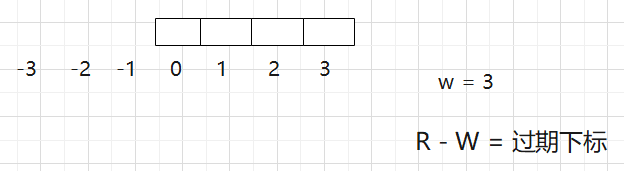
image.png

 public static int[] getMaxWindow(int[] arr, int w) {
        if (arr == null || w < 1 || arr.length < w) {
            return null;
        }
        LinkedList<Integer> qmax = new LinkedList<>();
        int[] ans = new int[arr.length - w + 1];
        int index = 0;
        for (int R = 0; R < arr.length; R++) {
            // arr[R] 只能放在比它大的数后面
            while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[R]) { // 当前让 i -> [i] 进窗口 ， i 就是 R
                qmax.pollLast();
            }
            qmax.addLast(R);

            // 如果窗口没有形成w的长度， 是不弹出数字的
            if (qmax.peekFirst() == R - w) {
                qmax.pollFirst();
            }
            // 开始记录
            if (R >= w - 1) {
                ans[index++] = arr[qmax.peekFirst()];
            }
        }
        return ans;
    }

题目二：AllLessNumSubArray

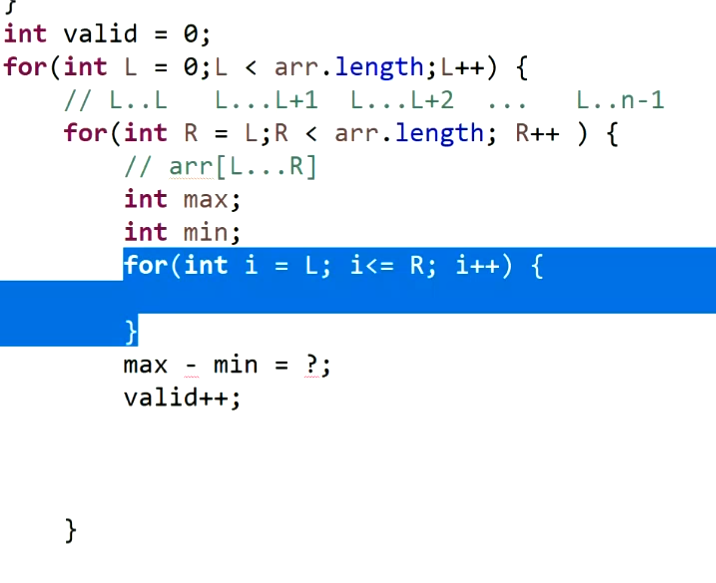
给定一个整型数组arr， 和一个整数num 某个arr中的子数组sub， 如果想达标， 必须满足： sub中最大值 - sub中最小值 <= num f返回arr中达标子数组的数量

  • 暴力解是O(N^3)

image.png

  • 用滑动窗口可以O(N) （因为窗口是只进不退的）

    <br />先不管滑动窗口，先看几个结论

  • 1） 如果数组arr[L … R]已经达标了，那么它内部任意一个子数组必达标

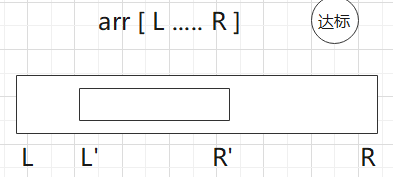
    • image.png
      • 因为小范围上的最大值一定比大范围上的最大值要小，

小范围上的最小值一定比大范围上的最小值要大

  - 所以必达标啊
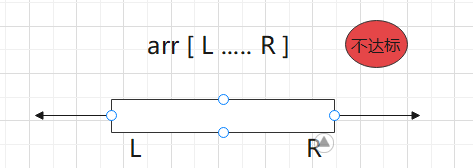
  • 2） 如果数组arr[L .. R] 已经不达标了，那么它再往怎么扩也是不达标的
    • 差值更悬殊了
    • image.png
  • 接下来看这道题怎么做
  • 需要两个双端队列，分别是最大值和最小值的更新结构
  • 每次窗口进一个位置，就问两个队列达标不达标，若达标，则窗口继续扩，直到不达标，停

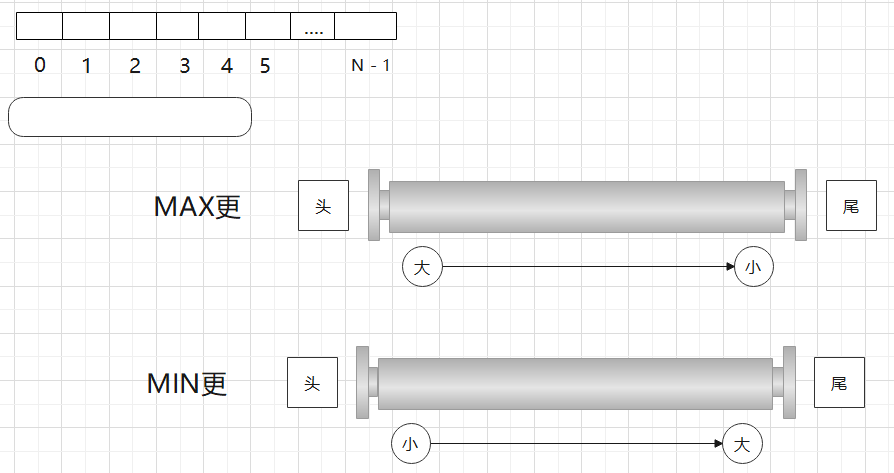
image.png
比如到到5就停了，那么以0为开头的子数组达标多少个？
0~0
0~1
0~2
0~3
0~4
总共 4 - 0 + 1 = 5个
然后我让窗口缩一下，看看两个队列过期没，继续这个流程，就求出了1位置开头的子数组中达标的有多少个，周而复始
。。。。
。。
。
最后就求出了所有位置开头的答案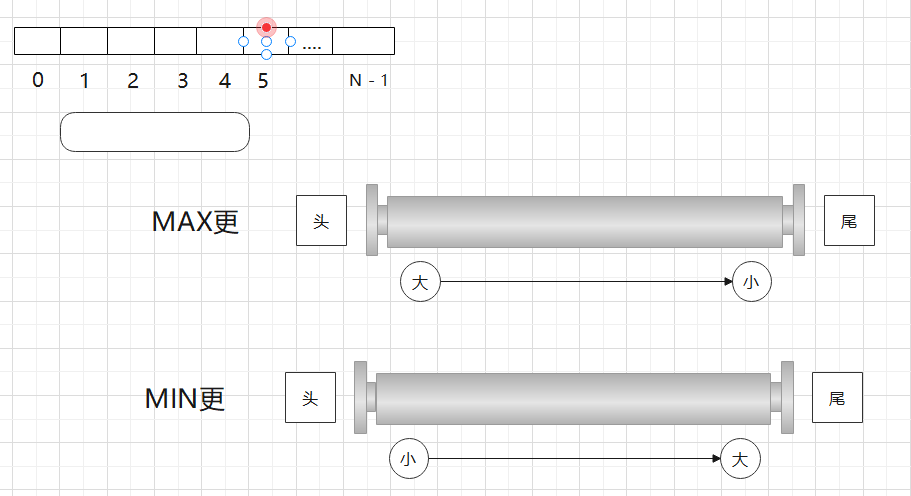
image.png

理解核心思想

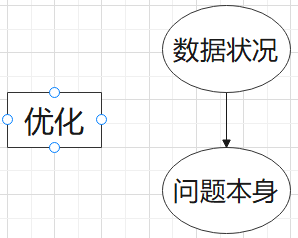
image.png
1） 数据状况
2） 问题本身
因为我们发现只要一个数组达标了，它内部必达标
只要一个数组不达标了，它再怎么扩也不达标，
这就把数据状况和问题本身建立起了单调性

然后我们是要求以每个位置开头的所有情况

这就是问题本身的单调性和窗口的滑动轨迹联系起来了

想到它的流程可以用窗口的滑动轨迹来写，进而使用到它的最大最小值更新结构

 public static int getNum(int[] arr, int num) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        LinkedList<Integer> qmax = new LinkedList<>();
        LinkedList<Integer> qmin = new LinkedList<>();
        int res = 0;
        // [L, R)左闭右开   [0,0)  [1,1) --> 窗口内无数
        int L = 0;
        int R = 0;
        while (L < arr.length) { // 尝试每一个开头
            while (R < arr.length) { // R向右扩到违规为止
                while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[R]) {
                    qmax.pollLast();
                }
                qmax.addLast(R);
                while (!qmin.isEmpty() && arr[qmin.peekLast()] >= arr[R]) {
                    qmin.pollLast();
                }
                qmin.addLast(R);
                if (arr[qmax.getFirst()] - arr[qmin.getFirst()] > num) {
                    break;
                }
                R++;
            }
            // R是第一个不达标的位置
            res += R - L;
            if (qmax.peekFirst() == L) {
                qmax.pollFirst();
            }
            if (qmin.peekFirst() == L) {
                qmin.pollFirst();
            }
            L++;
        }
        return res;
    }