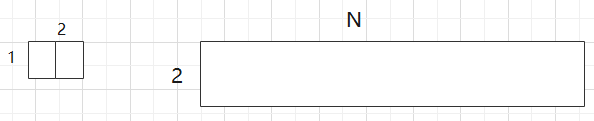image.png

快速幂

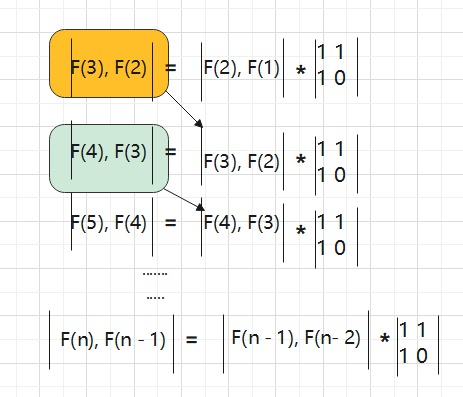
斐波那契数列的递推式是严格的递归式，不随条件转移的，那么就有如下线性代数的解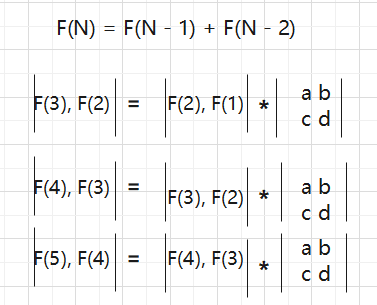
image.png

image.png
接下来就可以求出a、b、c、d了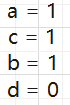
image.png
所以这个行列式就求出来了，接下来就来验证一下是不是每次都是这个行列式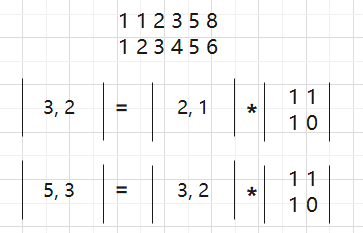
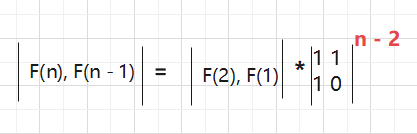
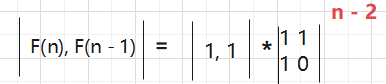
image.png
看来是的。

image.png
最终，
image.png
image.png
接下来的问题也就是一个矩阵的n次方能算得有多快整体就有多快了

快速幂 我们先看一个数的n次方怎么算得尽量快，举个例子比如10^75

image.png

所以t总共乘了几次呢？ 最多log2 75

所以矩阵也是一样
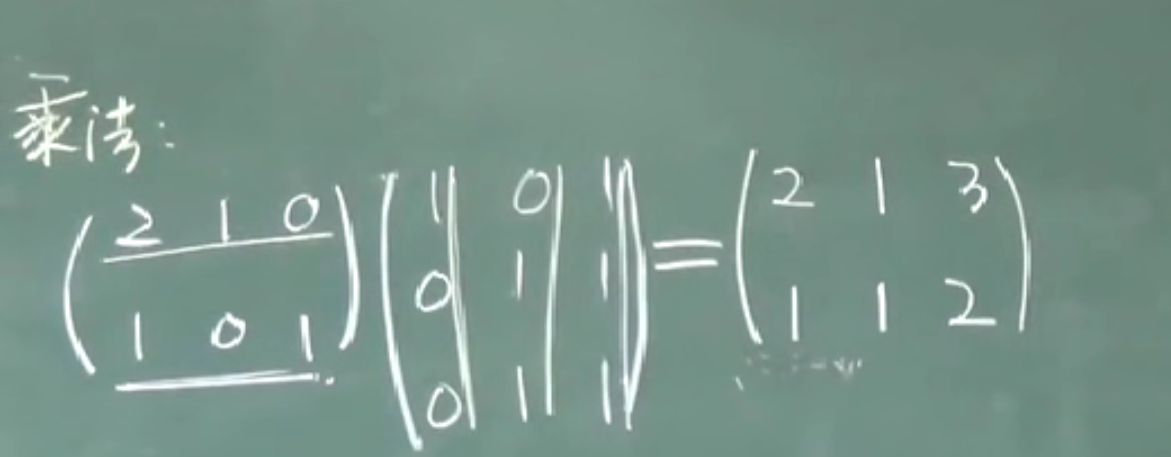
image.png

image.png
矩阵乘法就是第一个矩阵的行跟第二个矩阵的列对应元素相乘最后相加，
2 1 + 10 + 0*0就是结果中的左上角
image.png

  1.    // 递归
  2. public static int f1(int n) {
  3.     if (n < 1) {
  4.         return 0;
  5.     }
  6.     if (n == 1 || n == 2) {
  7.         return 1;
  8.     }
  9.     return f1(n - 1) + f1(n - 2);
  10. }
  1. // O(n)解法
  2. public static int f2(int n) {
  3.     if (n < 1) {
  4.         return 0;
  5.     }
  6.     if (n == 1 || n == 2) {
  7.         return 1;
  8.     }
  9.     int ppre = 1;
  10.     int pre = 1;
  11.     int cur = 0;
  12.     for (int i = 3; i <= n; i++) {
  13.         cur = ppre + pre;
  14.         ppre = pre;
  15.         pre = cur;
  16.     }
  17.     return cur;
  18. }
  1.  // logn解法
  2. public static int f3(int n) {
  3.     if (n < 1) {
  4.         return 0;
  5.     }
  6.     if (n == 1 || n == 2) {
  7.         return 1;
  8.     }
  9.     int[][] base = {
  10.         {1, 1},
  11.         {1, 0}};
  12.     int[][] res = matrixPower(base, n - 2);
  13.     return res[0][0] + res[1][0];
  14. }
  16. private static int[][] matrixPower(int[][] m, int p) {
  17.     int[][] res = new int[m.length][m[0].length];
  18.     for (int i = 0; i < res.length; i++) {
  19.         res[i][i] = 1;
  20.     }
  21.     int[][] t = m; // 矩阵的1次方
  22.     for (; p != 0; p >>= 1) {
  23.         if ((p & 1) != 0) {
  24.             res = muliMatrix(res, t);
  25.         }
  26.         t = muliMatrix(t, t);
  27.     }
  28.     return res;
  29. }
  31. // 两个矩阵乘完之后的结果返回
  32. public static int[][] muliMatrix(int[][] m1, int[][] m2) {
  33.     int[][] res = new int[m1.length][m2[0].length];
  34.     for (int i = 0; i < m1.length; i++) {
  35.         for (int j = 0; j < m2[0].length; j++) {
  36.             for (int k = 0; k < m2.length; k++) {
  37.                 res[i][j] += m1[i][k] * m2[k][j];
  38.             }
  39.         }
  40.     }
  41.     return res;
  42. }

扩展

image.png
只要C1~Cz，和k都是常数，它们就有logN的解
K为几就是几阶问题

奶牛问题

只有母牛没有公牛，一个农场第一年只有一头母牛，每只母牛每年严格只会产一只小母牛，所有牛都不会死，而且牛长到第三年就可以帮着继续生母牛， 求n年后牛的数量

image.png
F（N） = F(N - 1) + F(N - 3)

F(N)是今年的牛
F(N - 1)是去年的牛数量 （因为所有牛都不会死，所以去年的牛会保留的今年）
F(N - 3)是三年的牛数量 （牛三年才成熟）

它最后减的数字是几就是几阶问题，这就是个3阶问题，相当于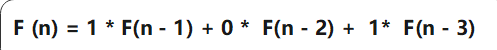
image.png
3阶问题就有这样的解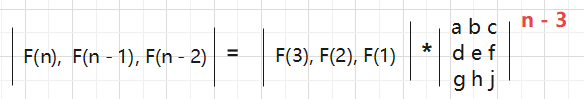
image.png

把这个矩阵解出来，就是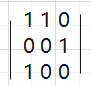
image.png

  1. // 奶牛问题
  2.     // 递归
  3. public static int c1(int n) {
  4.     if (n < 1) {
  5.         return 0;
  6.     }
  7.     if (n == 1 || n == 2 || n == 3) {
  8.         return n;
  9.     }
  10.     return c1(n - 1) + c1(n - 3);
  11. }
  1. // O(n) 
  2. public static int c2(int n) {
  3.      if (n < 1) {
  4.          return 0;
  5.      }
  6.      if (n == 1 || n == 2 || n == 3) {
  7.          return n;
  8.      }
  9.      int cur = 3;
  10.      int pre = 2;
  11.      int ppre = 1;
  12.      int tmp = 0;
  13.      for (int i = 4; i <= n; i++) {
  14.          tmp = cur;
  15.          cur = cur + ppre;
  16.          ppre = pre;
  17.          pre = tmp;
  18.      }
  19.      return cur;
  20.  }
  1. // O（logn）
  2. public static int c3(int n) {
  3.     if (n < 1) {
  4.         return 0;
  5.     }
  6.     if (n == 1 || n == 2 || n == 3) {
  7.         return n;
  8.     }
  9.     int[][] base = {
  10.         {1, 1, 0},
  11.         {0, 0, 1},
  12.         {1, 0, 0},
  13.     };
  14.     int[][] res = matrixPower(base, n - 3);
  15.     return 3 * res[0][0] + 2 * res[1][0] + 1 * res[2][0];
  17. }
  19. private static int[][] matrixPower(int[][] m, int p) {
  20.     int[][] res = new int[m.length][m[0].length];
  21.     for (int i = 0; i < res.length; i++) {
  22.         res[i][i] = 1;
  23.     }
  24.     int[][] t = m; // 矩阵的1次方
  25.     for (; p != 0; p >>= 1) {
  26.         if ((p & 1) != 0) {
  27.             res = muliMatrix(res, t);
  28.         }
  29.         t = muliMatrix(t, t);
  30.     }
  31.     return res;
  32. }
  34. // 两个矩阵乘完之后的结果返回
  35. public static int[][] muliMatrix(int[][] m1, int[][] m2) {
  36.     int[][] res = new int[m1.length][m2[0].length];
  37.     for (int i = 0; i < m1.length; i++) {
  38.         for (int j = 0; j < m2[0].length; j++) {
  39.             for (int k = 0; k < m2.length; k++) {
  40.                 res[i][j] += m1[i][k] * m2[k][j];
  41.             }
  42.         }
  43.     }
  44.     return res;
  45. }

爬楼梯问题

跟斐波那契数列差不多，那个矩阵是一样的，只不过初始项不一样而已

  1. // 爬楼梯问题
  2. public static int s1(int n) {
  3.     if (n < 1) {
  4.         return 0;
  5.     }
  6.     if (n == 1 || n == 2) {
  7.         return n;
  8.     }
  9.     return s1(n - 1) + s1(n - 2);
  10. }
  12. public static int s2(int n) {
  13.     if (n < 1) {
  14.         return 0;
  15.     }
  16.     if (n == 1 || n == 2) {
  17.         return n;
  18.     }
  19.     int res = 2;
  20.     int pre = 1;
  21.     int tmp = 0;
  22.     for (int i = 3; i <= n; i++) {
  23.         tmp = res;
  24.         res = res + pre;
  25.         pre = tmp;
  26.     }
  27.     return res;
  28. }
  30. public static int s3(int n) {
  31.     if (n < 1) {
  32.         return 0;
  33.     }
  34.     if (n == 1 || n == 2) {
  35.         return n;
  36.     }
  37.     int[][] base = { { 1, 1 }, { 1, 0 } };
  38.     int[][] res = matrixPower(base, n - 2);
  39.     return 2 * res[0][0] + res[1][0];
  40. }

题目ZeroLeftOneStringNumber

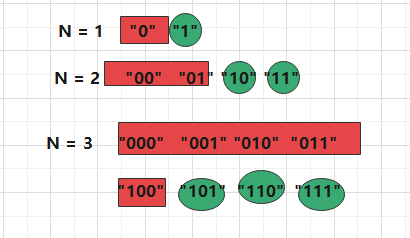
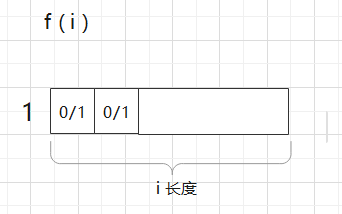
image.png
image.png
image.png
递归f（i）含义：
i长度，但是左边必然有一个1， 可以认为这个假想的1必然存在在i长度的左边， 问你i长度可以自由变换，最终整体达标多少个

比如我N = 8， 我怎么调？ 我调f （7）， 因为最左边必须得有1个1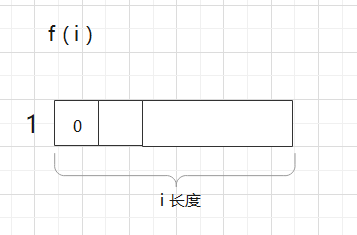
image.png
如果圆圈里第一个数填0， 那么第二个数还能填0么？不能，必不合法
所以第二数只能1， 然后就让 i- 2长度任意去变

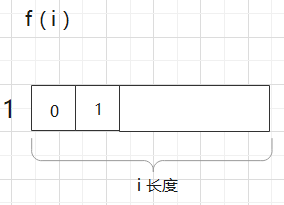
  1.   ![image.png](https://cdn.nlark.com/yuque/0/2021/png/2817263/1633938840976-dcb2300c-0783-4feb-b4ca-148908a4560f.png#clientId=u8b92b561-2a7e-4&from=paste&height=196&id=u08e580fa&margin=%5Bobject%20Object%5D&name=image.png&originHeight=205&originWidth=284&originalType=binary&ratio=1&size=6896&status=done&style=none&taskId=u54f7dfd2-2ea3-49be-8d97-b8fa5d11922&width=272)

如果第1个数填的是1， 那么就让i- 1的长度任意去变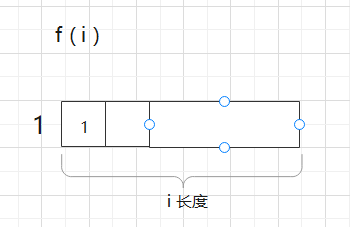
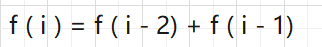
image.png
image.png

这是什么？斐波那契数列啊，这又是敏感度的问题，但这是什么尝试？ 从左往右尝试的模型

  1.  // ZeroLeftOneStringNumber
  2. // 递归
  3. public static int getNum1(int n) {
  4.     if (n < 1) {
  5.         return 0;
  6.     }
  7.     return process(1, n);
  8. }
  10. private static int process(int i, int n) {
  11.     if (i == n - 1) {
  12.         return 2;
  13.     }
  14.     if (i == n) {
  15.         return 1;
  16.     }
  17.     return process(i + 2, n) + process(i + 1, n);
  18. }
  1. // O(n)
  2. public static int getNum2(int n) {
  3.     if (n < 1) {
  4.         return 0;
  5.     }
  6.     if (n == 1 || n == 2) {
  7.         return n;
  8.     }
  10.     int pre = 1;
  11.     int cur = 2;
  12.     int tmp = 0;
  13.     for (int i = 3; i <= n; i++) {
  14.         tmp = cur;
  15.         cur = pre + cur;
  16.         pre = tmp;
  17.     }
  18.     return cur;
  19. }
  1. // O(logn)
  2. public static int getNum3(int n) {
  3.     if (n < 1) {
  4.         return 0;
  5.     }
  6.     if (n == 1 || n == 2) {
  7.         return n;
  8.     }
  9.     int[][] base = {{1, 1}, { 1, 0}};
  10.     int[][] res = matrixPower(base, n - 2);
  11.     return 2 * res[0][0] + res[1][0];
  12. }

题目：瓷砖

有一个2 x N的区域，然后我只给你1 x 2的瓷砖，问你用这种瓷砖把这个区域填满一共有多少种方法？ image.png

F（N）： 如果你还剩一个2xN的干干净净的区域还没有填满，请你返回方法数
第一种情况: 瓷砖竖着放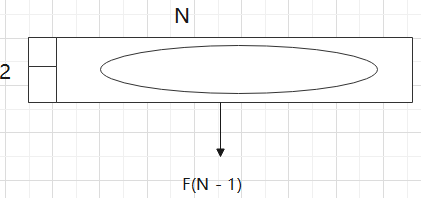
image.png

第二种情况：瓷砖横着放，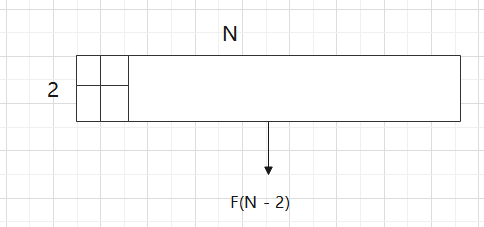
image.png

所以F(N ) = F(N - 1) + F(N - 2)