0 Background

对于常见的参数模型，其中输⼊到输出的映射的形式由可调节参数构成的向量控制。包括之前提过的线性基函数模型和神经网络模型，都包含一个显示的学习阶段：使用⼀组训练数据⽤来得到参数向量的点估计，或者⽤来确定这个向量的后验概率分布。然后，训练数据之后被丢弃，对于新输⼊的预测仅依靠学习到的参数向量。
在非参数化方法中，曾介绍过一种称为核密度估计的分类方法：由“核”函数的线性组合构成的Parzen概率密度模型，其中每⼀个核函数都以训练数据点为中⼼。类似的还有最近邻⽅法，把每个新的测试向量分配为训练数据集⾥距离最近的样本的标签。由于训练数据点或者它的⼀个⼦集会被保留并在预测阶段被使⽤，因此这类方法称为基于存储 （memory-based）的方法。通常需要⼀个度量，来定义输⼊空间任意两个向量之间的相似度，这种方法特点是通常“训练”速度很快（无显示的训练过程），但是对测试数据点的预测速度很慢。

0.1 kernel function

核函数是这类基于存储的方法的核心，预测阶段正是使用了训练数据点处计算得到的核函数的线性组合。对于基于固定非线性基函数映射的模型而言，核函数的形式如下

这里的用来表示训练集中的样本，不难看出核函数具有对称性。根据这个式子，我们可以将核函数初步看作是特征空间的内积。很多线性参数模型都能被转化为一个形如上式的“对偶表示”形式。并且，使用核方法还能对很多现有的算法进行有趣的扩展。

0.2 keywords

• 势函数？
• 核函数：常见的核函数、核函数性质与构造方法
• 对偶表示

  1 对偶表示

  许多线性回归模型与线性分类模型都能表示为这种对偶形式，因此能自然得等价表示为核函数的形式。这里以正则化的线性基函数回归模型为例，我们知道其参数的最大似然估计等价于最小化正则化的平方和误差函数，如下所示
  
  令误差函数关于模型参数的梯度为零，得最大似然的解析解
  
  其中，是设计矩阵，其第n行对应第n个样本在特征空间中的基函数向量，而，表示经常量调整后的误差值，因此可将看作训练集中N个样本的输入经过基函数的非线性变换后，以预测误差的大小为权重进行加权求和所得。
  按照这种表示方法，我们重写（2）中的误差函数，可得
  
  其中是Gram矩阵，是一个N×N的对称矩阵，矩阵中元素为。因此，对应的线性回归模型重新写为
  
  注意到上式中的变量和仅与核函数相关，因此我们完全使用核函数对线性基函数回归模型进行了等价表示，这称为对偶公式。注意到为训练数据中各个样本的目标值，模型预测值由经过加权求和得到，因此从核函数的角度看待线性回归基函数模型——任意输入样本的预测值将由训练数据的目标值的线性组合给出。

  2 构造核

  为了利用核替换，我们需要构造合法的核函数。

  2.1 合法性

  在不需要显示地构造特征函数的前提下，简单验证某函数是否为合法核函数的充要条件是Gram矩阵（元素为）在任意的集合下都是半正定的。

  2.2 构造方法

  构造新的核函数的一个有效方法是使用简单的核函数作为基本的模块，然后利用以下的性质来构造更为复杂的核函数。

  2.2.1 核函数变换性质

  给定合法的核与，则经过下列变换得到的新核也是合法的
  
  其中是常数，是任意函数，是系数非负的多项式，是将映射到下的一个变换，则是下的一个合法的核，是对称的半正定矩阵，变量则满足，和同样是各自空间下的合法核函数。

2.2.2 基本核函数

线性核

多项式核

高斯核

不难发现多项式核函数与高斯核函数都是由线性核函数结合上面提到的基本性质得到的。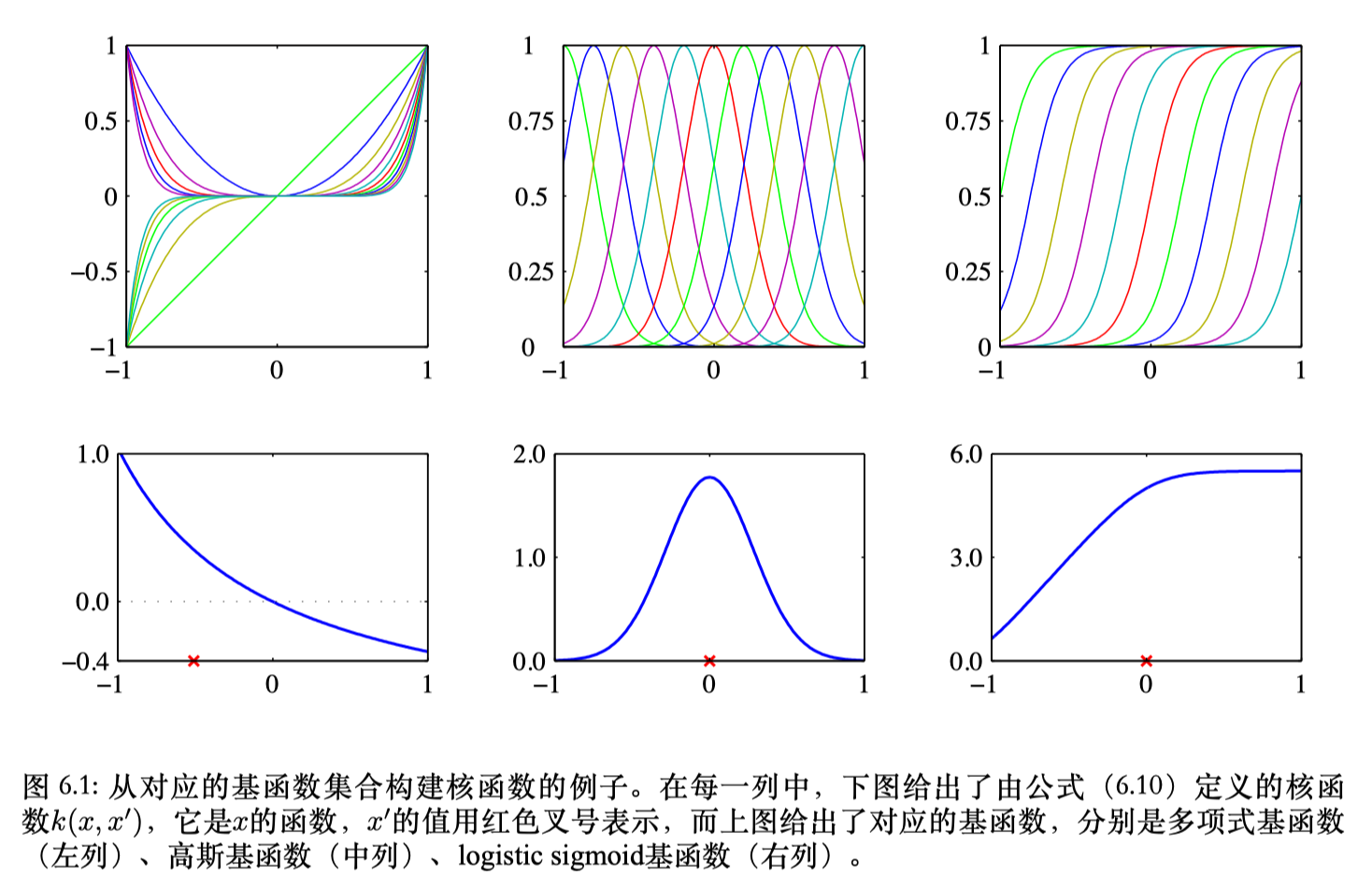

2.2.3 符号输入

核观点的一个重要功能是可以将模型的输入扩展到符号化输入的范畴，如图片、集合、文本等等，而不再局限于实数向量。
例如，定义一个非向量空间，这个空间由指定集合的所有可能的子集所构成，那么一个简单的合法核可以是
其中表示这两个子集的交集，则表示集合A中的元素数量。

*2.2.4 生成式构造

*3 径向基函数网络

4 高斯过程

我们已经通过将对偶性的概念应⽤于回归的⾮概率模型，引出了核的概念。这⾥我们把核推⼴到概率判别式模型中，引出⾼斯过程的框架。在⾼斯过程的框架里，我们抛弃参数模型，直接定义函数上的先验概率分布。乍⼀看来，在函数组成的不可数的⽆穷空间中对概率分布进⾏计算似乎很困难。但是，针对⼀个有限的训练数据集，我们只需要考虑训练数据集和测试数据集的输⼊处的函数值即可，因而可以在有限的空间中进⾏计算。
等价于⾼斯过程的模型在许多不同领域被⼴泛研究。例如，ARMA（⾃动回归移动平均）模型、Kalman（卡尔曼）滤波以及径向基函数⽹络都可以被看成⾼斯过程模型的形式。

*4.1 随机过程

在概率论中，我们研究了随机变量、n维随机向量，在极限定理中我们研究了无穷多个随机变量，但只局限在它们之间相互独立的情形。如果将上述情形加以推广，随机过程研究的则是：一族无穷多个、相关的随机变量。
对于一个随机变量，其概率分布由某些参数完全确定，表示为。扩展到一个概率空间中：对于每一个特定的参数，是定义在概率空间中的一个随机变量，我们称随机变量族为该概率空间上的一个随机过程，其中是一个参数集，一般表示时间或空间，当其为可列集时，一般将对应的随机过程称为随机序列。

• 固定时，是定义在样本空间上的函数，为一随机变量；
• 固定时，是一个关于的样本函数，或称为随机过程的一次实现；

4.2 线性回归的随机过程角度

一个线性基函数回归模型，由M个固定的基函数的线性组合所确定，即

假定模型参数的先验概率分布是各向同性的高斯分布，各向均值为0，方差由统一的超参数所控制，形式如下

对于一组大小为N的训练数据，各样本的回归预测值为，若将预测值的集合记作向量，则有

其中为N×M的设计矩阵，每行由样本对应的M维基函数向量组成。此时的是由服从高斯分布的参数通过设计矩阵变换得到，而矩阵变换对应于一个唯一的线性变换，因此也服从多元高斯分布，可由其均值和协方差矩阵完全确定

就是N×N的Gram矩阵，矩阵中元素为，由核函数完全定义。这样，整个训练集对应的预测值联合服从一个多元高斯分布，为一随机过程，称为高斯随机过程。由于对其均值无任何先验知识，假定为对称的0均值，等价于基函数的观点中令权值的先验概率分布均值为零。在此假设下，高斯过程将完全由协方差确定。

4.3 用于回归的高斯过程

1. 构建训练集上数据点的联合概率分布模型；
2. 关于新的待预测输入，构建新的联合分布；
3. 通过贝叶斯定理计算待预测数据点的条件概率分布；

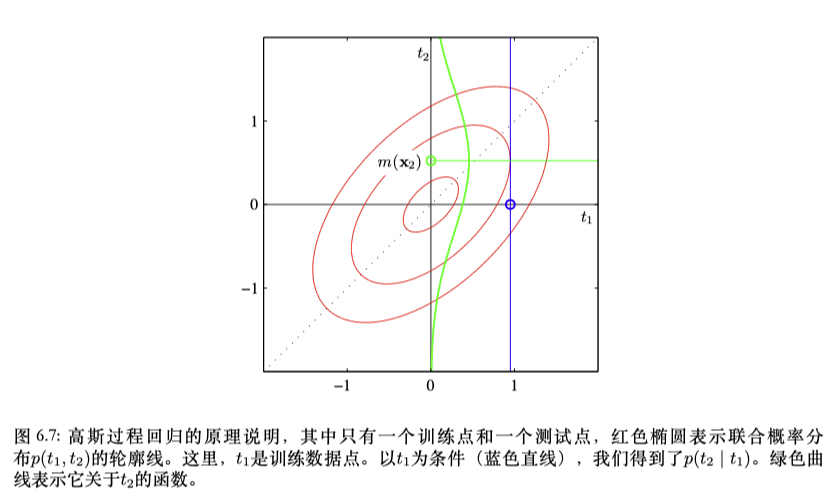
TODO