1 引入：多项式曲线拟合

• 关键词：模型空间、模型参数、泛化性

不同阶数M的多项式拟合假设，引出了模型选择和过拟合问题：在数据拟合误差一致的情况下，过高的模型复杂度常常预示着过拟合；
在简单的多项式拟合中，一旦模型假设完成，通常认为模型的参数规模及复杂度就不变了，但我们更希望模型能根据问题的复杂度（训练样展现的复杂性）来自动调整自身的复杂度，在拟合样本的情况下尽量满足剃刀原理。引入控制“有效模型参数”的方法：

• 正则化系数，通过收缩系数值减少模型中起作用的参数。正则后的参数求解相当于条件最优化过程，当拟合误差相同时，选择模型参数和(正则项)最小的结果，降低了模型的复杂度和确定性。
• 贝叶斯模型，参数的有效数量根据数据集的规模进行调整，数据集小则更依赖于先验；**

2 概率论

• 如何量化数据中的不确定性？
• 如何基于不确定性函数来进行参数估计？

  统计模式识别的核心：使用数据进行概率分布建模

2.1 基本规则

sum rule:
product rule:
Bayes’ theorem：

2.2 随机变量类型与其概率函数

• 连续变量：概率密度函数;
• 离散变量：概率质量函数；

（同样遵循基本的概率规则，只是运算方式有所区别，连续变量的sum rule需要使用到积分）

2.3 贝叶斯概率

对于一个随机变量(事件)，基于经验或其他基础理论设定先验概率描述其不确定性，再根据新的证据来修正先验假设，使得随机变量的分布更加贴近训练数据集，先验概率转化为后验概率。相比于频率学派，贝叶斯概率理论的优缺点如下

• 优点
  • 呈现模型参数本身的不确定性，为模型选择提供依据；
• 缺点
  • 在整个参数空间中进行分布求解十分困难；
  • 样本有限的情况下，十分依赖于先验概率的选择；

不妨先将总体看做无限维的向量，不同的参数构建了一个无限维度的向量空间。从中取出N个样本构成有限维的样本向量，在足够复杂的情况下，是存在两个不同的和使得。
概率派将总体中的未知参数看做固定值，因此在求解参数的时候认为参数空间中能使样本出现概率(数据集联合概率)最大的参数即为真实参数，且样本越多这种求解就越准确。贝叶斯派的做法没有这么“激进”，考虑实际样本是真实样本和噪声的混合体，并且样本的数量总是有限的，不同的都存在产生同一份样本的可能性，只是相对大小不同，但可能数据集D正是出自某个小概率参数事件（由于某些样本上的噪声干扰），贝叶斯派不否认这种可能性，并将这种不确定性代入到参数的估计中，只是不断用样本调整参数对应的概率分布，缺点显然是这种参数分布的取值空间实在太大，计算量急剧上升。

2.4 参数点估计：极大似然与最大后验

书中以高斯分布的参数估计为例，利用样本估计高斯分布的均值和方差：

极大似然估计 MLE

1. 假设总体分布，确认分布参数；
2. 假设样本i.i.d，划定数据集；

3. 计算样本联合概率，得到似然函数，利用似然函数进行参数估计；

   

4. 求使得(对数)似然函数最大的参数值，即样本集合出现的联合概率最大化；

   • 问题：存在方差低估问题，尤其是样本量偏小时，方差将以的程度偏移；（体现在同一样本数量N的情况下，对总体进行多次采样估计的平均情况下，估计出的方差总是偏小的。当然在样本数N极大时，该方法的方差估计值还是与真实值相合的）

对于开头中的曲线拟合问题，按照极大似然的思路可得如下似然概率：

极大似然估计中的似然函数其实隐含着一个前提：假设总体分布的参数为，那么当我们已知时，该样本对应的值就由唯一确定了。
实际中，由于样本是人为评判、测量、记录的，必然存在一定程度的误差，也就引入了噪声，带来了额外的不确定性。如果尝试引入随机噪声并进行建模(高斯白噪声)，假定样本之间的采样方式基本相同，可认为该方差在不同样本之间表现为同一“背景噪声”。假设为样本值，为真实值，有，其中对应该高斯噪声的方差的导数，先称为精度参数。
假设模型为，其中为模型的未知参数，模型预测的目标是真实值，即。给定x的值，y的样本值以真实值y’为均值呈正态分布，方差为。概率表示为：

进一步以此表示数据集整体的似然概率：

对数化该似然概率：

右式中仅有第一项和模型参数w相关，因此最大该对数似然函数等价于最小化，这与均方误差仅有常数项的差别。

也就是说，在高斯噪声的假设下，最大化似然函数等价于最小化均方和误差函数。

最大后验估计 MAP

我们知道，贝叶斯派的思想和频率派的基本假设是不同的：前者认为“事件的本体属性”是可知的，并以此建模，后者认为并非如此，我们对事件的认识是有局限性的，因此总会包含不确定性，但我们可以利用主观知识加上客观证据去“模拟”，不断接近真相。
基于不同的参数假设。频率学派认为模型的参数是未知但唯一确定的，我们需要拟合样本去接近这个“真相”；而贝叶斯派则认为参数本身就包含不确定性（类似物理中的测不准原理？），我们可以假设一个先验分布，根据样本值来调整先验分布，使调整后得到的后验分布更接近参数自身的分布。
比如在上面的最大似然曲线拟合基础上，我们假设参数服从某高斯先验分布，根据贝叶斯定理：

分母部分对于所有w一致，当我们需要找到最大的后验概率值时，只需要最大化分子即可：

取对数似然：

除去与参数w无关的常数项，等价于最小化，实际上就是加入了正则项的平方和误差函数。
以上提到的最大似然法MLE和最大后验法MAP均为点估计，区别在于MAP加入了参数本身的不确定性假设。但如果是纯粹的贝叶斯方法，需要通过对后验概率密度函数进行积分来进行概率表示。

2.5 两个问题

• 模型选择：模型超参数选择，如何在训练过程中就完成模型超参数的“调整”，远离过拟合等问题。
• 维度灾难：模型维度的可扩展性，从低维中推导出的理论在高维空间中很多并不适用。
  

3 决策论

• 如何基于计算出的不确定性信息进行“最优”决策？

问题：
如何以推断出的样本分布为基础，做出最佳的决策？
前提：
a. 我们需要一个能对决策产生的效果进行评价的标准；
b. 我们基于从训练数据中推断所得的样本分布进行决策的；
c. 通常推断所得的样本分布包含对真实分布的不确定性；

3.1 决策的目的

1）分类问题

1. 最小化分类错误率/最大化分类正确率

一个简单的二分类问题：用一些特征x来判断一个人是好人还是坏人，从训练中得到，我们需要要划定一个阈值：时认为这个人是好人，基于判定阈值与联合分布，可将x的取值空间划分为两部分：，可知：

为了最小化该分类错误率，我们需要是的覆盖较小的区域，且覆盖较小的区域，这就意味着当时，我们需要将该区域的x划分给，反之我们要将区域划分给。如下图所示，最终的分界线(决策面)为。

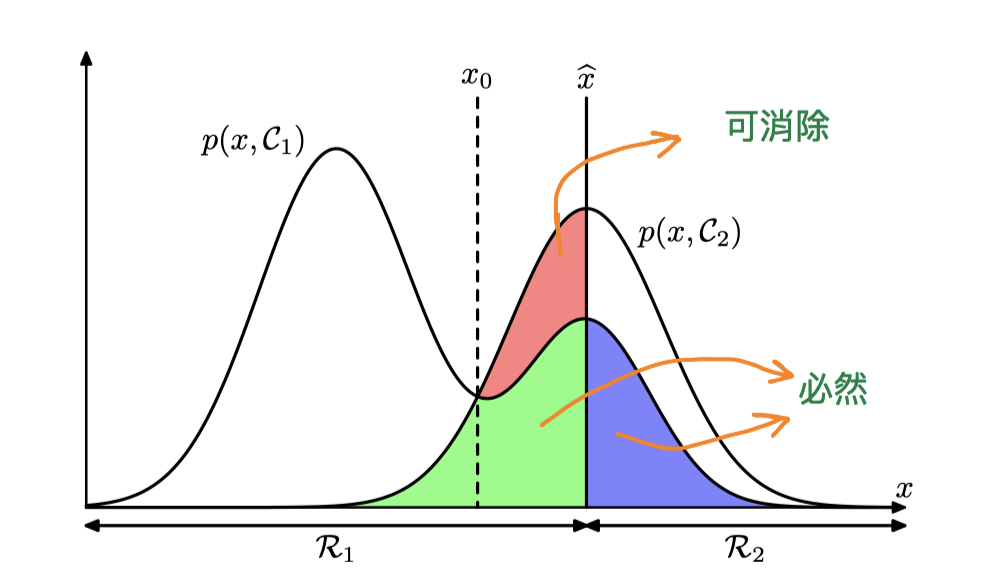
对于多分类问题，使用最大化分类正确率的方式会更方便：

2. 最小化期望损失

假如我们认为“人性本善”，除非证据十分“明显”否则不会轻易认定一个人为坏人。若模型将训练样本中的一个好人判定为坏人可看作“重大错误”，我们需要在计算错误率时赋予这类错误更大的权重。也就是将模型的评估函数进行调整，将这种将好人错分为坏人的情况提升“重要程度”：

对于已有的推断模型，我们可以通过调整决策时的阈值，将这种主观倾向性加入模型的决策中，使上述加权损失函数值达到最小。

tips 需要注意，决策时我们基于的是学习出的联合分布，如果估计出的联合分布与真实情况相差甚远，这里的最佳决策也就不靠谱了。

2）回归问题

对于回归问题，也有各种损失函数，以平方和损失函数为例。已推断出样本的联合概率，计算后验概率进行样本值预测，拟合真实样本值。通过变分法求解可知：

可以理解为数据内在的噪声，导致了样本的不确定性。基于包含噪声的样本进行模型预测时，使得(平方和)损失最小的解是受噪声影响下产生的条件分布的均值。因此，在已推断出条件概率的情况下，最佳的回归预测值为该条件概率的期望值。

如上式所示，利用期望函数对损失函数进行分解。当时第一项为0，期望损失可达最小值。第二项则是样本自身条件方差的期望，对应于由样本内部不确定性引入的噪声误差，不随模型预测改变。**

3.2 推断+决策 or 直接判别？

推断：从训练数据集中确认等。
决策：基于推断出的概率分布，作出最佳的“选择”。

根据模型的工作模式不同，进行如下分类：

1. 需要进行概率推断：

生成式模型：贝叶斯推断+决策。特点是对联合概率分布建模，得到的可用于样本生成；
判别式模型：推断+决策。对后验概率分布建模；

1. 无需进行概率推断：

判别函数(end to end?)：直接判别。直接将将输入映射为结果；
概率推断需要计算联合概率/后验概率，虽然需要额外的计算，但在很多情景下价值很大，如补偿类先验概率、组合模型、拒绝选项。

4 信息论

• 如何衡量真实与预测之间的差异？

  4.1 (离散)信息量

1. 信息量

随机变量/事件产生一个具体的结果时，所包含的“信息/惊讶程度”：；

1. 平均信息量——熵

随机变量不同状态下的信息量的期望值：；

1. 最短编码/无噪声编码理论

熵是传输一个随机变量状态值所需比特位的下界（以bit作为信息量单位）；

1. 最大化离散变量熵的分布式均匀分布；

4.2 连续信息量

1. 最大化连续变量熵的分布是高斯分布；
2. 条件熵

概率乘积关系表现为熵的加和关系，条件概率->附加信息量：

4.3 相对熵与互信息

相对熵/KL散度
正常情况下某个连续分布的熵为，当使用预测分布对真实分布下产生的样本进行编码，则为，其中表示按照对进行编码时所需的比特位，而则是在样本中的实际分布情况，按照这种方式编码得到的平均编码比特位无法达到最短编码，则多出的这部分编码比特位可称为平均附加信息量（当且仅当时以上的KL散度达到最小值0）：

注意到KL并非是对称的，，如果直接用作误差的评估函数，可能会带来一定问题。

KL散度的使用
a. 我们在数据压缩和概率密度估计时，使用模型对未知的真实分布进行建模估计时，一定会造成编码效率的损失;
b. 使用样本的KL散度近似表示总体的KL散度，以此衡量模型预测分布与真实分布之间的差距：

不难看出最小化该KL散度，等价于最大化对数似然函数。
[考虑到这里涉及样本的出现概率，通常更适合在分类问题中使用？]

c. 互信息：判断随机变量的独立性

不妨将表示为先验分布的信息量，则对应后验分布的信息量，互信息则是由于新样本的观测使得不确定性的减小（不确定性越大时信息量也越大）。

🤔 信息量与MLE、MAP？

当我们定义完了信息量和熵，回过头去看之前的最大似然参数估计，就变成了：“在给的定数据集样本下，先进行模型假设，再找到一组整体信息熵/不确定性最小的参数完成模型的构建”。

5 小结

在给定模型的情况下，纯粹的频率理论根据统计结果给出最有可能的参数选择，给出“最有可能”的参数选择，MLE是纯粹从样本上看的最大概率，MAP是结合和先验背景时的最大概率。而贝叶斯则使用统计数据调整先验分布，并保留这种概率分布的形式，描述不确定性。在实际决策时，我们才是真正“抛弃”不确定性

*思考

• 频率派和贝叶斯派最根本的区别是？