1 背景知识

1.1 泰勒展开

a. 目的

找到复杂函数的局部线性近似，并使用多项式函数的形式进行表示。

b. 原因

多项式函数易于计算，如求值、求导、求积分。。。并且易于对比和理解，相比于cos等函数。

c. 方法

前提：
函数的一阶导数几何意义：函数在某点附近的函数值变化率，即为切线的斜率；
函数的二阶导数几何意义：函数在某点附近的切线斜率的变换率，即曲线的弯曲方向和程度；
如果两条曲线f(x)和g(x)在某点x处的值一致，且二者在此处的切线相同，函数曲线的弯曲程度也相同，那么我们可以认为在该点处两条曲线是“近似”的。

思路：
我们使用一个k阶多项式去对一个余弦函数进行近似，令多项式为

按照前提中的思路，比如为了使得函数与余弦函数在点附近足够相似，要求函数值一致，且切线和弯曲程度也一致，得

由前三个约束式可知，因此是在处的一个合理的近似。当然，由于余弦函数可以无限次进行求导，也就是为了逼近，我们可以不断用高阶导数的一致性来约束，从而提高近似程度。

注意到，多项式中任意k次项的参数并不受到更高阶项的影响，比如高阶项，那么在k阶导数中，该高阶项对应于，这一项在处的值也为0，因此该高阶项会被“消去”。为了使得我们的多项式能在任意点对目标函数进行近似，将修改为如下形式

其中表示目标函数需要被近似表示的位置。对于任意的函数，只要其在任意点都能取到k阶导数，那我们就能使用这样一个多项式对其进行近似，因为当我们知道了这个函数的所有高阶导数，那我们几乎知道了关于这个函数一切信息。这被称为（k阶）泰勒展开式，通用形式如下

展开式里每项加入的阶乘项是为了多阶求导带来的系数累乘。因为假设我们要用这样一个r阶多项式函数在点处近似某目标函数，由于要求二者的k阶导相等，那么，注意到对于r阶的多项式函数求k次导后，低于k阶的项被消去了，而高于k阶的项由于也被消除，因此有，因此我们令。

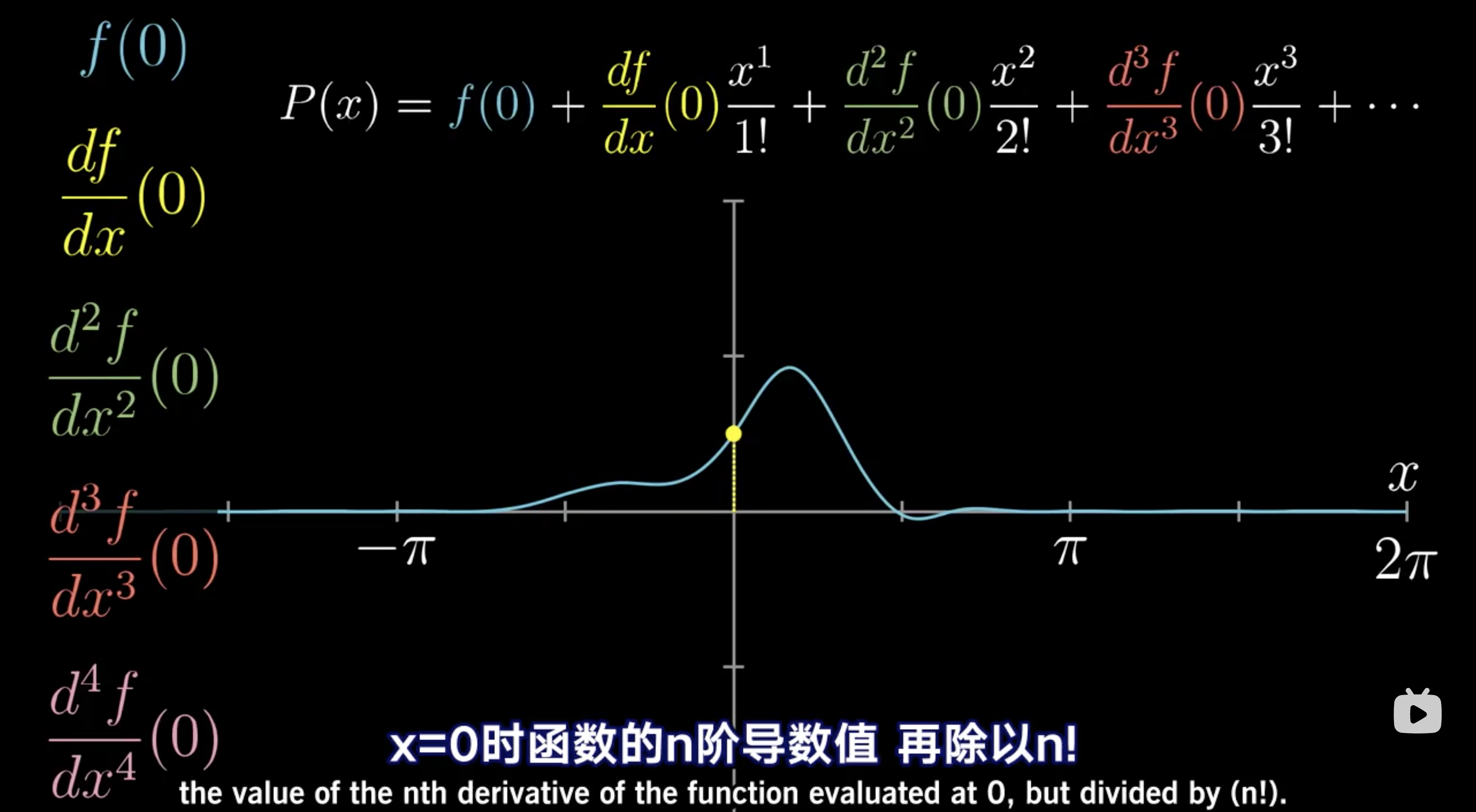
若多项式是有限个项的，则为泰勒多项式，若多项式被定义为无穷项的，则被称为泰勒级数，后者涉及到收敛问题。若某个函数泰勒级数是发散的，则在任意点处的泰勒级数会有一个收敛半径，而一旦泰勒级数的泰勒级数是收敛的，随着级数增大，在任意点处的泰勒展开式能无限逼近整个目标函数曲线！比如函数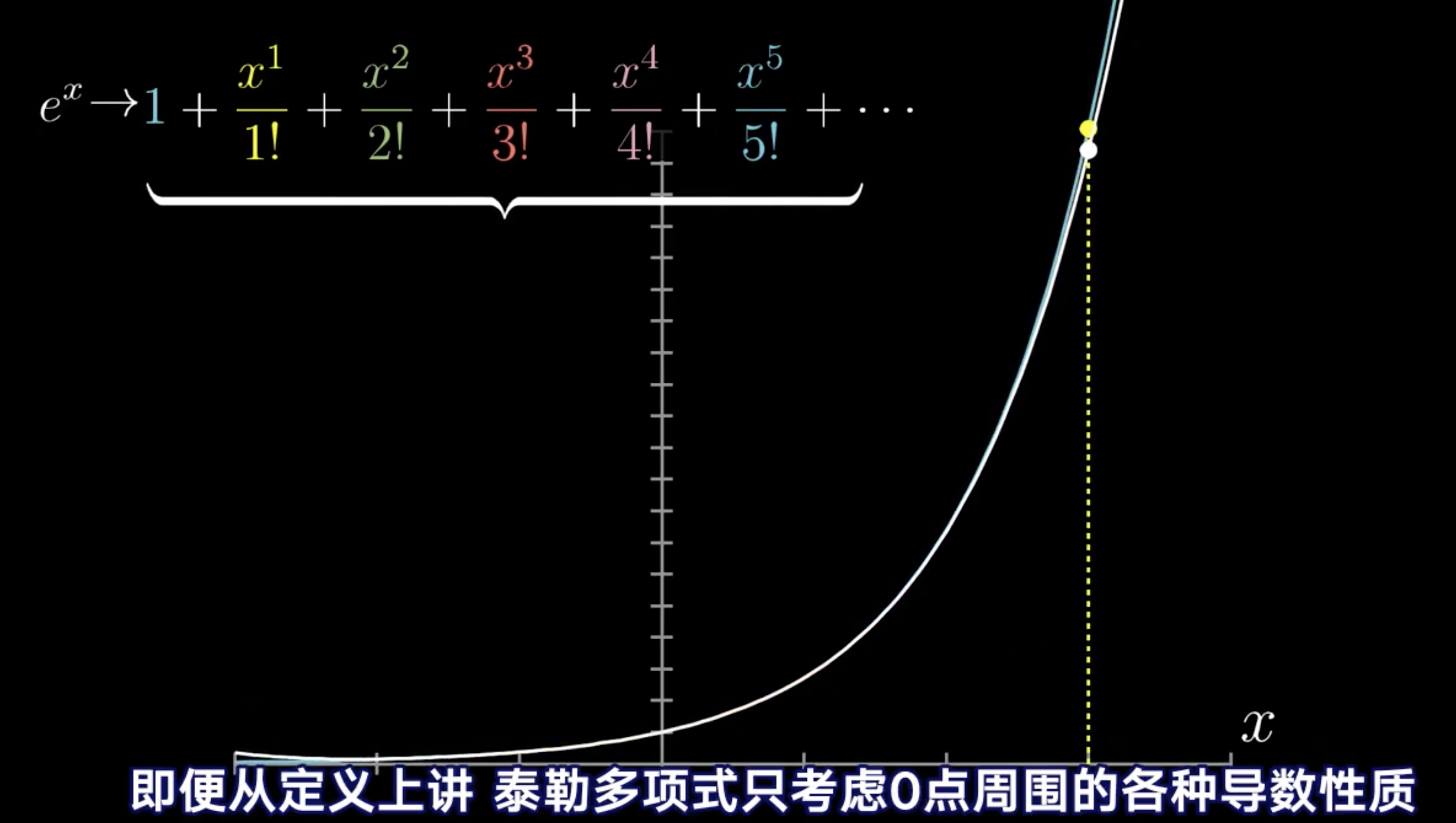

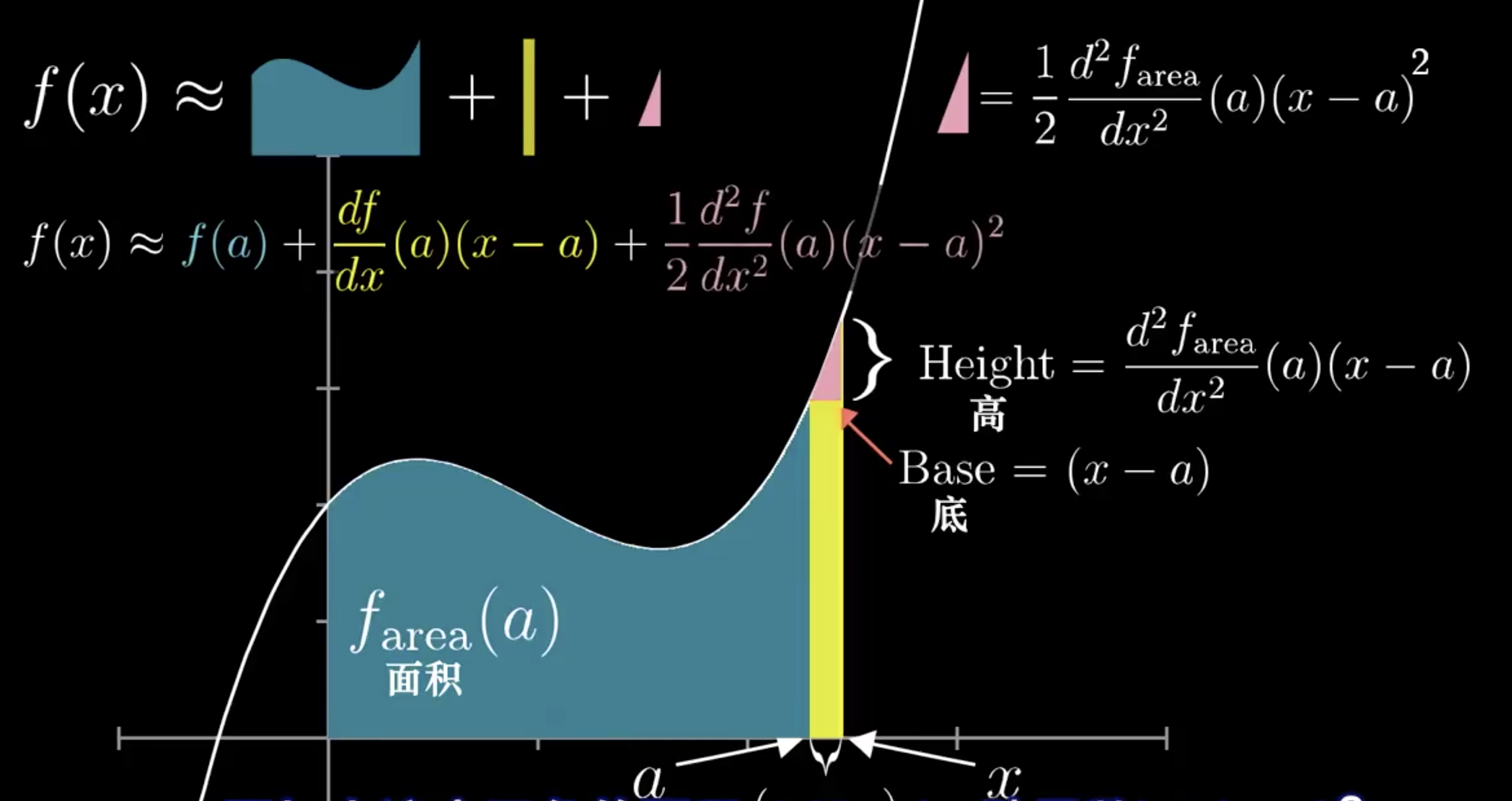
也可以从微积分几何含义的角度来看泰勒展开式（详见）。我们可将函数看作其导数的“面积函数”，对于某个点a，我们增加一个微小量，使其达到附近的点x。则新的面积函数可以按如下方式进行表示，不难发现这与泰勒展开式完全一致。注意这里所画出曲线对应的函数是。

2 Newton法

2.1 问题

求使得函数达到最小值的点。

2.2 基本假设

若在上具有连续的二阶偏导数，并且其Hessian矩阵正定（正定矩阵是可逆的），则可使用Newton法进行迭代求解。

2.3 解决思路

假设当前点位于，在该点处对函数进行二阶展开近似，即将在处使用Taylor公式进行展开，保留至第三项

其中为在点处函数的一阶偏导向量，则为二阶偏导矩阵，即Hessian矩阵。对此近似表达式求梯度，并令其为0，得到

若矩阵可逆，则有

2.4 几何解释

函数过点的等值面为

我们在点处用一个与该等值曲面相切的二次曲面来进行近似表示，即为二阶近似展开式。且与梯度方向相互垂直。

3 具体算法

3.1 算法步骤

3.2 优缺点分析

1. 可以在理论上证明，Newton算法具有二阶收敛性（局部，即在最优点附近）；

2. 需计算f(x)的二阶导数（对复杂函数不容易）；

3. 对正定二次函数，迭代一次即可得到极小点。

3.3 code

TODO

4 改进的Newton法

TODO