神经网络西瓜书学习笔记：（第五章）

1943 年， [McCulloch and Pitts, 1943] 将上述情形抽象为图5.1所示的简单模型，这就是一直沿用至今 的 “M-P 神经元模型 “ 在这个模型 中 ， 神经元接收到来自 η 个其他神经元传递过来的输入信号.这些输入信号通过带权重的连接( connection) 进行传递，神经元接收到的总输入值将与神经元的阀值进行比较，然后通过”激活函数” (activation function) 处理以产生神经元的输出.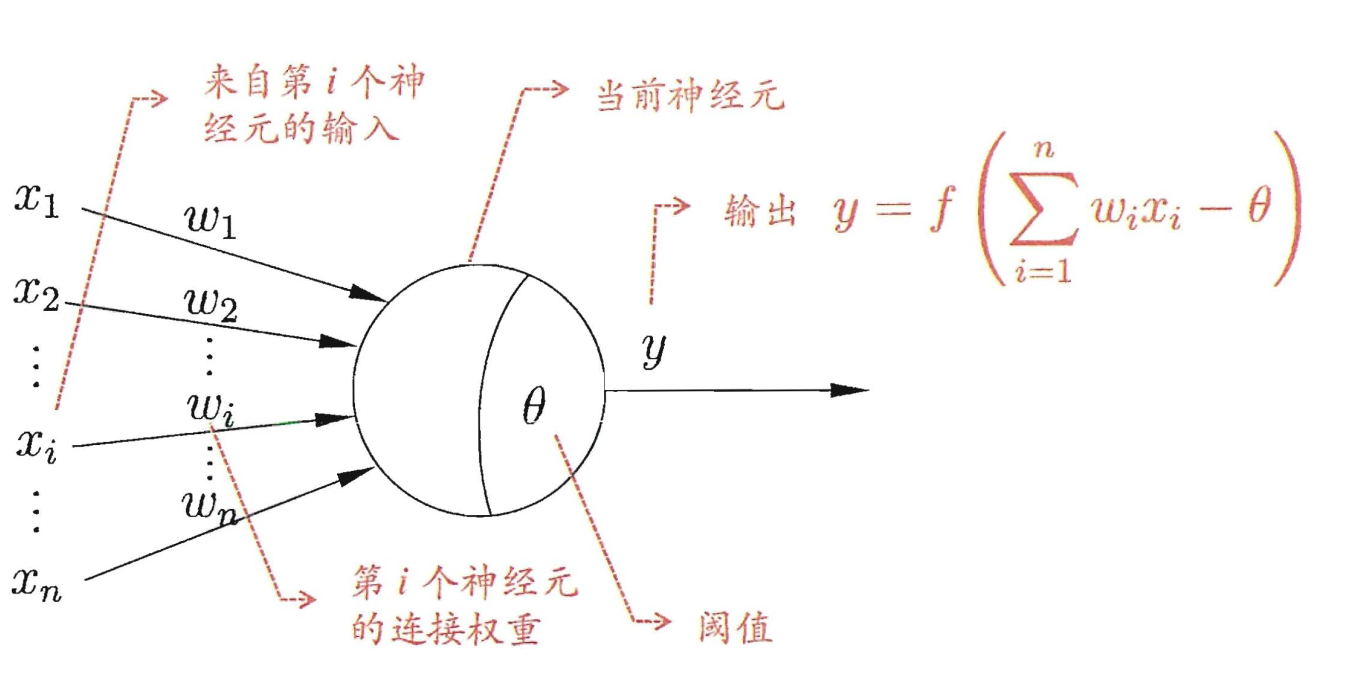
image.png
（神经元模型）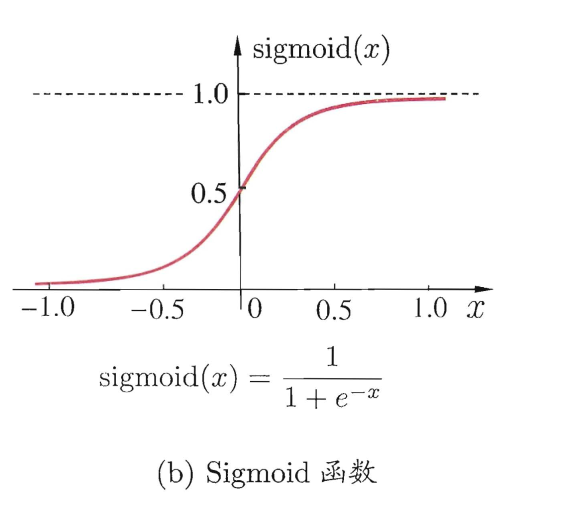
image.png
（通常的激活函数）

单层（感知机）：

必定解决线性可分问题，但是就算连异或都不能解决。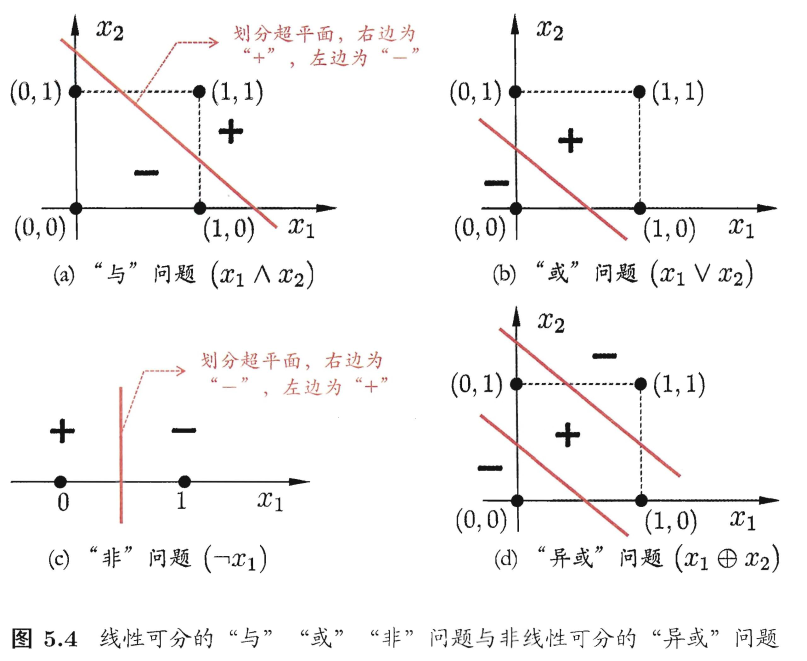
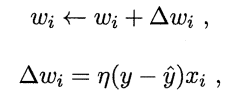
image.png
image.png
(调整公式）

多层：

神经网络学到的东西蕴含在链接权与阈值中。

误差逆传播算法：（BP）

推导过程详见西瓜书P102.这里记下了结论：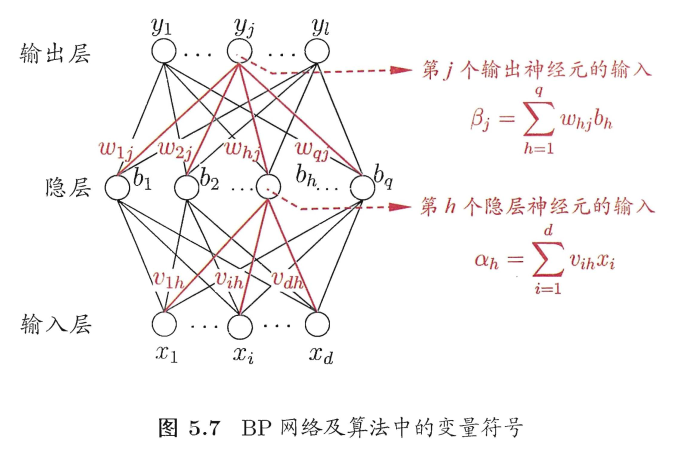
image.png
最终获得的结论：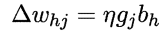
image.png
其中η是学习率，g下文截图有解释：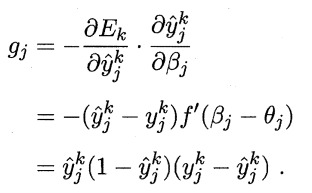
image.png
f为sigmoid函数，y带上标的那个是结果，不带上标的是真实标签。

全局最小与局部最小：

若用 E 表示神经网络在训练集上的误差，则它显然是关于连接权w和阈值θ的函数.此时，神经网络的训练过程可看作一个参数寻优过程，即在参数空间中，寻找一组最优参数使得 E 最小.
在寻找全局最小误差最小时我们通常会有以下3种方法：

  • 以多组不同参数值初始化多个神经网络，按标准方法训练后，取其中误差最小的解作为最终参数.这相当于从多个不同的初始点开始搜索，这样就可能陷入不同的局部极小从中进行选择有可能获得更接近全局最小的结果.
  • 使用 “模拟退火” (simulated annealing) 技术 [Aarts and Korst, 1989]. 模拟退火在每一步都 以二定的概率接受 比当前解更差的结果，从而有助于”跳出”局部极小. 在每步迭代过程中，接受”次优解”的概率要随着时间的推移而逐渐降低，从而保证算法稳定.
  • 随机梯度下降

上述方法均为启发式，没有理论的证明作为保障。
（更新于10：22）