线性回归

损失函数**：在模型训练中，我们需要衡量价格预测值与真实值之间的误差。通常我们会选取一个非负数作为误差，且数值越小表示误差越小。一个常用的选择是平方函数。 它在评估索引为 i 的样本误差的表达式为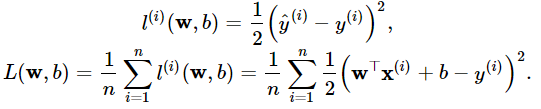

从零开始
1.生成/准备数据集
2.读取数据集
3.初始化模型参数
4.正态分布初始化：np.random.normal(loc(均值),scale(标准差),size(输出形状))
5.全零初始化：np.zeros()
6.定义模型

• torch.mm(矩阵相乘）
• torch.mul(点乘）

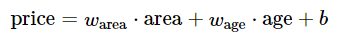
def linreg(X, w, b):
    return torch.mm(X, w) + b

7.定义损失函数
8.定义优化函数
9.小批量随机梯度下降，参数-学习率*梯度/batch_size
10.训练
11.前向传播
12.求损失
13.反向传播
14.优化参数
15.梯度清零

PyTorch中view的用法

把原先tensor中的数据按照行优先的顺序排成一个一维的数据（这里应该是因为要求地址是连续存储的），然后按照参数组合成其他维度的tensor。比如说是不管你原先的数据是[[[1,2,3],[4,5,6]]]还是[1,2,3,4,5,6]，因为它们排成一维向量都是6个元素，所以只要view后面的参数一致，得到的结果都是一样的。比如，

a=torch.Tensor([[[1,2,3],[4,5,6]]])
b=torch.Tensor([1,2,3,4,5,6])
print(a.view(1,6))
print(b.view(1,6))

得到的结果都是tensor([[1., 2., 3., 4., 5., 6.]])

再看一个例子：

a=torch.Tensor([[[1,2,3],[4,5,6]]])
print(a.view(3,2))

a=torch.Tensor([[[1,2,3],[4,5,6]]])
print(a.view(3,2))

将会得到：

tensor([[1., 2.],
       [3., 4.],
       [5., 6.]])

相当于就是从1，2，3，4，5，6顺序的拿数组来填充需要的形状。但是如果您想得到如下的结果：

tensor([[1., 4.],
        [2., 5.],
        [3., 6.]])

就需要使用另一个函数了：permute() 。PyTorch中permute的用法