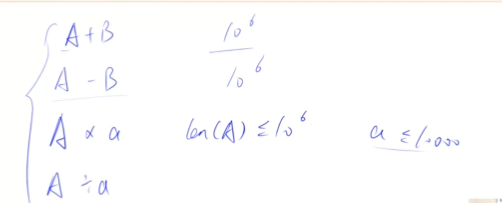高精度

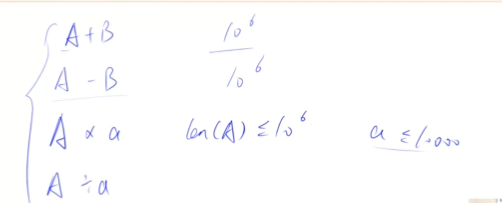
image.png
常用四种，注意数据范围。

高精度加法

  1. vector<int> add(vector<int> &A, vector<int> &B)
  2. {
  3.     if (A.size() < B.size()) return add(B, A);
  5.     vector<int> C;
  6.     int t = 0;
  7.     for (int i = 0; i < A.size(); i ++ )
  8.     {
  9.         t += A[i];
  10.         if (i < B.size()) t += B[i];
  11.         C.push_back(t % 10);
  12.         t /= 10;
  13.     }
  15.     if (t) C.push_back(t);
  16.     return C;
  17. }

Tips

  • 注意将输入转化为数字，再计算。
  • 注意使用 if (A.size() < B.size()) return add(B, A);简化比较过程。
  • 从个位开始存储，便于最高位进位。

高精度减法

  1. bool cmp(vector<int> &A, vector<int> &B){
  2.     if(A.size() != B.size()) return A.size() > B.size();
  3.     for(int i = A.size() - 1; i >= 0; i--){
  4.         if(A[i] != B[i])
  5.             return A[i] > B[i];
  6.     }
  7.     return true;
  8. }
  10. vector<int> sub(vector<int> &A, vector<int> &B){
  11.     vector<int> C;
  12.     for(int i = 0, t = 0; i < A.size(); i++){
  13.         t = A[i] - t;
  14.         if(i < B.size()) t -= B[i];
  15.         C.push_back((t + 10) % 10);
  16.         if(t < 0) t = 1;
  17.         else t = 0;
  18.     }
  19.     while(C.size() > 1 && C.back() == 0) C.pop_back();
  20.     return C;
  21. }
  23. int main(){
  24.     string a, b;
  25.     cin >> a >> b;
  27.     for(int i = a.size() - 1; i >= 0; i--)
  28.         A.push_back(a[i] - '0');
  29.     for(int i = b.size() - 1; i >= 0; i--)
  30.         B.push_back(b[i] - '0');
  31.     vector<int> C;
  33.     if(cmp(A, B)) C = sub(A, B);
  34.     else {
  35.         C = sub(B, A);
  36.         cout << '-';
  37.     }
  38.     for(int i = C.size() - 1; i >= 0; i--)
  39.         cout << C[i];
  40.     cout << endl;
  41.     return 0;
  42. }

Tips:

  • 当B大于A的时候，容易漏掉符号。比较放在sub函数内部不方便，因此抽离出cmp函数。
  • sub函数内部由于t表示的是当前位是否有借位，因此有t = A[i] - t;
  • 注意去除前导零。

**

高精度乘法

#include <iostream>
#include <cstring>
#include <vector>


using namespace std;

const int N = 100010;

vector<int> A;
int b;

vector<int> mul(vector<int> A, int b){
    vector<int> C;
    for(int i = 0, t = 0; i < A.size() || t; i++){
        if(i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t = t / 10;
    }

    while(C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

int main(){
    string a;
    cin >> a >> b;
    for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');

    auto C = mul(A, b);

    for(int i = C.size() - 1; i >= 0; i--)
        cout << C[i];
    return 0;
}

Tips

  • 与高精度减法相同，同样需要注意处理前导零！！！
  • 不要忘记引入vector头文件！！！
  • 思路值得借鉴，这里的进位可以不是像加法一样进位1，也不是像减法一样借位，而是可能是一个十位数，百位数….，不过不影响具体的流程，从低位到高位计算。
  • 最后一次进位的值可能很大，可以放入循环中，一起处理。也可以使用while循环处理进位t（但高精度加法由于最多进位是1，因此可以单独处理t）

高精度除法

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 100010;

vector<int> A;
int r;

vector<int> div(vector<int> A, int b, int& r){
    vector<int> C;
    int t = 0;
    for(int i = A.size() - 1; i >= 0; i--){
        t = t * 10 + A[i];
        C.push_back(t / b);
        t %= b;
    }   
    reverse(C.begin(), C.end());
    while(C.size() > 1 && C.back() == 0) C.pop_back();
    r = t;
    return C;
}

int main(){
    int b;
    string a;
    cin >> a >> b;
    for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');

    auto C = div(A, b, r);

    for(int i = C.size() - 1; i >= 0; i--) cout << C[i];

    cout << endl << r << endl;

    return 0;
}

Tips

  • 注意高精度除法，先计算的是高位，而前面几种优先算低位，因此最后结果还需要reverse一遍。
  • 不要忘记去除前导零！！！