前缀和
- 前缀和数组从1开始,s[0]定义成0。
- 作用:可快速算出一段区间的和
- 为什么需要s[0[, 是为了统一求所有区间的和,都使用s[j] - s[i - 1]这个公式。、
差分
- 差分是前缀和逆运算
- 差分数组就是原数组的差分,差分数组求前缀和得到原数组。
- O(n)时间得到前缀和数组。
- 作用:原数组l到r之间所有的值都加c,差分操作b[l] + c, b[r + 1] - c;使用O(1)的时间等效到将原数组l到r之间所有的值都加上c。差分数组是用来简化中间操作的,最终原数组通过对差分数组求前缀和得到。
-
IncDec序列问题

- 要使得整个数列的值相同,构造差分数组,即让b2到bn都为0
- 优先选择操作1,使得b2~bn中正值减1,负值加1,再选择操作2,3。
- 总操作次数就是,b2~bn中负数个数和正数个数中, 较多的那个。
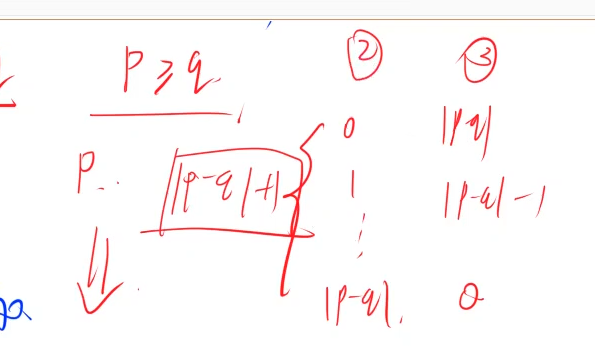
由于2,3操作都是可加可减,而b1的值代表了最终数量的值。
分配给2操作的个数不同,b1不同,则最终结果就不同,而分配给2,3的方案有|p - q| + 1种。
二维差分
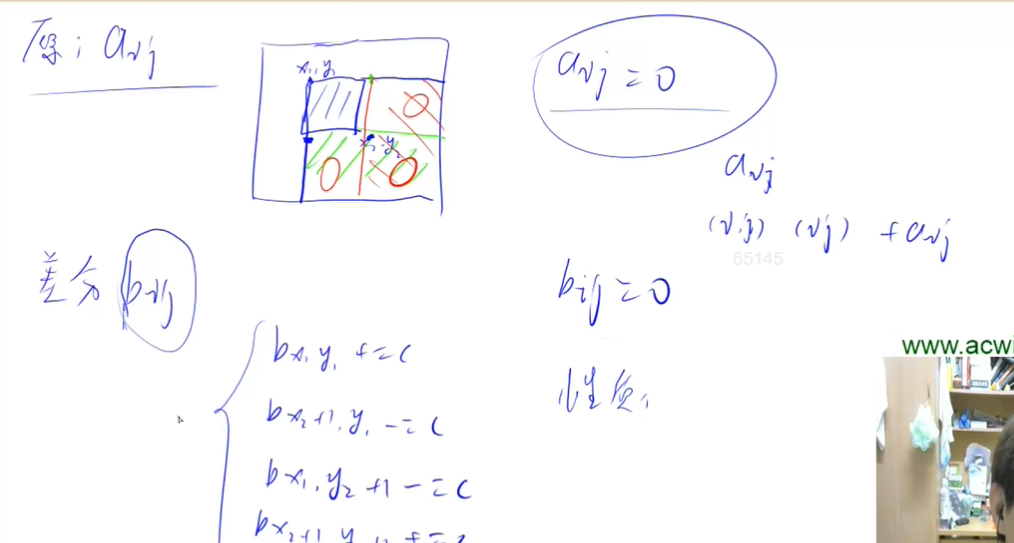
- 二维差分的正确理解应该是:
我们设法构造一个差分数组b[i,j],使得a[i,j]是b[i,j]的二维前缀和数组。
满足这个性质的b[i,j],应该是用来表示以i,j为左上顶点的矩形统一进行的加法操作。
假设构造好了b[i,j],然后再正着求a[i,j],就是二位前缀和的操作了。
位运算
lowbit(x)
返回x的最后一位1,对应的二进制数。
return x & -x;
- 因为-x 等于 ~x + 1, 所以使用 x & -x可以得到最后一位.
统计x的位数
反复用x - lowbit(x)直到x为0。
快速幂问题
使用O(logk)的时间复杂度 求出a的k次方 mod p的结果
- 把次数k用2的进制转换表示
- 预处理出所有a^2的x次方的数 mod p
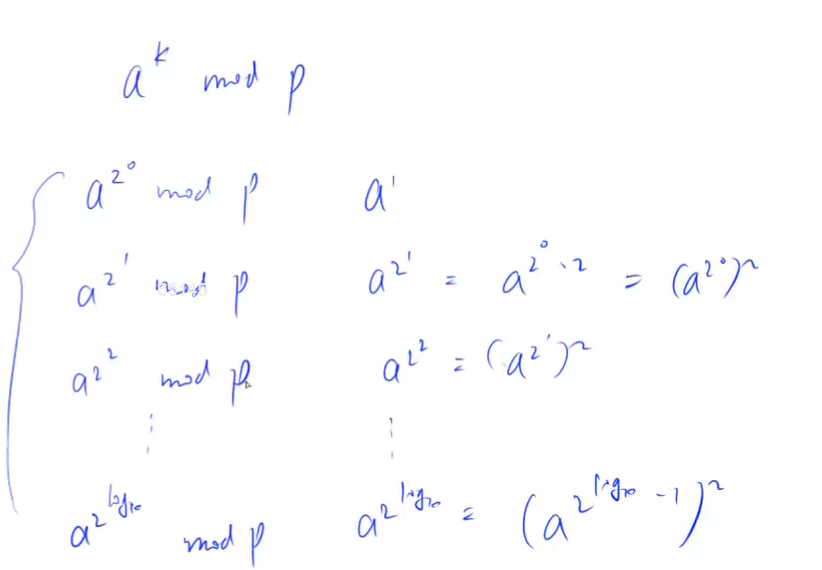
- 将k所有进制位为1对应的位的预处理出的值相乘再取。

