Chapter2 反向传播算法（BP）

反向传播算法（Back Propagation）是一种用于快速计算梯度的算法，其核心是一个对代价函数关于任何权重或偏置偏导数的表达式。该表达式告诉我们在该变权重和偏置时，代价函数变化的快慢，它可以帮助我们理解如何通过该变权重和偏置来改变整个网络的行为。

激活值之间的关系

为了计算代价函数对不同参数的偏导，我们需要得到各层激活值之间的关系，规定以下符号：

• ：第层第个神经元与第层第个神经元连接上的权重
• ：第层第个神经元的偏置

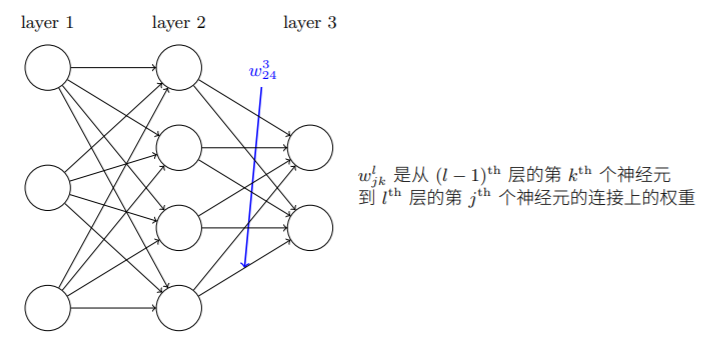
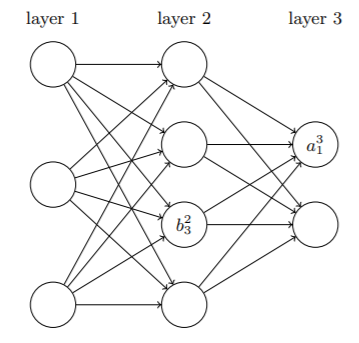
第层激活值与第层激活值之间的关系如下：

对其进行向量化，简化表达式得到：

为了后续记录的方便，记，称其为层神经元的带权输入，因此，方程亦可写作。

代价函数的两个假设

代价函数的基本形式：

其中，为训练样本总数；求和运算遍历所有训练样本；为对应的目标输出；表示网络的层数；是当输入为时网络输出的激活值向量。
为了让反向传播可行，需要对代价函数作两个假设：

1. 代价函数可以被写成在每个训练样本上的代价函数的均值。该假设是因为反向传播实质是对每个独立的样本计算偏导数，然后再在所有训练样本上平均化得到代价函数对参数的偏导。

2. 代价可以写成神经网络输出的函数。即：代价函数是的函数。

   Hadamard乘积

   即向量按元素的乘积运算，是反向传播算法的基本运算之一
   

   反向传播的四个基本方程

   首先定义一个中间量，作为神经元误差的度量：
   
   当每次施加很小的变化在上时，各神经元的输出就会从变为，该误差向后传递，最终导致总代价发生的改变。因此每次只需选择与符号相反的，就可以使得网络输出得到有效的改善。此时，若足够小，则通过在上施加扰动对于整个网络的改善取得的效果已经很有限了，神经元已经接近最优了。
   反向传播正是提供一种计算每层的方法，然后将这些误差和最终我们需要的量 和 联系起来，以便神经网络的学习。

   四个基本方程

   所有方程的证明都是基于多元微积分求导的链式法则得到的。

   输出层误差的方程

   误差各元素定义如下：
   
   复合函数求导，运用了链式法则。
   右边两个部分都很好计算，前者依赖于代价函数形式，由于给定二次函数因此容易计算。
   其对应矩阵形式：
   

   各层误差间的反向传递方程

   「反向传播」名字的来源，通过前一方程得到输出层误差后，可以通过该方程反推任意层各神经元的误差：
   

   代价函数关于网络中任意偏置的改变率

   
   直观解释，对任一神经元，改变和是完全一致的。
   对应的矩阵形式简记为：
   

   代价函数关于任意权重的改变率

   
   同样的，对于任一权重而言，相比其导数无非是多乘了一个输出值
   该方程也可写作：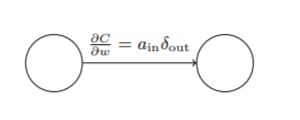
   
   

   神经元的饱和

   当 近似为 0 或者 1 的时候函数变得⾮常平（斜率很小）。这时 。所以如果输出神经元处于或者低激活值（≈ 0）或者⾼激活值（≈ 1） 时，最终层的权重学习缓慢。此时称该输出神经元已饱和，权重学习要么十分缓慢，要么直接终止。对于其他层也是如此，在方程2中，只要非常小，接近饱和，权重和偏置的学习就会变得缓慢。

   反向传播算法

   算法流程

   基于以上方程可以得到反向传播算法的具体实现步骤：

3. 输入：为输入层设置对应的激活值

4. 前向传播：对每个计算相应的带权输入和激活值
5. 得到输出层误差：利用基本方程一计算
6. 反向误差传播：对每个，利用基本方程二反向推算各层误差
7. 输出：代价函数的梯度由基本方程三、四得到

反向传播算法中的「反向传播」正是体现在误差在各层网络间一层层的反向传导，在计算出输出层误差后，需要在前一层寻找输出层误差来源，借助链式法则进而不断回退至第一层。

反向传播算法+随机梯度下降

在反向传播算法计算出的梯度基础上，结合随机梯度下降就可以实现网络的训练，完善后的学习算法如下：

1. 输入训练样本的集合
2. 对每个训练样本：设置对应的输入激活
   • 前向传播
   • 输出误差
   • 反向误差传播

梯度下降：对每个，根据 和 更新权重和偏置。
其中，对于每一小批次样本中的每个样本要建立一个循环，各批的梯度下降也要建立一个循环。

代码实现

主要是反向传播算法的实现部分：
（x,y,weights等变量的数据类型均为numpy.array）

def backprop(self, x, y):
    nabla_b = [np.zeros(b.shape) for b in self.biases]
    nabla_w = [np.zeros(w.shape) for w in self.weights]
    # 前向传播
    activation = x
    activations = [x]  # 按层存储激活值，每个元素代表一层的激活值
    zs = []  # 存储各层的加权输入z
    for b, w in zip(self.biases, self.weights):
        z = np.dot(w, activation)
        zs.append(z)
        activation = sigmoid(z)
        activations.append(activation)
    # 反向传播
    delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(zs[-1])  # 利用cost_derivative函数计算对输出层激活值的偏导，再计算输出层的偏差
    nabla_b[-1] = delta
    nabla_w[-1] = np.dot(delta, activation[-2].transpose())  # transpose()转置函数、
    # 下方的l与书内l不同，利用了python负数索引的优势
    for l in range(2, self.num_layers):
        z = zs[-l]
        sp = sigmoid_prime(z)
        delta = np.dot(self.weights[-l+1].transpose(), delta)*sp
        nabla_b[-l] = delta
        nabla_w[-l] = np.dot(delta, activation[-l-1].transpose())
    return (nabla_b, nabla_w)

补充：python中的*、np.dot和np.multiply辨析 对于array来说，* 和 dot()运算不同：

• *是每个元素对应相乘
• dot()是矩阵乘法

对于matrix来说，* 和 multiply() 运算不同：

• *是矩阵乘法
• multiply() 是每个元素对应相乘

习题中提到可以更改为矩阵形式运算同时对批内的所有样本计算梯度，全矩阵形式的具体实现如下：

def backprop(self, mini_batch):
    # mini_batch为一个列表，其元素为输入值x与期望输出值y组成的二维元组
    # x,y均为numpy.array类型变量

    # 首先应构造包含所有样本的输入矩阵X与期望输出矩阵Y
    # X = [x for x, y in mini_batch]

相比其他计算梯度的方法，反向传播算法的计算代价约为前向传播的两倍，它同时计算了所有的偏导数，效率较高。

全局观

从直觉来看，反向传播算法借助追踪一个的微小变化如何导致代价函数值的改变的表达式来计算对应的偏导数。

你可以将反向传播想象成⼀种计算所有可能的路径变化率的求和的⽅式。或者，换句话说，反向传播就是⼀种巧妙地追踪权重（和偏置）微⼩变化的传播，抵达输出层影响代价函数的技术。

假设我们对一些网络中的做一点小小的变动，这个改变会导致在其对应神经元输出激活值上的相应改变。紧接着，引发链式效应，对下一层所有激活值产生影响，这些改变将会影响到一个个下一层，到达输出层，最终影响代价函数。

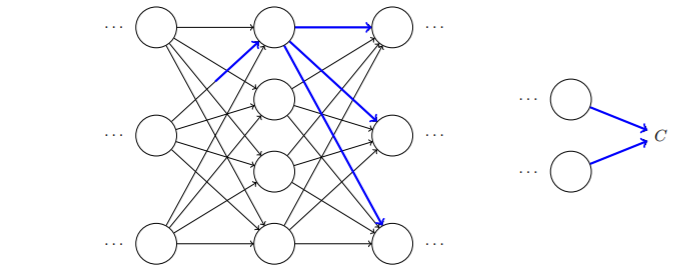
所以代价函数改变和就按照下面的公式关联：

将该变化反映在公式上，导致了神经元的激活值的变化：

的变化将会导致下一层所有激活值的变化：

代入方程得到：

所以，对于其中一条可能的变动传播路径，有

对所有传播路径产生的变化量求和，得到代价函数值总体变化量：

所以