矩阵 - 空间变换的数值描述

学习图形可视化之前：学数学有什么用？我不学。

开始学图形可视化之后：这是什么数学公式？怎么这么多符号？

为了让学习能顺利进行下去，我不得不去补一下线性代数的知识，如果你和我一样对图形可视化感兴趣，那就让我们一起开启这趟数学真香之旅。

说到图形变换，很多教程里面都会有矩阵这个概念，矩阵这个东西在学它的时候留给我的只是一堆数值的计算，绝对没想到它和空间变换有什么关系。那我们就从最最基础的知识向量开始，来一步一步了解矩阵在空间变换中所描述的内容。

为了不把事情搞的太复杂，以下的概念都在二维空间中讨论。

向量

在物理学和工程学中，几何向量更常被称为矢量。许多物理量都是矢量，比如一个物体的位移，球撞向墙而对其施加的力等等。与之相对的是标量，即只有大小而没有方向的量。一些与向量有关的定义亦与物理概念有密切的联系，例如向量势对应于物理中的势能。

在数学中，向量，指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。

在图形世界里，向量是空间中的箭头。为了让向量有一个更具体的概念，我们建立一个坐标系，让这个向量落在坐标系中，向量的起点始终在坐标轴的原点。

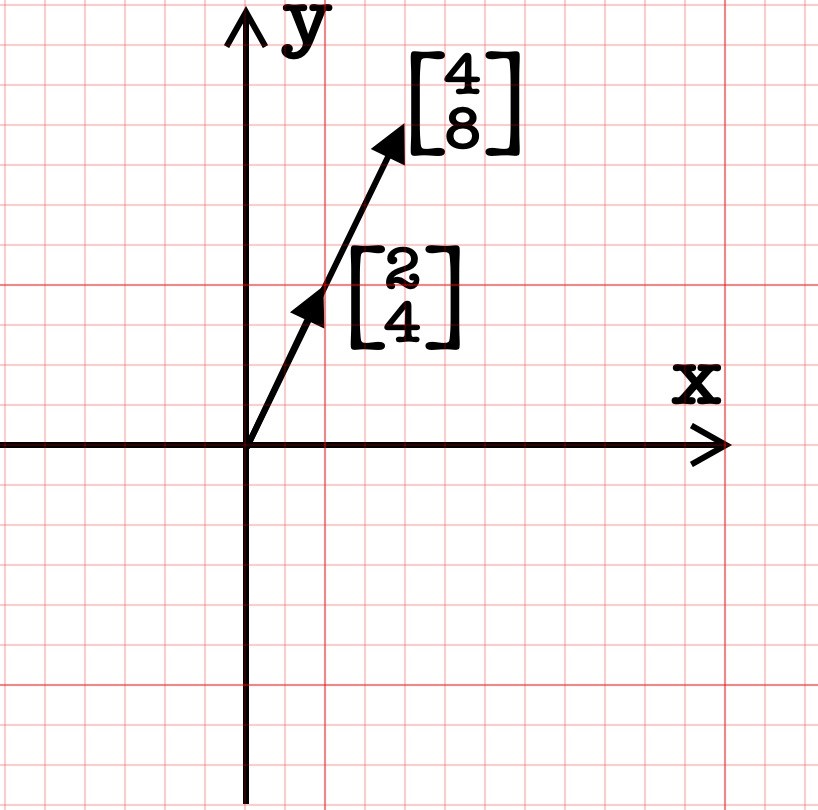
向量是有序的数字列表，所以我们可以通过向量坐标来理解它:

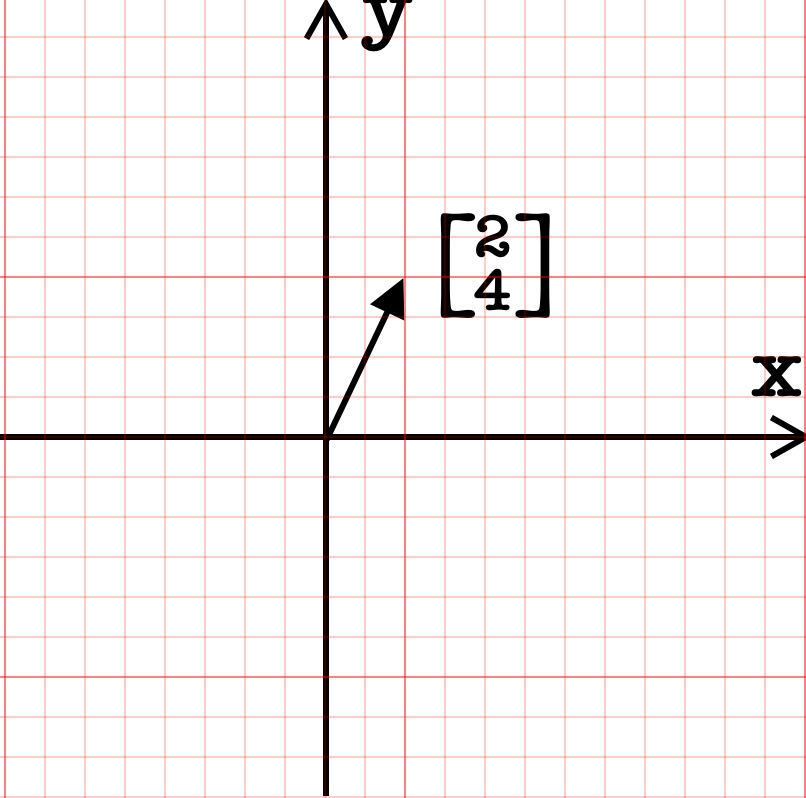
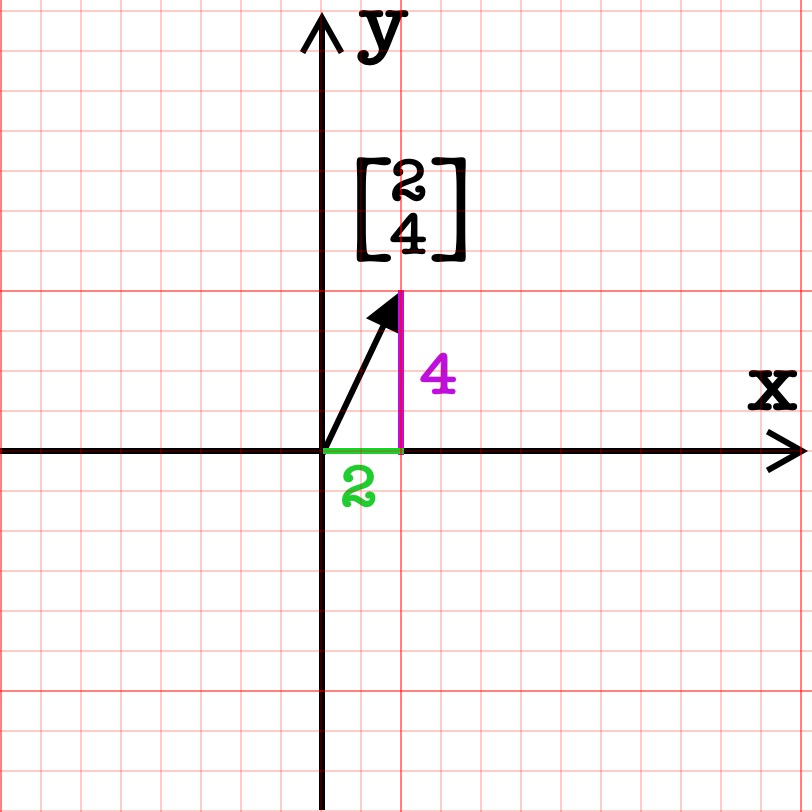
一个向量的坐标由一对数构成，这对数指导你如何从原点（向量起点）出发到达它的尖端（向量终点），我们先从 X 轴向正方移动 2 个单位，再延 Y 移动 4 个单位就得到了我们现在的坐标。

向量相加

假设我们有两个向量，需要计算它们相加的值： +

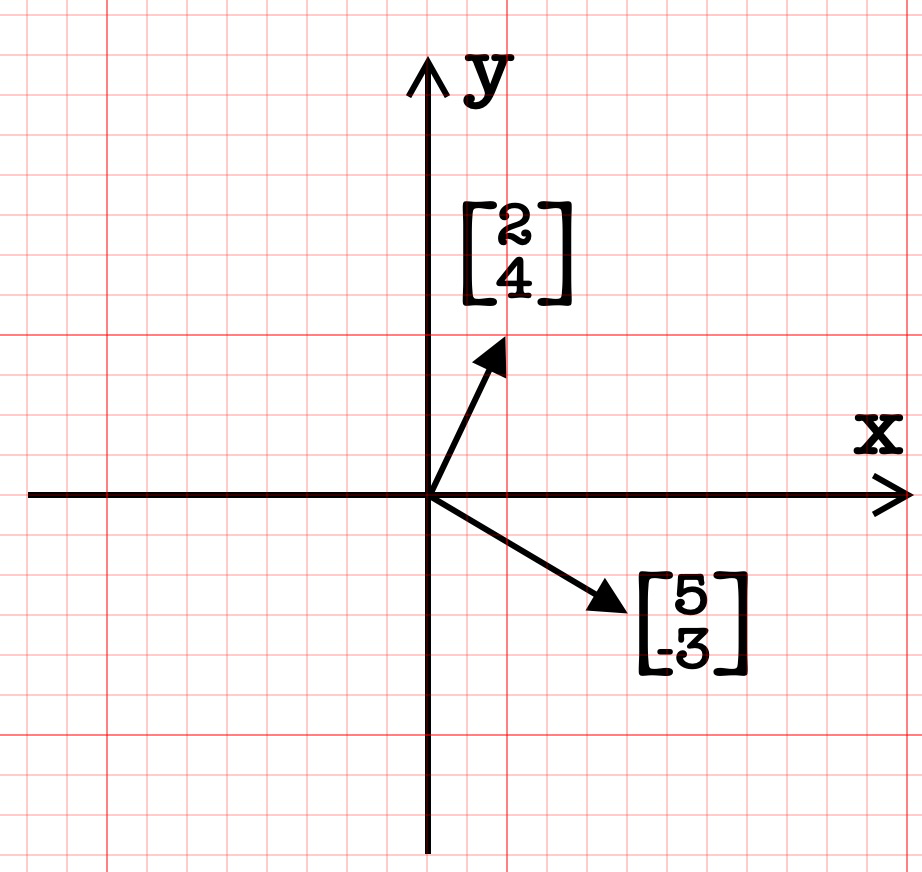
为了更直观的描述这两个向量相加，我们还是利用坐标系来看具体发生了什么，在向量那一部分里面我们通过在 x 轴和 y 轴来描述一个向量。向量相加时，我们把第一个向量的终点作为第二个向量的起点，再向x轴移动第二个向量x的移动距离，向 y 轴移动第二个向量的 y 轴距离，就得到了两个向量的和：

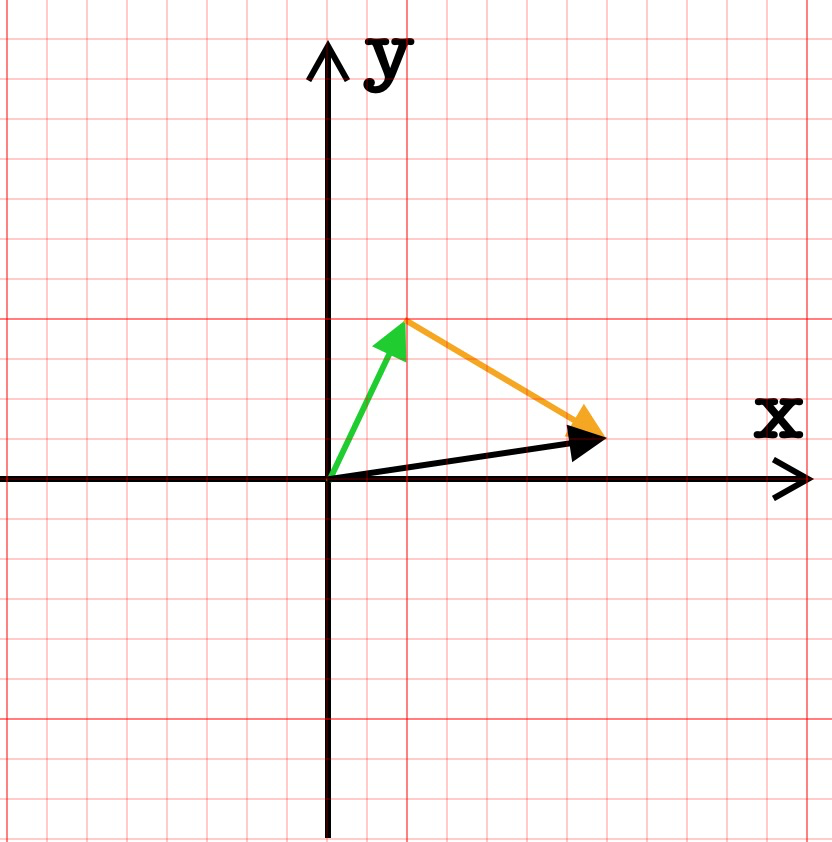
所以可以把向量看作一种特定的运动：即在空间中朝着一个方向迈出一定距离，如果你先沿着一个方向移动，接着再沿着另一个方向运动，结果和你沿着这两个方向的和运动是一样的：

+ = =

向量缩放

向量的缩放值称为标量，向量与标量相乘就是将向量中的每个分量与标量相乘：

2 * =

线性代数围绕两种基本运算：向量相加与向量相乘。

基向量

当你看到一对描述向量的数时，比如 ，你可以把它每个坐标看做一个标量，也就是说它们如果拉伸或者压缩了一个向量。在 xy 坐标系中，有两个非常特别的向量：一个指向正右方，长度为 1，通常被称为 或者 x 方向的单位向量；另一个指向正方向，长度为 1，通常被成为 或者 y 方向的单位向量。现在想象向量 的 x 坐标是一个标量，他将拉伸为原来的 2 倍，y 坐标也是一个标量，它将 拉伸为原来的 4 倍。从这个角度去看，这个向量实际上是两个经过缩放的向量的和：

2 + 4 =

和 是 xy 坐标系的 基向量。

每当我们用数字描述向量时，它都依赖我们正在使用的基。

如果我们选择不同的基向量会怎么样？

空间

两个向量标量乘法之和的结果被称为这两个向量的线性组合。

这个线性来自哪里呢？如果固定其中一个标量，让另一个标量自由变化，所产生的向量的终点会描出一条直线。如果你让两个标量同时自由变化，考虑所有可能得到的向量。大部分情况下，对于一切初始向量，你能到达平面的每一个点，所有二维向量都尽在掌握。

所有可以表示为给定向量线性组合的向量集合，被称为给定向量张成的空间。对大部分二维向量来说，它们张成的空间是所有二维向量的集合：

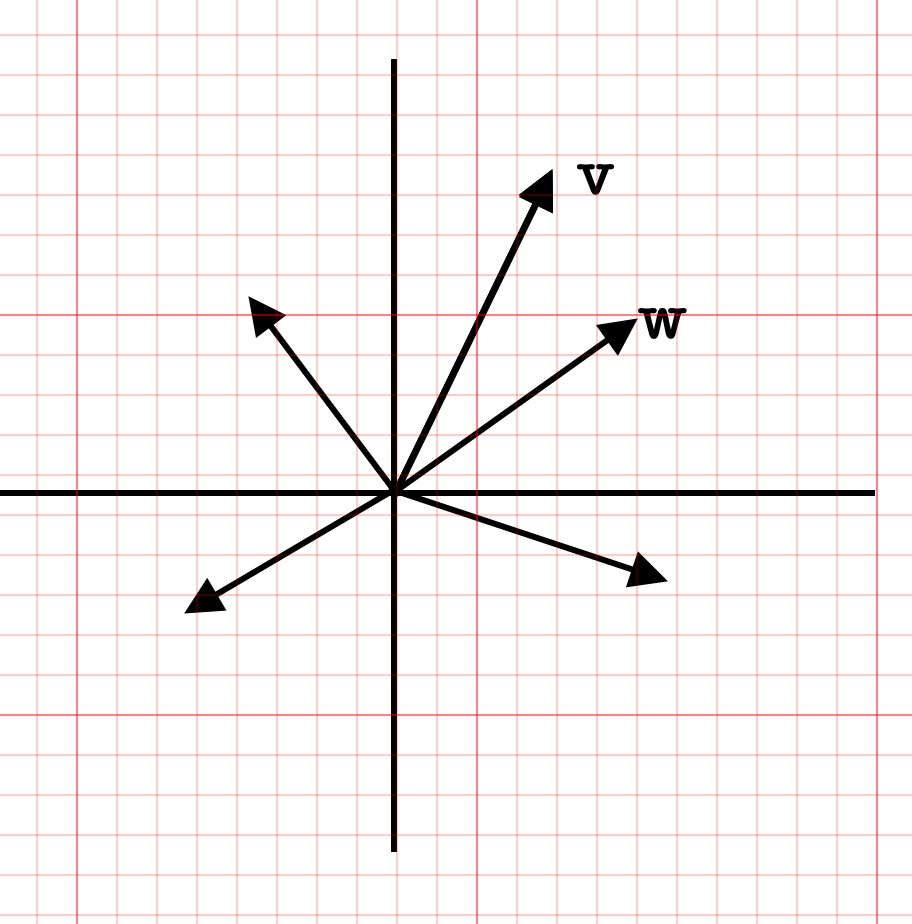
与 全部线性组合构成的向量集合称为 ”张成的空间“： ，a与b在实数范围内变动。

向量与点

如果你想象一条线上落满了向量，同时想象所有二维向量填满平面时，你会觉得非常拥挤。所以我们可以用向量的终点来代表该向量，但是它的起点仍然位于原点。所以你想象一条直线上的向量，你只需要想象一条直线，同样的，你考虑所有二维向量时，你把每个向量抽象为它的终点，实际上，你就不必考虑所有的箭头了，只需要考虑无限大的二维平面本身。

所以当你处理一个向量时，你可以把它看作一个箭头；当你处理一系列向量时，你可以把它们看作一系列点。

线性变换和矩阵的关系

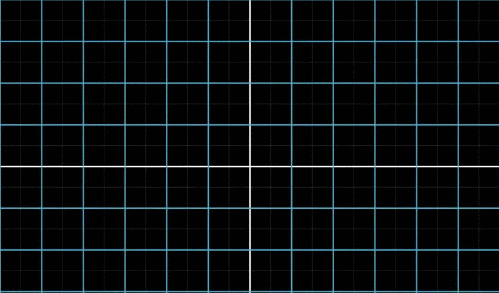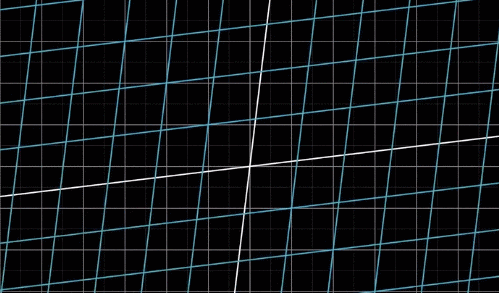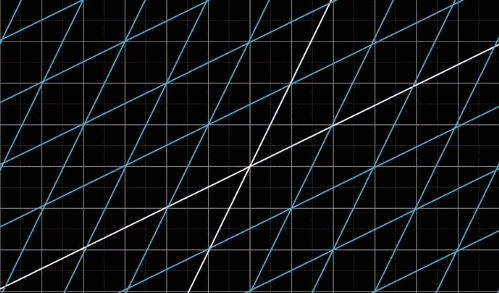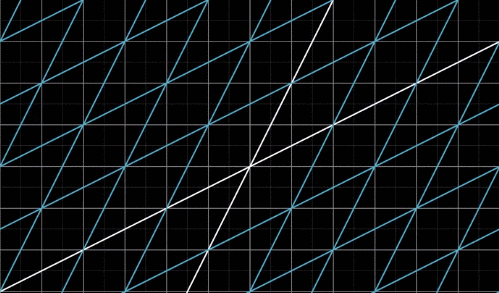
线性变换在空间到底长什么样呢，下面这张图会给你一个直观的感受：

变换实际上是一个函数的花哨说法：

fn * =

变换这个词在暗示你用运动去思考：如果一个变换接收一个向量并输出一个向量。我们想象这个输入向量移动到输出向量的位置。接下来，要理解整个变换，我们可以想象每一个输入向量都移动到到对应的输出位置，如果把每个向量看作是一个点，我们可以想象空间中的所有点移动到其他点的位置。各种各样的变换所产生的效果是很美妙的。任意一个变换也可以非常复杂的。现在我们要讨论的变换就限制在一种特殊类型上的变换：线性变换。

直观地说，如果一个变换具有以下两条性质，我们就称它是线性的。一是直线在变换后仍然保持为直线，不能有所弯曲，二是原点必须保持固定。总的来说，你应该把线性变换看作是：保持网格线平行并等距分布的变换。

如何用数值描述线性变换呢？

实际结果是，你只需要记录两个基向量，也就是 和 变换后的位置，其他向量都会随之而动。假设我们有一个向量 为即 = -1 + 2 ；如果我们运动一些变换，那么变换后的向量 也是变换后 和 的线性组合：

Tansformed = -1(Tansformed ) + 2(Tansformed )

这就意味着，你可以只根据 和 的落点，来推断出 的落点。假设我们变换后 的落点为， 的落点为那么变换后的 则为： =

这个时候可以停下来想一下，这个其实是一个空间变换的过程。所以空间中的所有点都发生了变换：

=> x + y =

一个二维线性变换仅有四个数字就完全确定了。通常我们将这些坐标包装在一个 2 2 的格子里，称它为 2 2 的矩阵： ，其中就是变换后 的落点，就是变换后 的落点。如果你想知道任何一个向量经过这样的变换后的值，你只需要取出向量的坐标，将它们分布与矩阵的特定列相乘，然后将结果相加即可。

= 5 + 7

所以我们可以得出我们在上学时的公式

= x + y =

接下来我们练习用矩阵描述一些线性变换：比如我们将整个空间逆时针旋转 90 度

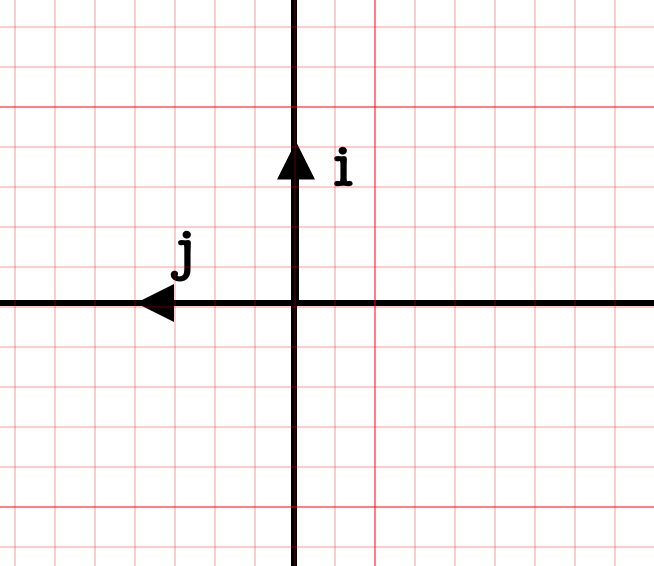
那么 的落点， 的落点为，则使用可以用来描述这一空间变换。

小结

我们来总结一下，我们用运动的思维来描述了向量，通过选择不同的基向量建立不同的空间，而矩阵正是描述一种空间到另一种空间变换的数值。

线性代数给计算机图形提供了一种语言，让我们通过计算机能处理的数字来描述并操纵空间。