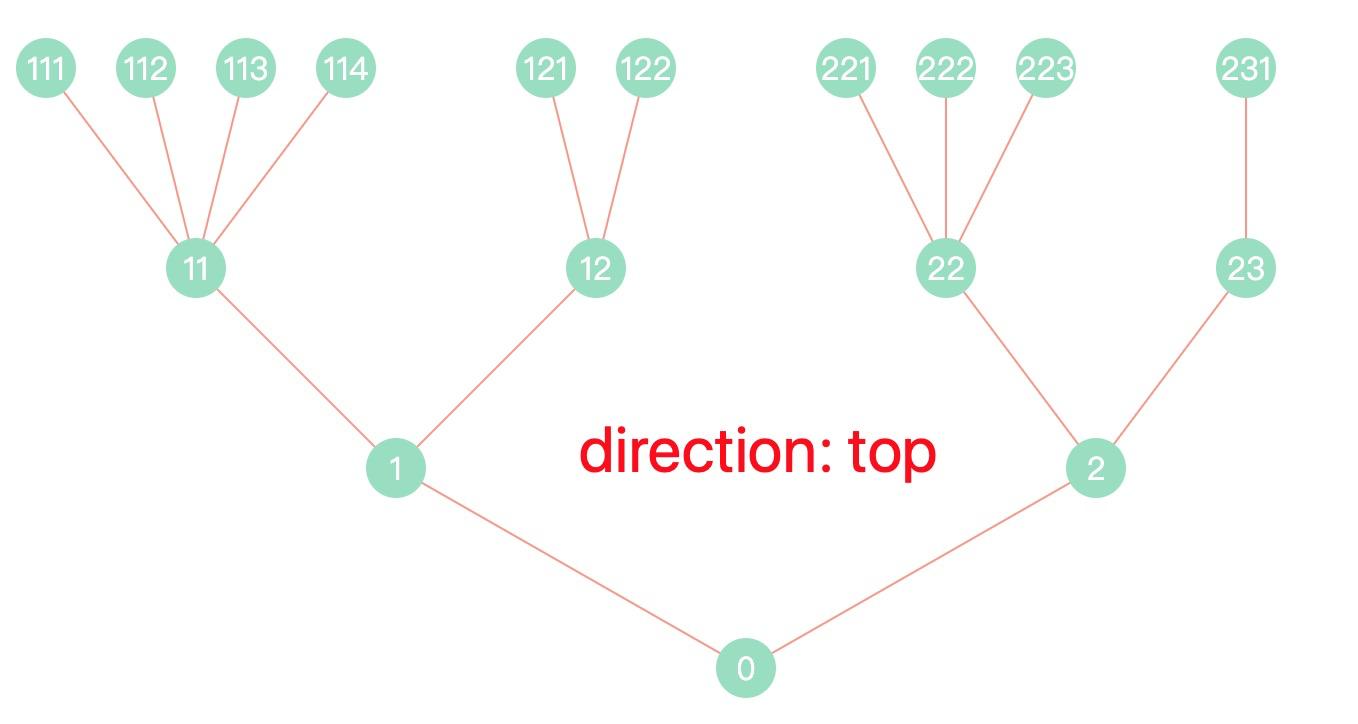
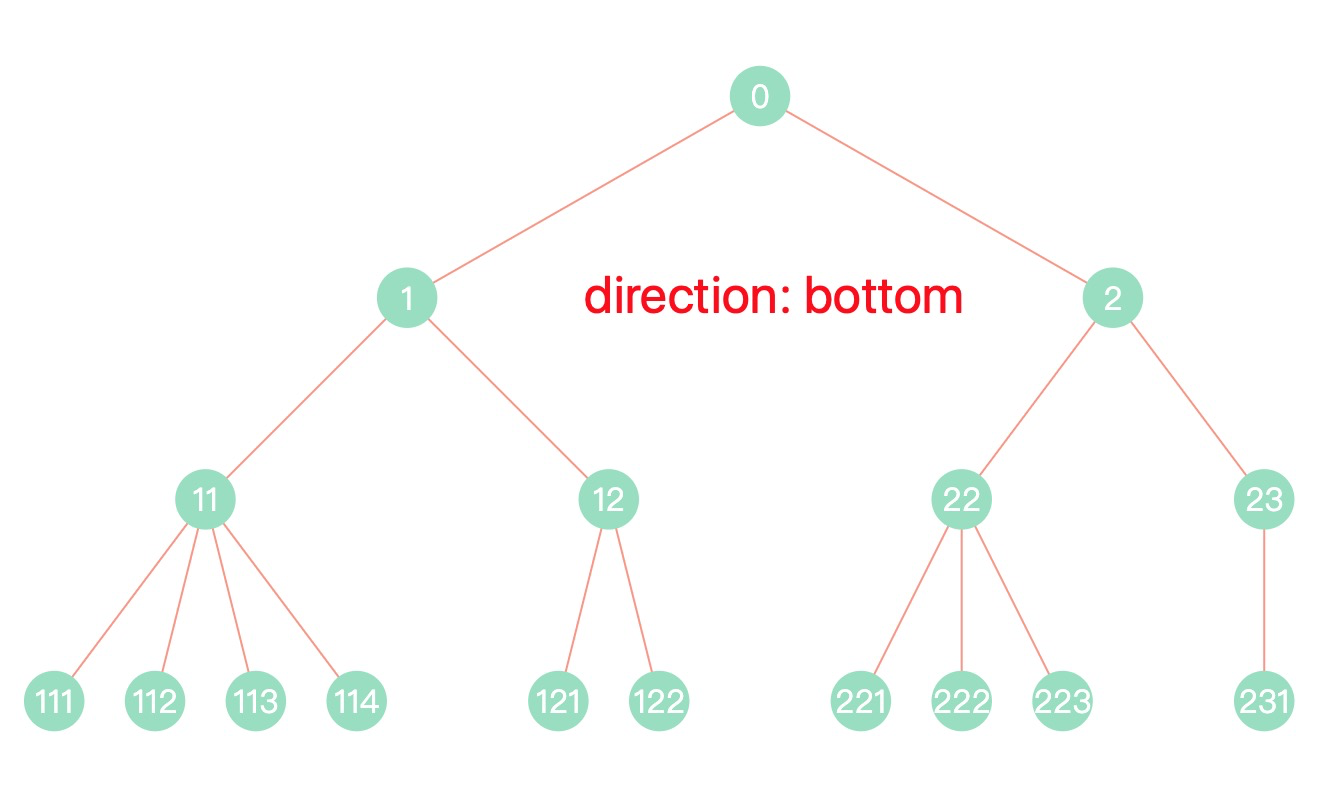
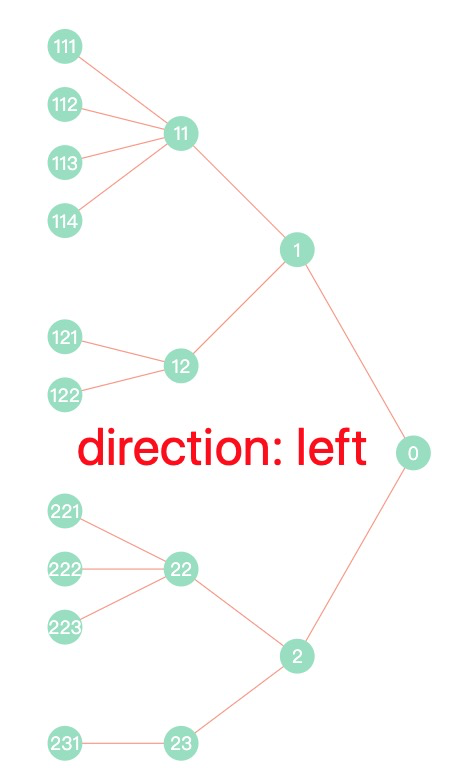
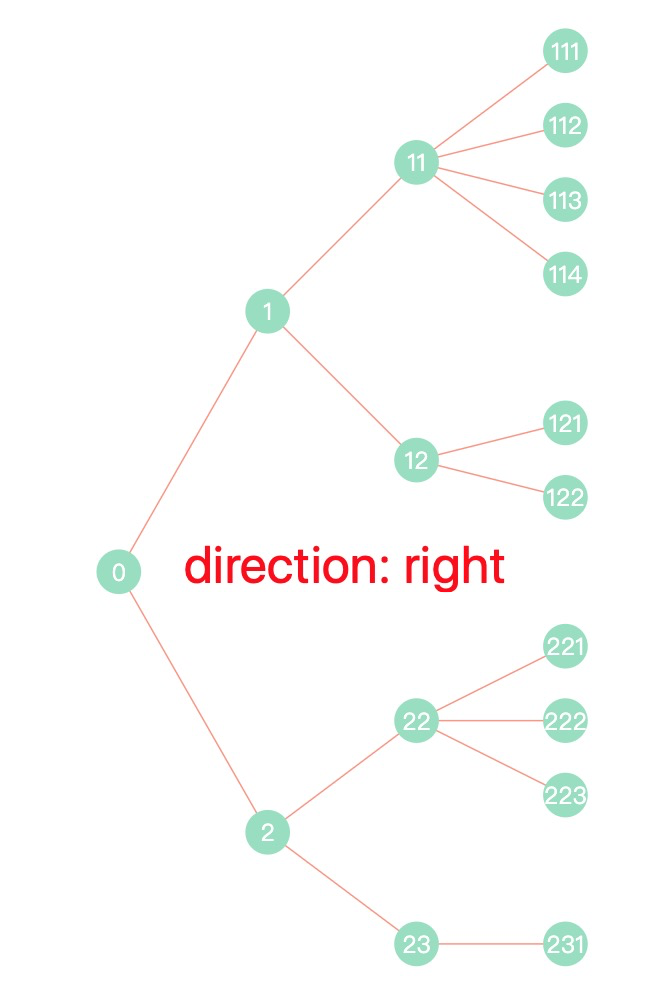
最近在做企业风控相关的产品，常常涉及企业上下游行业、企业关联关系等信息的展示，为了更好地表达这些关系，我们常常使用树形图来描述这些关系，如下图所示：

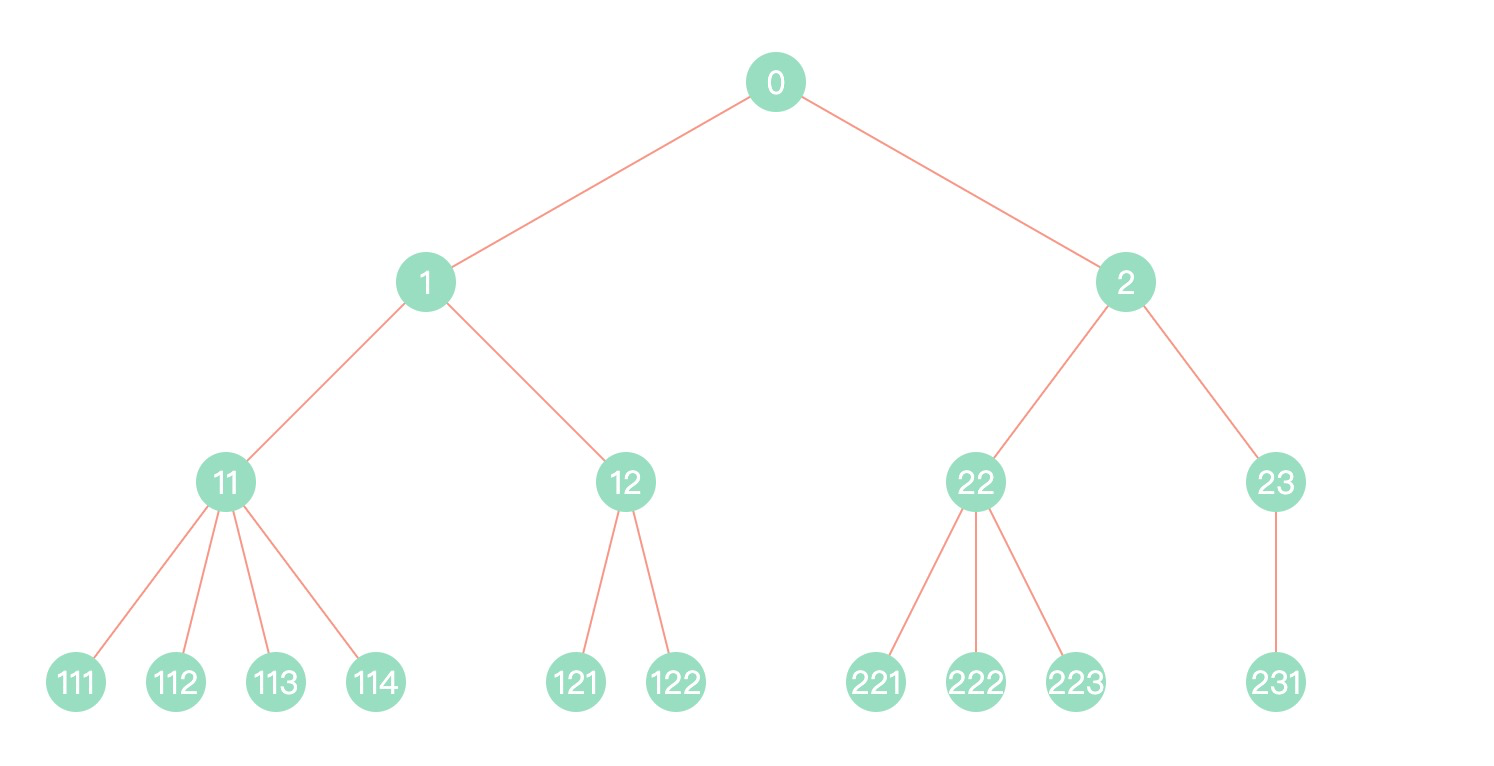
image.png
我们期望这个树形布局有以下特点：

  • 同一层级节点在同一水平线上；
  • 父节点位置始终在子节点中间位置；
  • 子节点不允许重叠；
  • 相邻节点有一定间距，且不同父节点的相邻节点加大间距区分。

传统的树形布局通常将子节点按照兄弟节点的最大宽度分开（一个节点的最大宽度即以该节点为根的树所占的最大宽度）。这样做虽然代码上容易实现，只要在每个节点保存该子树的最大宽度即可，但是视觉上不够美观，比较浪费空间。在某些传统布局甚至限制子节点的数目。

而这种布局与传统的树形布局有很大不同，它做到了在布局上节点与节点尽可能地紧凑，而且始终保持对称性和任意子节点数目。

实现我们期望的树形布局，最关键的一步是怎么从最底层一步步推导出全树节点的位置。

算法的实现步骤如下：

  1. 遍历树形结构数据，得出树形节点 id 和 节点的映射关系、以及一个二维数组保存了每一个层级的节点；
  2. 遍历二维数组：计算底层节点位置，向上修正父节点位置，得出节点数组；
  3. 遍历节点数组，计算出连接线数组，得出图形数据。

接下来我们就通过代码来具体实现：

第一步：数据准备

我们先准备一份树形结构数据：

  1. const treeNodes = [
  2.   {
  3.     id: '0',
  4.     name: '0',
  5.     children: [
  6.       {
  7.         id: '1',
  8.         name: '1',
  9.         children: [
  10.             {
  11.                 id: '11',
  12.                 name: '11',
  13.                 children: [
  14.                     {
  15.                         id: '111',
  16.                         name: '111'
  17.                        },
  18.                     {
  19.                         id: '112',
  20.                         name: '112'
  21.                        },
  22.                        {
  23.                         id: '113',
  24.                         name: '113'
  25.                        },
  26.                        {
  27.                         id: '114',
  28.                         name: '114'
  29.                        }
  30.                   ]
  31.              },
  32.             {
  33.                 id: '12',
  34.                 name: '12',
  35.                 children: [
  36.                   {
  37.                     id: '121',
  38.                     name: '121'
  39.                    },
  40.                    {
  41.                     id: '122',
  42.                     name: '122'
  43.                    },
  44.                 ]
  45.              }
  46.         ]
  47.       },
  48.       {
  49.         id: '2',
  50.         name: '2',
  51.         children: [
  52.             {
  53.                 id: '22',
  54.                 name: '22',
  55.                 children: [
  56.                   {
  57.                     id: '221',
  58.                     name: '221'
  59.                   },
  60.                   {
  61.                     id: '222',
  62.                     name: '222'
  63.                   },
  64.                   {
  65.                     id: '223',
  66.                     name: '223'
  67.                   },
  68.                 ]
  69.             },
  70.             {
  71.               id: '23',
  72.               name: '23',
  73.               children: [
  74.                 {
  75.                   id: '231',
  76.                   name: '231'
  77.                 }
  78.               ]
  79.           }
  80.         ]
  81.       }
  82.     ]
  83.   }
  84. ];

第二步：计算层级

定义节点数据类型

  1. interface INode {
  2.   id: string | number,
  3.   name: string | number,
  4.   children?: Array<INode>,
  5.   parentId?: string | number,
  6.   depth?:  number,
  7.   x?: number,
  8.   y?: number
  9. }

遍历数据，计算出节点二维数组，以及节点 hash 表，用于映射节点：

  1. export function iterator(treeNodes: Array<INode>, rootId = 'root'): {
  2.   matrix: Array<Array<INode>>,
  3.   hash: {}
  4. } | void {
  5.   if (!treeNodes || !treeNodes.length) return;
  7.   /**
  8.    * matrix [
  9.    *    0 [ node(0) ],
  10.    *    1 [ node(1), node(2), node(3) ],
  11.    *    2 [ node(11), node(12), node(13), node(21), node(22), node(23) ],
  12.    *    3 [ node(111), node(112), node(113), node(121), node(122), node(123), ... ]
  13.    * ]
  14.    */
  15.   let matrix: Array<Array<INode>> = [];
  17.   /**
  18.    * hash {
  19.    *    [node.id]: node
  20.    *    ...
  21.    * }
  22.    */
  23.   let hash = {};
  25.   let stack: Array<INode> = [];
  27.   // 第一层节点入栈
  28.   for (let i = 0, len = treeNodes.length; i < len; i++) {
  29.     // 增加属性
  30.     treeNodes[i].parentId = rootId;
  31.     treeNodes[i].depth = 0; // 从 0 开始
  33.     // 剔除 children 属性后存入 matrix
  34.     const { children, ...rest } = treeNodes[i];
  35.     matrix[0] = matrix[0] || [];
  36.     matrix[0].push({ ...rest });
  38.     // 保留 children 属性用于遍历
  39.     stack.push(treeNodes[i]);
  40.   }
  42.   let item;
  44.   while(stack.length) {
  46.     item = stack.shift(); // 出栈
  47.     hash[item.id] = item; // 存入 hash
  49.     if (item.children && item.children.length) {
  50.       item.children.forEach(child => {
  51.         // 增加属性
  52.         child.parentId = item.id;
  53.         child.depth = item.depth + 1;
  55.         // 剔除 children 属性后存入 matrix
  56.         const { children: _children, ...rest } = child;
  57.         matrix[child.depth] = matrix[child.depth] || [];
  58.         matrix[child.depth].push({ ...rest });
  59.       });
  61.       stack = item.children.concat(stack);
  62.     }
  63.   }
  65.   return {
  66.     hash,
  67.     matrix
  68.   };
  69. }

第三步：计算节点位置

主体函数结构如下：

  1. function getLayout(
  2.   origin: { x: number, y: number},
  3.   offset: { offsetDepth: number, offsetNode: number },
  4.   direction: 'top' | 'right' | 'bottom' | 'left' = 'right'
  5. ): {
  6.   nodes: Array<INode>,
  7.   links: Array<ILink>
  8. } {
  9.     // codes goes here
  10. }

参数说明：

  • origin: 图形坐标轴原点 (x, y), 如下图所示：

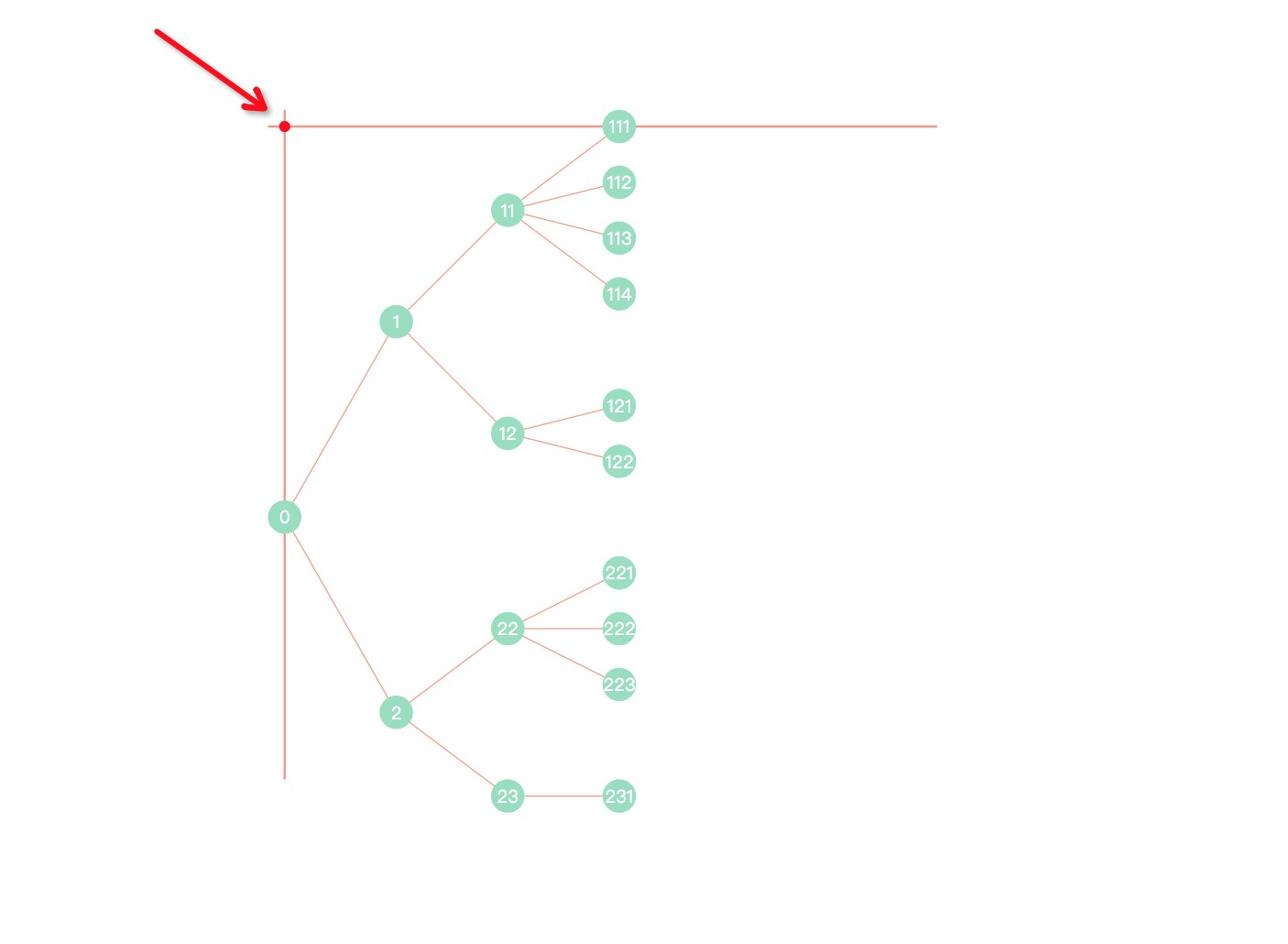
image.png

  • offset：层级和节点偏移量

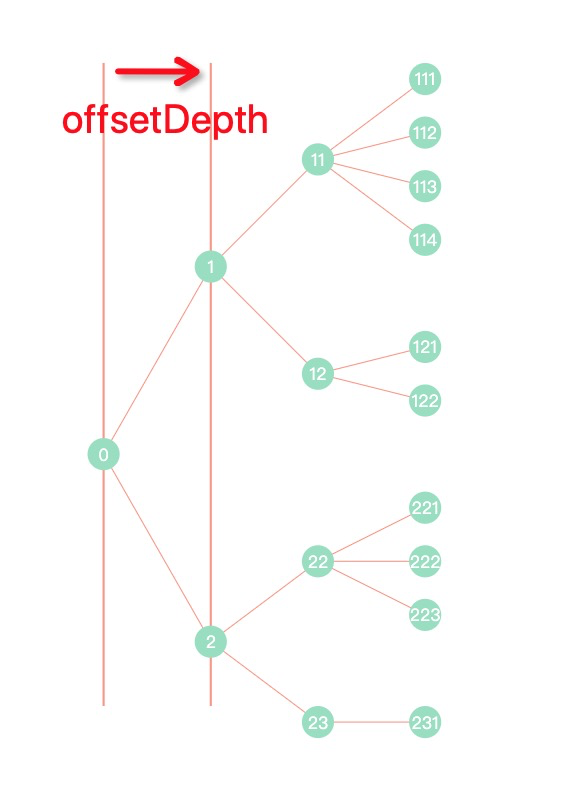
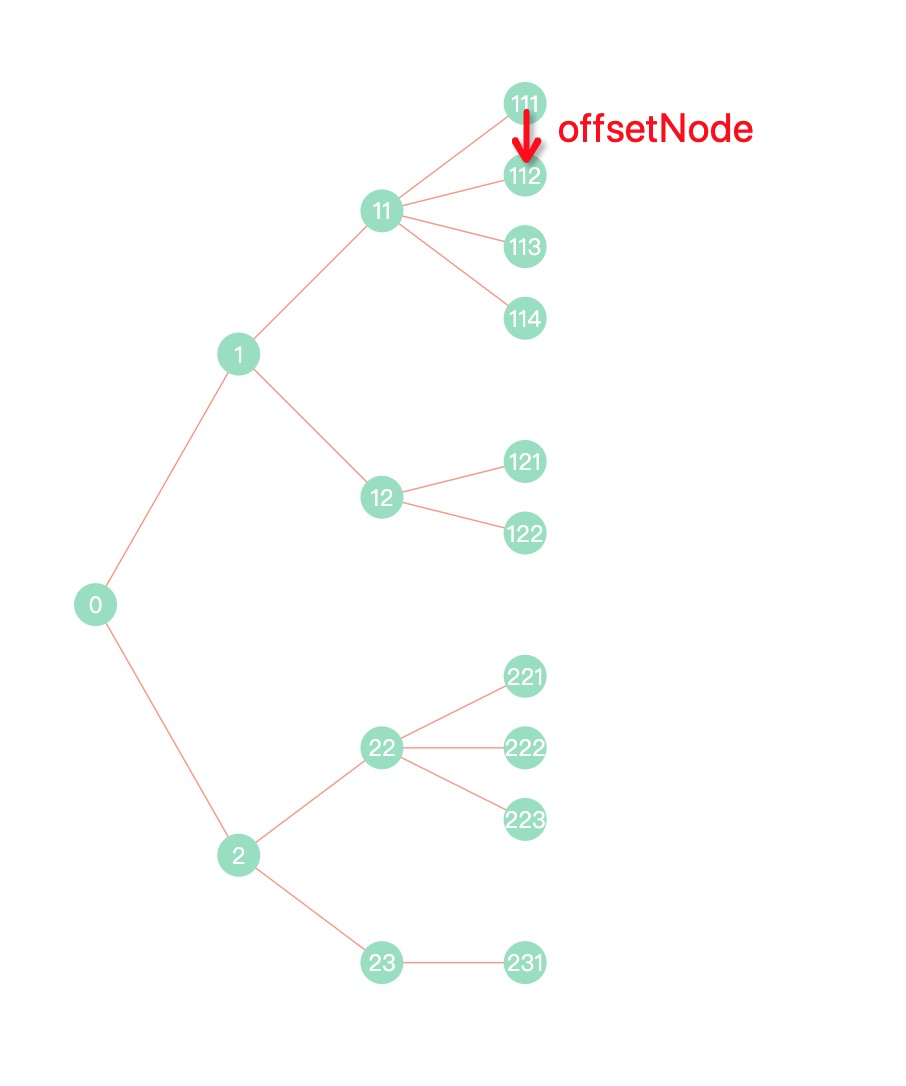
image.pngimage.png

  • direction: 树形排列方向，可选：’top’ | ‘right’ | ‘bottom’ | ‘left’，默认为 ‘right’ 向右排列
  1.     const { x, y } = origin;
  2.   const { offsetDepth, offsetNode } = offset;
  4.   const nodes: Array<INode> = [];
  5.   // 计算节点：从底层往上遍历
  6.   for (let i = matrix.length - 1; i > -1; i -= 1) {
  7.     let row = matrix[i];
  8.     let group = {};
  9.     let groupNodes: Array<INode> = [];
  11.     // 成组
  12.     row.forEach((item: INode) => {
  13.       if (item.parentId) {
  14.         group[item.parentId] = group[item.parentId] || [];
  15.         group[item.parentId].push(item);
  16.       }
  17.     });
  19.     Object.keys(group).forEach((item) => {
  20.       groupNodes = groupNodes.concat(group[item], [ ...new Array(1) ]) // 组与组之间填充空节点，用于分割
  21.     })
  23.     let positionNode = y; // 节点位置
  24.     let positionDepth = x; // 层级位置
  26.     let axisNode = 'y'; // 节点计算轴
  27.     let axisDepth = 'x'; // 层级计算轴
  29.     let positive = 1; // 排列顺序
  31.     if (direction === 'bottom' || direction === 'top') {
  32.       positionNode = x;
  33.       positionDepth = y;
  34.       axisNode = 'x';
  35.       axisDepth = 'y';
  36.     }
  38.     if (direction === 'left' || direction === 'top') positive = -1;
  40.     groupNodes.forEach((node: INode) => {
  41.       // 层级位置计算
  42.       if (node) {
  43.         node[axisDepth] = positionDepth + i * offsetDepth * positive;
  44.       }
  46.       // 节点位置计算
  47.       if (node && hash[node.id]) {
  48.         // 节点位置计算
  49.         if (typeof hash[node.id][axisNode] === 'undefined') {
  50.           node[axisNode] = positionNode; // 节点位置
  51.         }
  53.         // 节点位置修正
  54.         if (typeof hash[node.id][axisNode] !== 'undefined') {
  55.           node[axisNode] = hash[node.id][axisNode] / hash[node.id].children.length;
  56.         }
  58.         positionNode = node[axisNode] + offsetNode; // 增加间距
  60.         // 叠加子节点位置，存入父节点数据
  61.         if (node.parentId && hash[node.parentId]) {
  62.           if (typeof hash[node.parentId][axisNode] === 'undefined') {
  63.             hash[node.parentId][axisNode] = node[axisNode]
  64.           } else {
  65.             hash[node.parentId][axisNode] += node[axisNode]
  66.           }
  67.         }
  68.       }
  70.       // 空节点增加间距
  71.       if (!node) positionNode += offsetNode;
  73.       // 存入节点
  74.       if (node) nodes.push(node);
  75.     });
  76.   }

第四步：计算连接线

  1. interface ILink {
  2.   source: INode,
  3.   target: INode
  4. }
  1. // 计算连接线
  2. const links: Array<ILink> = [];
  3. const map = {};
  4. nodes.forEach(node => {
  5.   map[node.id] = node;
  6. })
  7. nodes.forEach(node => {
  8.   if (node.parentId && map[node.parentId]) {
  9.     links.push({ source: map[node.parentId], target: node});
  10.   }
  11. })
  12. // 返回图形数据
  13. return { links, nodes };

最终效果

这样就可以实现任意方向排列的树形图了

image.pngimage.png

image.pngimage.png