参考内容

[1] 📑 论文：https://epaperpress.com/sortsearch/download/skiplist.pdf
[2] 📙 漫画：https://www.jianshu.com/p/dc252b5efca6
[3] 🚀 博客：https://logi.im/algorithm/skiplist.html
[4] 💤 知乎：https://zhuanlan.zhihu.com/p/107835889

跳表概述

SkipList(跳跃表)来源于William Pugh于1990年发表的Skip Lists: A Probabilistic Alternative toBalanced Trees。

  • 跳跃表是由多层有序链表组合而成的，最底一层的链表保存了所有的数据，每向上的一层链表依次保存了下一层链表的部分数据。
  • 相邻的两层链表中元素相同的节点之间存在引用关系，一般是上层节点中存在一个指向下层节点的引用。
  • 跳跃表的目的在于提高了查询效率，同时也牺牲了一定的存储空间。

设计初衷：在某些场景下替代红黑树。

对比二叉查找树：维持结构平衡的成本比较低，完全依靠随机，并发性更强。而二叉查找树在多次插入删除后，需要rebalance来重新调整结构平衡。

算法简介

插入过程
方向：自底向上。
根据指定的随机Level向上层添加节点。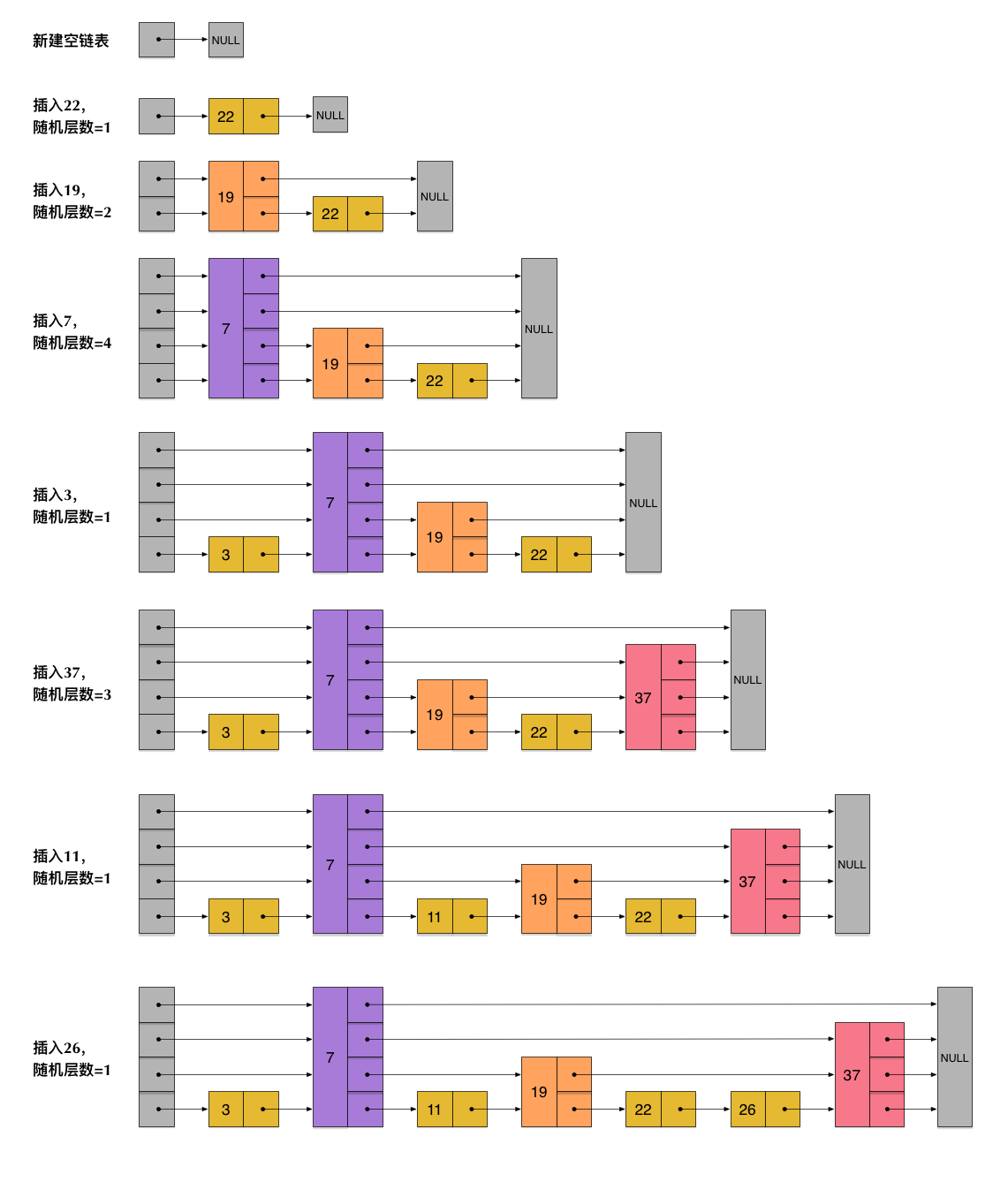
skiplist_insertions.png
每一个节点的层数（level）是随机出来的，而且新插入一个节点不会影响其他节点的层数。因此，插入操作只需要修改插入节点前后的指针，而不需要对很多节点都进行调整。

查找过程
方向：自顶向下，从左向右。
先在最上一层链表中从左向右查找，然后依次向下查找，直到最下一层的某个节点结束。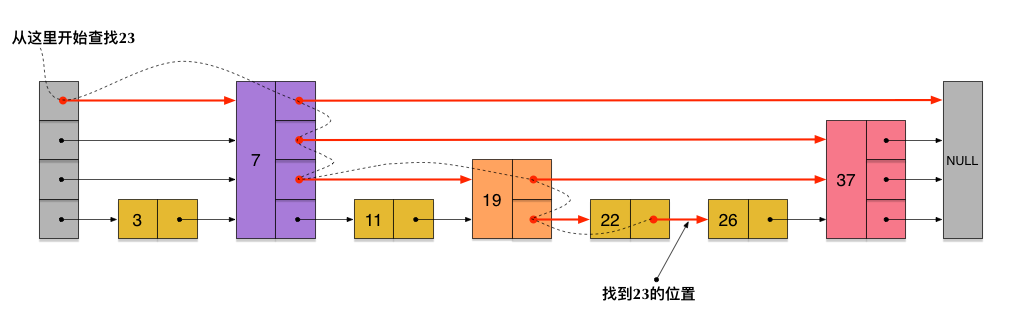
image.png

复杂度分析

假设总结点数为n，每2个节点间构建一个索引，少于2个节点的层无意义

层次 节点数
top 2
… …
k n / 2k
… …
2 n / 22
1 n / 2
0 n

SkipList - 图3
加上最后一层，则总层数为SkipList - 图4，1 ~ top层需要占用额外空间，节点数总和为
SkipList - 图5
所以跳表的空间复杂度为O(n)。

时间复杂度
插入和删除依赖查找，调整指针的时间复杂度为O(1)。
如果像上面那样建立最密索引，每层只需一次比较，因为层数为SkipList - 图6，所以最好时间复杂度为O(logn)。
不建立索引退化为链表，最差时间复杂度为O(n)。

Java实现

  1. /**
  2.  * @author KHighness
  3.  * @since 2021-07-22
  4.  * @apiNote 跳跃表
  5.  */
  6. public class SkipList<E extends Comparable<? super E>> {
  8.     private final static class Node<S> {
  9.         private final static class Level<T> {
  10.             /** 层后继 */
  11.             Node<T> backward;
  12.             /** 层跨度 */
  13.             int span;
  15.             public Level(Node<T> backward, int span) {
  16.                 this.backward = backward;
  17.                 this.span = span;
  18.             }
  19.         }
  21.         /** 数据 */
  22.         S item;
  23.         /** 前驱 */
  24.         Node<S> forward;
  25.         /** 层级数组 */
  26.         Level<S>[] levels;
  28.         public Node(S item, int level) {
  29.             this.item = item;
  30.             this.levels = new Level[level];
  31.         }
  32.     }
  34.     private static final int DEFAULT_LEVEL = 6;
  36.     /** 表头 */
  37.     private final Node<E> head;
  38.     /** 表尾 */
  39.     private Node<E> tail;
  40.     /** 最大层级 */
  41.     private final int maxLevel;
  42.     /** 总节点数 */
  43.     private long size;
  45.     public SkipList() {
  46.         this(DEFAULT_LEVEL);
  47.     }
  49.     public SkipList(int maxLevel) {
  50.         this.head = new Node<>(null, maxLevel);
  51.         this.tail = new Node<>(null, maxLevel);
  52.         this.maxLevel = maxLevel;
  53.         for (int i = 0; i < maxLevel; i++) {
  54.             head.levels[i] = new Node.Level<>(null, 0);
  55.         }
  56.     }
  58.     /**
  59.      * 查找并返回第level层小于elem的最后一个节点
  60.      * <p>同一level，从左向右
  61.      *
  62.      * @param start 起始搜寻点
  63.      * @param level 当前层级
  64.      * @param elem  比较数据
  65.      * @return 查找节点
  66.      */
  67.     private Node<E> getLevelPrev(Node<E> start, int level, E elem) {
  68.         while (start.levels[level].backward != null &&
  69.                 start.levels[level].backward.item.compareTo(elem) < 0) {
  70.             start = start.levels[level].backward;
  71.         }
  72.         return start;
  73.     }
  75.     /**
  76.      * 查找并返回包含指定数据的节点
  77.      * <p>自顶向下，从左向右
  78.      *
  79.      * @param elem 待查数据
  80.      * @return 找到则返回数据所在节点，未找到返回null
  81.      */
  82.     private Node<E> getNode(E elem) {
  83.         Node<E> prev = head;
  84.         for (int i = maxLevel - 1; i >= 0; i--) {
  85.             // 获取当前层级的前驱
  86.             prev = getLevelPrev(prev, i, elem);
  88.             // 确保存在后继
  89.             if (prev.levels[i] == null) continue;
  91.             Node<E> node = prev.levels[i].backward;
  92.             if (node != null && node.item.equals(elem)) {
  93.                 return node;
  94.             }
  95.         }
  96.         return null;
  97.     }
  99.     /**
  100.      * 生成并返回一个随机层级
  101.      *
  102.      * @return [1, maxLevel]之间的随机数
  103.      */
  104.     private int getRandomLevel() {
  105.         return (int) Math.ceil(Math.random() * (maxLevel - 1)) + 1;
  106.     }
  108.     /**
  109.      * 查找数据是否存在
  110.      *
  111.      * @param elem 待查数据
  112.      * @return true 代表存在，false 代表不存在
  113.      */
  114.     public boolean contains(E elem) {
  115.         return getNode(elem) != null;
  116.     }
  118.     /**
  119.      * 插入数据
  120.      * <ol>
  121.      * <li>根据新数据新建一个节点
  122.      * <li>生成节点的随机高度level
  123.      * <li>对于[1, level]每一层，设置层次数组中节点的后继和跨度
  124.      * <li>在最底层即第1层，插入节点，维护前驱和后继的关系
  125.      * </ol>
  126.      *
  127.      * @param elem 待插数据
  128.      * @return true 代表插入成功，false 代表数据已存在
  129.      */
  130.     public boolean insert(E elem) {
  131.         if (contains(elem)) return false;
  133.         int level = getRandomLevel();
  134.         Node<E> newNode = new Node<>(elem, level);
  136.         Node<E> prev = head;
  137.         for (int i = level - 1; i >= 0; i--) {
  138.             // 获得当前层级的前驱
  139.             prev = getLevelPrev(prev, i, elem);
  140.             Node.Level<E> prevLevel = prev.levels[i];
  141.             Node<E> next = prevLevel.backward;
  143.             // 第一层，将新节点插入到前驱和后继的中间，维护关系
  144.             if (i == 0) {
  145.                 if (next != null) {
  146.                     next.forward = newNode;
  147.                 } else {
  148.                     tail = newNode;
  149.                 }
  150.                 newNode.forward = prev;
  151.             }
  153.             // 增加后继的跨度
  154.             while (next != null) {
  155.                 next.levels[i].span++;
  156.                 next = next.levels[i].backward;
  157.             }
  159.             // 设置新节点的后继和跨度
  160.             newNode.levels[i] = new Node.Level<>(prevLevel.backward,
  161.                     prevLevel.span + 1);
  162.             // 更新前驱的后继
  163.             prevLevel.backward = newNode;
  164.         }
  166.         size++;
  167.         return true;
  168.     }
  170.     /**
  171.      * 删除数据
  172.      * <ol>
  173.      * <li>查找节点，获取到节点的层次数组的长度level
  174.      * <li>对于[1, level]每一层，更新层级数组中节点前驱的后继
  175.      * <li>在最底层即第1层，删除结点，维护前驱和后继的关系
  176.      * </ol>
  177.      *
  178.      * @param elem 待删数据
  179.      * @return true 代表删除成功，false 代表数据不存在
  180.      */
  181.     public boolean delete(E elem) {
  182.         Node<E> node = getNode(elem);
  183.         if (node == null) return false;
  185.         Node<E> prev = head;
  186.         int level = node.levels.length;
  187.         for (int i = level - 1; i >= 0; i--) {
  188.             // 获得当前层级的前驱
  189.             prev = getLevelPrev(prev, i, elem);
  191.             Node<E> next = node.levels[i].backward;
  193.             // 更新前驱的后继
  194.             prev.levels[i].backward = next;
  196.             // 更新后继的前驱或尾节点
  197.             if (i == 0) {
  198.                 if (next != null) {
  199.                     next.forward = prev;
  200.                 } else {
  201.                     tail = prev;
  202.                 }
  203.             }
  205.             // 减少后继的跨度
  206.             while (next != null) {
  207.                 next.levels[i].span--;
  208.                 next = next.levels[i].backward;
  209.             }
  210.         }
  212.         size--;
  213.         return true;
  214.     }
  216.     public void print() {
  217.         int maxItemLength = size == 0 ? 0 : tail.item.toString().length();
  218.         String format = "-> |%" + maxItemLength + "s| ";
  219.         StringBuilder gap = new StringBuilder("------");
  220.         for (int i = 0; i < maxItemLength; i++) gap.append('-');
  222.         System.out.printf("Size of list: %d\n", size);
  223.         for (int i = maxLevel - 1; i >= 0; i--) {
  224.             Node<E> node = head;
  226.             int nextSpan = 1;
  227.             if (node.levels[i].backward != null) {
  228.                 nextSpan = node.levels[i].backward.levels[i].span;
  229.             }
  231.             System.out.printf("|L%d| ", i);
  232.             while (node.levels[i].backward != null) {
  233.                 node = node.levels[i].backward;
  235.                 while (nextSpan++ < node.levels[0].span) {
  236.                     System.out.print(gap);
  237.                 }
  239.                 System.out.printf(format, node.item);
  240.             }
  242.             for (int j = nextSpan; j <= tail.levels[0].span; j++) {
  243.                 System.out.print(gap);
  244.             }
  245.             System.out.println("-> |NULL|");
  246.         }
  247.     }
  249. }

测试结果

测试代码：

  1. /**
  2.  * @author KHighness
  3.  * @since 2021-07-22
  4.  * @apiNote 跳跃表测试
  5.  */
  6. public class Main {
  8.     public static void main(String[] args) {
  9.         SkipList<Integer> list = new SkipList<>(7);
  11.         for (int i = 0; i < 10; i++) {
  12.             // [10, 100)
  13.             int item = (int) (Math.random() * 90) + 10;
  14.             list.insert(item);
  15.         }
  16.         list.print();
  18.         System.out.printf("\nInsertion of 88 succeeded? %s\n", list.insert(88));
  19.         System.out.printf("Insertion of 55 succeeded? %s\n", list.insert(55));
  20.         System.out.printf("Insertion of 11 succeeded? %s\n", list.insert(11));
  21.         System.out.printf("Insertion of 11 again succeeded? %s\n\n", list.insert(11));
  22.         list.print();
  24.         System.out.printf("\nDeletion of 88 succeeded? %s\n", list.delete(88));
  25.         System.out.printf("Deletion of 55 succeeded? %s\n", list.delete(55));
  26.         System.out.printf("Deletion of 11 succeeded? %s\n", list.delete(11));
  27.         System.out.printf("Deletion of 11 again succeeded? %s\n\n", list.delete(11));
  28.         list.print();
  29.     }
  30. }

运行结果：

  1. Size of list: 10
  2. |L6| ---------> |23| -------------------------> |58| ---------------------------------> |NULL|
  3. |L5| ---------> |23| -----------------> |46| -> |58| ---------------------------------> |NULL|
  4. |L4| ---------> |23| ---------> |43| -> |46| -> |58| ---------------------------------> |NULL|
  5. |L3| ---------> |23| -> |35| -> |43| -> |46| -> |58| -> |60| -------------------------> |NULL|
  6. |L2| -> |12| -> |23| -> |35| -> |43| -> |46| -> |58| -> |60| -> |61| -----------------> |NULL|
  7. |L1| -> |12| -> |23| -> |35| -> |43| -> |46| -> |58| -> |60| -> |61| -> |62| -> |65| -> |NULL|
  8. |L0| -> |12| -> |23| -> |35| -> |43| -> |46| -> |58| -> |60| -> |61| -> |62| -> |65| -> |NULL|
  10. Insertion of 88 succeeded? true
  11. Insertion of 55 succeeded? true
  12. Insertion of 11 succeeded? true
  13. Insertion of 11 again succeeded? false
  15. Size of list: 13
  16. |L6| -> |11| ---------> |23| -------------------------> |55| -> |58| -----------------------------------------> |NULL|
  17. |L5| -> |11| ---------> |23| -----------------> |46| -> |55| -> |58| -----------------------------------------> |NULL|
  18. |L4| -> |11| ---------> |23| ---------> |43| -> |46| -> |55| -> |58| -----------------------------------------> |NULL|
  19. |L3| -> |11| ---------> |23| -> |35| -> |43| -> |46| -> |55| -> |58| -> |60| ---------------------------------> |NULL|
  20. |L2| -> |11| -> |12| -> |23| -> |35| -> |43| -> |46| -> |55| -> |58| -> |60| -> |61| -------------------------> |NULL|
  21. |L1| -> |11| -> |12| -> |23| -> |35| -> |43| -> |46| -> |55| -> |58| -> |60| -> |61| -> |62| -> |65| -> |88| -> |NULL|
  22. |L0| -> |11| -> |12| -> |23| -> |35| -> |43| -> |46| -> |55| -> |58| -> |60| -> |61| -> |62| -> |65| -> |88| -> |NULL|
  24. Deletion of 88 succeeded? true
  25. Deletion of 55 succeeded? true
  26. Deletion of 11 succeeded? true
  27. Deletion of 11 again succeeded? false
  29. Size of list: 10
  30. |L6| ---------> |23| -------------------------> |58| ---------------------------------> |NULL|
  31. |L5| ---------> |23| -----------------> |46| -> |58| ---------------------------------> |NULL|
  32. |L4| ---------> |23| ---------> |43| -> |46| -> |58| ---------------------------------> |NULL|
  33. |L3| ---------> |23| -> |35| -> |43| -> |46| -> |58| -> |60| -------------------------> |NULL|
  34. |L2| -> |12| -> |23| -> |35| -> |43| -> |46| -> |58| -> |60| -> |61| -----------------> |NULL|
  35. |L1| -> |12| -> |23| -> |35| -> |43| -> |46| -> |58| -> |60| -> |61| -> |62| -> |65| -> |NULL|
  36. |L0| -> |12| -> |23| -> |35| -> |43| -> |46| -> |58| -> |60| -> |61| -> |62| -> |65| -> |NULL|
  38. Process finished with exit code 0