问题描述

谷歌的一道经典面试题 ——「双蛋问题」。

一个百层高大楼，从低层往下扔鸡蛋的时候，鸡蛋不会碎；从高层往下扔鸡蛋的时候，鸡蛋才会碎。
中间有一个临界楼层，在这个临界楼层以下的楼层扔，鸡蛋不会碎，超过这个楼层扔，鸡蛋会碎掉。

问题：如果拥有N个鸡蛋，最少要扔多少次，记为M，才能找出临界层？

思路解析

（1）N = 1
如果只有1个鸡蛋，那么只能从1层开始尝试，逐层尝试：

  1. 1、2、3、4、... 100

最坏的情况就是在第100层扔鸡蛋，鸡蛋才碎掉。
因此，N = 1的时候，M=100。

（2）N = +⚮
如果有无限个鸡蛋，这时候可以采用二分法进行尝试：
Two-Egg - 图1
因此，N=+⚮的时候，M= 7。

（3）N = 2
如果只有2个鸡蛋，让第一个鸡蛋A分别逐层尝试：

  1. 10、20、30、40、50、60、70、80、90、100

如果A在第「X」层没碎，但是在第「X+10」层碎了，那么让第二个鸡蛋B在区间(X, X+10)尝试：

  1. X+1、X+2、X+3、X+4、X+5、X+6、X+7、X+8、X+9

这个方法，最好情况下只需要扔10（A1+B9）次，最坏情况下需要扔19（A10+B9）次。
它不平均，原因是因为A它确定的间隔是等间隔的，B的尝试次数就是一样的，临界楼层越靠后，A的尝试次数就越多。

所以，我们需要思考，能不能让间隔变得不等，就是说，A每多扔一次，B的搜索区间就缩小一点，这样一来让A和B的总次数平均一点。
下面，调整A每次扔鸡蛋的间隔，第一次间隔为n，第二次间隔为n-1，第三次间隔为n-2，最后一次间隔为1层，尝试楼层如下：

  1. n、n+(n-1)、n+(n-1)+(n-2)、...、n(n+1)/2

从而，B的搜索区间长度就会呈现线性递减趋势：

  1. (n, n+(n-1))、(n+(n-1), n+(n-1)+(n-2))、...(n(n+1)/2-1, n(n+1)/2)

这样，A每多扔一次，B就少搜索一次，可以达到A和B的权衡。

Two-Egg - 图2
这种方法，可以让M稳定在14。

问题拓展

将问题拓展到更具有一般性的情况，可以参考「LeetCode 887. 鸡蛋掉落」。
简单描述：给定「n」层楼和「m」个鸡蛋，要求找到临界楼层「c」，最少需要尝试几次？

数学建模

求最值，不难想到经典DP（Dynamic Planning），打表格。
设尝试次数为「f」，F(i，j) 表示在「i」层楼和「j」个鸡蛋下找临界楼层的尝试次数。

只有1层楼或者只有1个鸡蛋的时候都只需要尝试1次，初始化表格如下：

i \ f \ j 1 2 3 4 5
1 1 1 1 1 1
2 1
3 1
4 1
5 1

无论如何，我们总要选择一层「k」，然后扔下去：

  • 如果碎了，那么「c」一定在「k」前面，同时鸡蛋数量减少一个，此时求解 f(k - 1，j - 1) ；
  • 如果不碎，那么「c」一定在「k」后面，但是鸡蛋数量没有变化，此时求解 f(n - k，j)。

在这两种情况下，我们需要取一个最大值，即：

Two-Egg - 图3

再加上这一次扔的次数，于是得到：

Two-Egg - 图4

这个「k」无法确定，于是我们通过枚举取值方案，取最小值：

Two-Egg - 图5

动态规划

根据上面的状态转移方程，可以写出动态规划对应的代码：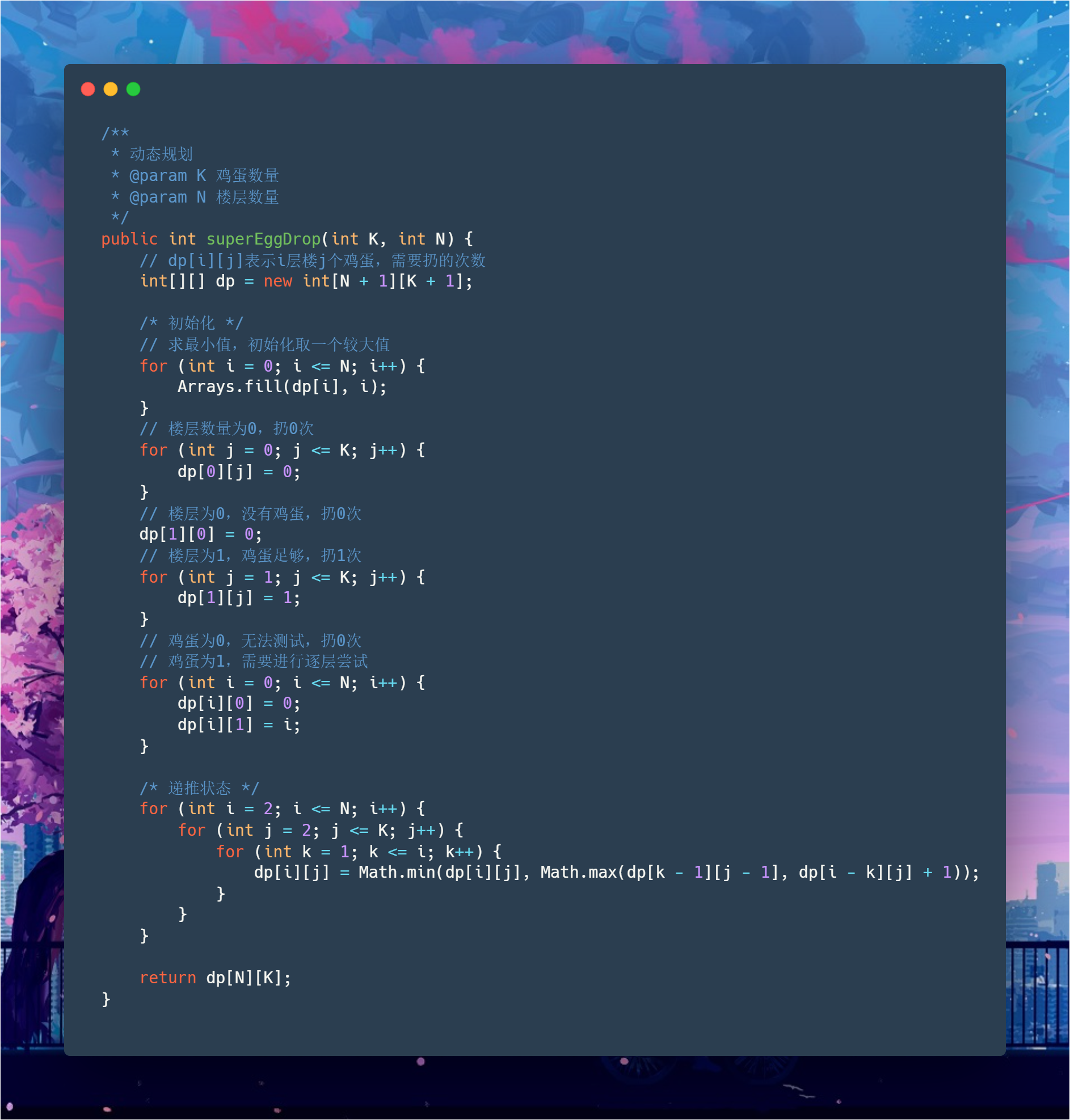
code1.png
这样写的话，时间复杂度达到Two-Egg - 图7，空间复杂度是Two-Egg - 图8。

二分优化

再看这个状态转移方程：

Two-Egg - 图9

设碎蛋函数f1 = f(k - 1, j - 1)，未碎函数f2 = f(i - k, j)，那么f=min(f1, f2)。
方程最外层的变量是「k」，它枚举了扔下鸡蛋的楼层的高度，这里它是函数的自变量，将「i」和「j」视为常数，那么：

  • 对于f1：k增大的时候，楼层大小越大，它的值就越大，所以碎蛋函数是个单调递增函数；
  • 对于f2：k增大的时候，楼层大小越小，它的值就越小，是个未碎函数是个单调递减函数。

TwoEgg.svg
这就类似于寻找数据峰值问题，可以参考「leetcode 162. 寻找峰值」。
code2.png
最终，代码便可以优化成如下：

  1.     /**
  2.      * @param K 鸡蛋数量
  3.      * @param N 楼层数量
  4.      */
  5.     public int superEggDrop(int K, int N) {
  6.         // dp[i][j]表示i层楼j个鸡蛋，需要扔的次数
  7.         int[][] dp = new int[N + 1][K + 1];
  9.         /* 初始化 */
  10.         // 求最小值，初始化取一个较大值
  11.         for (int i = 0; i <= N; i++) {
  12.             Arrays.fill(dp[i], i);
  13.         }
  14.         // 楼层数量为0，扔0次
  15.         for (int j = 0; j <= K; j++) {
  16.             dp[0][j] = 0;
  17.         }
  18.         // 楼层为0，没有鸡蛋，扔0次
  19.         dp[1][0] = 0;
  20.         // 楼层为1，鸡蛋足够，扔1次
  21.         for (int j = 1; j <= K; j++) {
  22.             dp[1][j] = 1;
  23.         }
  24.         // 鸡蛋为0，无法测试，扔0次
  25.         // 鸡蛋为1，需要进行逐层尝试
  26.         for (int i = 0; i <= N; i++) {
  27.             dp[i][0] = 0;
  28.             dp[i][1] = i;
  29.         }
  31.         /* 递推状态 */
  32.         for (int i = 2; i <= N; i++) {
  33.             for (int j = 2; j <= K; j++) {
  34.                 // 在区间[1, i]里确定一个最优值
  35.                 int l = 1, r = i;
  36.                 while (l < r) {
  37.                     int m = l + ((r - l + 1) >> 1);
  38.                     // 碎蛋函数，递增
  39.                     int f1 = dp[m - 1][j - 1];
  40.                     // 不碎函数，递减
  41.                     int f2 = dp[i - m][j];
  42.                     if (f1 > f2) {
  43.                         r = m - 1;
  44.                     } else {
  45.                         l = m;
  46.                     }
  47.                 }
  48.                 dp[i][j] = Math.max(dp[l - 1][j - 1], dp[i - l][j]) + 1;
  49.             }
  50.         }
  52.         return dp[N][K];
  53.     }

参考资料

[1] 📺 李永乐老师B站视频
[2] 📄 李维维哥哥力扣题解
[3] 💤 labuladong知乎专栏