数据结构

—栈—

概念

栈是一个线性结构，在计算机中是一个相当常见的数据结构。
栈的特点是只能在某一端添加或删除数据，遵循先进后出的原则

实现

每种数据结构都可以用很多种方式来实现，其实可以把栈看成是数组的一个子集，所以这里使用数组来实现

class Stack {
  constructor() {
    this.stack = []
  }
  push(item) {
    this.stack.push(item)
  }
  pop() {
    this.stack.pop()
  }
  peek() {
    return this.stack[this.getCount() - 1]
  }
  getCount() {
    return this.stack.length
  }
  isEmpty() {
    return this.getCount() === 0
  }
}

应用

选取了 LeetCode 上序号为 20 的题目
题意是匹配括号，可以通过栈的特性来完成这道题目

"([)]"
var isValid = function (s) {
  let map = {
    '(': -1,
    ')': 1,
    '[': -2,
    ']': 2,
    '{': -3,
    '}': 3
  }
  let stack = []
  for (let i = 0; i < s.length; i++) {
    if (map[s[i]] < 0) {
      stack.push(s[i])
    } else {
      let last = stack.pop()
      if (map[last] + map[s[i]] != 0) return false
    }
  }
  if (stack.length > 0) return false
  return true
};

—队列—

概念

队列是一个线性结构，特点是在某一端添加数据，在另一端删除数据，遵循先进先出的原则。

实现

这里会讲解两种实现队列的方式，分别是单链队列和循环队列。

单链队列

class Queue {
  constructor() {
    this.queue = []
  }
  enQueue(item) {
    this.queue.push(item)
  }
  deQueue() {
    return this.queue.shift()
  }
  getHeader() {
    return this.queue[0]
  }
  getLength() {
    return this.queue.length
  }
  isEmpty() {
    return this.getLength() === 0
  }
}

因为单链队列在出队操作的时候需要 O(n) 的时间复杂度，所以引入了循环队列。循环队列的出队操作平均是 O(1) 的时间复杂度。

优先队列

function PriorityQueue() {
    var items = [];
    function QueueElement(element, priority) { // {1}
        this.element = element;
        this.priority = priority;
    }
    this.enqueue = function (element, priority) {
        var queueElement = new QueueElement(element, priority);
        if (this.isEmpty()) {
            items.push(queueElement); // {2}
        } else {
            var added = false;
            for (var i = 0; i < items.length; i++) {
                if (queueElement.priority <
                    items[i].priority) {
                    items.splice(i, 0, queueElement); // {3}
                    added = true;
                    break; // {4}
                }
            }
            if (!added) { //{5}
                items.push(queueElement);
            }
        }
    };
    //其他方法和默认的Queue实现相同
}

默认的Queue类和PriorityQueue类实现上的区别是，要向PriorityQueue添加元素，需
要创建一个特殊的元素（行{1}）。这个元素包含了要添加到队列的元素（它可以是任意类型）
及其在队列中的优先级。
如果队列为空，可以直接将元素入列（行{2}）。否则，就需要比较该元素与其他元素的优
先级。当找到一个比要添加的元素的priority值更大（优先级更低）的项时，就把新元素插入
到它之前（根据这个逻辑，对于其他优先级相同，但是先添加到队列的元素，我们同样遵循先进
先出的原则）。要做到这一点，我们可以用第2章学习过的JavaScript的array类的splice方法。
一旦找到priority值更大的元素，就插入新元素（行{3}）并终止队列循环（行{4}）。这样，
队列也就根据优先级排序了。
如果要添加元素的priority值大于任何已有的元素，把它添加到队列的末尾就行了（行
{5}）：
var priorityQueue = new PriorityQueue();
priorityQueue.enqueue(“John”, 2);
priorityQueue.enqueue(“Jack”, 1);
priorityQueue.enqueue(“Camila”, 1);
priorityQueue.print();
以上代码是一个使用PriorityQueue类的示例。在下图中可以看到每条命令的结果（以上
代码的结果）：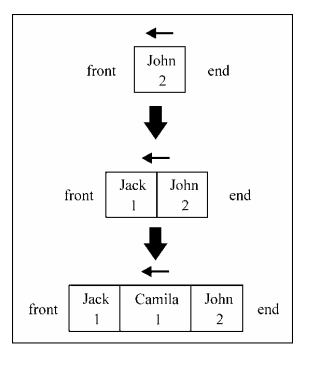

？循环队列(622. Design Circular Queue，自己题解中没有设置扩容)

class SqQueue { 
  constructor(length) {
    this.queue = new Array(length + 1)
    // 队头
    this.first = 0
    // 队尾
    this.last = 0
    // 当前队列大小
    this.size = 0
  }
  enQueue(item) {
    // 判断队尾 + 1 是否为队头
    // 如果是就代表需要扩容数组
    // % this.queue.length 是为了防止数组越界
    if (this.first === (this.last + 1) % this.queue.length) {
      this.resize(this.getLength() * 2 + 1)
    }
    this.queue[this.last] = item
    this.size++
    this.last = (this.last + 1) % this.queue.length
  }
  deQueue() {
    if (this.isEmpty()) {
      throw Error('Queue is empty')
    }
    let r = this.queue[this.first]
    this.queue[this.first] = null
    this.first = (this.first + 1) % this.queue.length
    this.size--
    // 判断当前队列大小是否过小
    // 为了保证不浪费空间，在队列空间等于总长度四分之一时
    // 且不为 2 时缩小总长度为当前的一半
    if (this.size === this.getLength() / 4 && this.getLength() / 2 !== 0) {
      this.resize(this.getLength() / 2)
    }
    return r
  }
  getHeader() {
    if (this.isEmpty()) {
      throw Error('Queue is empty')
    }
    return this.queue[this.first]
  }
  getLength() {
    return this.queue.length - 1
  }
  isEmpty() {
    return this.first === this.last
  }
  resize(length) {
    let q = new Array(length)
    for (let i = 0; i < length; i++) {
      q[i] = this.queue[(i + this.first) % this.queue.length]
    }
    this.queue = q
    this.first = 0
    this.last = this.size
  }
}

循环队列——击鼓传花

还有另一个修改版的队列实现，就是循环队列。循环队列的一个例子就是击鼓传花游戏（ Hot
Potato）。在这个游戏中，孩子们围成一个圆圈，把花尽快地传递给旁边的人。某一时刻传花停止，
这个时候花在谁手里，谁就退出圆圈结束游戏。重复这个过程，直到只剩一个孩子（胜者）。
在下面这个示例中，我们要实现一个模拟的击鼓传花游戏：

function hotPotato(nameList, num) {
    var queue = new Queue(); // {1}
    for (var i = 0; i < nameList.length; i++) {
        queue.enqueue(nameList[i]); // {2}
    }
    var eliminated = '';
    while (queue.size() > 1) {
        for (var i = 0; i < num; i++) {
            queue.enqueue(queue.dequeue()); // {3}
        }
        eliminated = queue.dequeue();// {4}
        console.log(eliminated + '在击鼓传花游戏中被淘汰。 ');
    }
    return queue.dequeue();// {5}
}
var names = ['John', 'Jack', 'Camila', 'Ingrid', 'Carl'];
var winner = hotPotato(names, 7);
console.log('胜利者： ' + winner);

—链表—

概念

链表是一个线性结构，同时也是一个天然的递归结构。链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。但是链表失去了数组随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大。

实现

单向链表

class ListNode {
  constructor(key) {
    this.next = null;
    this.key = key;
  }
}
class List {
  constructor() {
    this.head = null;
    this.length = 0;
  }
  static createNode(key) {
    return new ListNode(key);
  }
  // 往头部插入数据
  insert(node) {
    // 如果head后面有指向的节点
    if (this.head) {
      node.next = this.head;
    } else {
      node.next = null;
    }
    this.head = node;
    this.length++;
  }
  find(key) {
    let node = this.head;
    while (node !== null && node.key !== key) {
      node = node.next;
    }
    return node;
  }
  delete(node) {
    if (this.length === 0) {
      throw 'node is undefined';
    }
    if (node === this.head) {
      this.head = node.next;
      this.length--;
      return;
    }
    let prevNode = this.head;
    while (prevNode.next !== node) {
      prevNode = prevNode.next;
    }
    if (node.next === null) {
      prevNode.next = null;
    }
    if (node.next) {
      prevNode.next = node.next;
    }
    this.length--;
  }
}

双向链表

//封装双向链表
function DoublyLinkedList() {
  //内部类
  function Node(data) {
    this.data = data
    this.prev = null
    this.next = null
  }
  //属性
  this.head = null
  this.tail = null
  this.length = 0
  //1.append方法
  DoublyLinkedList.prototype.append = function (data) {
    //1.创建新的节点
    var newNode = new Node(data)
    //2.判断是否为第一个节点
    if (this.length == 0) {
      this.head = newNode
      this.tail = newNode
    } else {
      newNode.prev = this.tail
      this.tail.next = newNode
      this.tail = newNode
    }
    //3.length+1
    this.length += 1
  }
  //2.将链表转变为字符串形式
  //2.1 toString方法
  DoublyLinkedList.prototype.toString = function () {
    return this.backwardString()
  }
  //2.2 forwardString方法
  DoublyLinkedList.prototype.forwardString = function () {
    //1.定义变量
    var current = this.tail
    var resultString = ''
    //2.依次向后遍历,获取每一个节点
    while (current) {
      resultString += current.data + ''
      current = current.prev
    }
    return resultString
  }
  //2.3 backwardString方法
  DoublyLinkedList.prototype.backwardString = function () {
    //1.定义变量
    var current = this.head
    var resultString = ''
    //2.依次向后遍历,获取每一个节点
    while (current) {
      resultString += current.data + ' '
      current = current.next
    }
    return resultString
  }
  //3.insert方法
  DoublyLinkedList.prototype.insert = function (position, data) {
    //1.越界判断
    if (position < 0 || position > this.length) return false
    //2.创建新的节点
    var newNode = new Node(data)
    //3.判断原来列表是否为空
    if (this.length == 0) {
      this.head = newNode
      this.tail = newNode
    } else {
      if (position == 0) {//3.1 判断插入位置是否为0
        this.head.prev = newNode //原来的第一个节点.prev = newNode
        newNode.next = this.head// newNode.next= 原来的第一个节点
        this.head = newNode
      } else if (position == this.length) {//3.2判断插入位置是否为最后一位
        newNode.prev = this.tail
        this.tail.next = newNode
        this.tail = newNode
      } else {
        var current = this.head
        var index = 0
        while (index++ < position) {
          current = current.next//current为要插入点的后一个节点
        }
        newNode.next = current
        newNode.prev = current.prev
        current.prev.next = newNode
        current.prev = newNode
      }
    }
    //4.length+1
    this.length += 1
    console.log(this.length)
    return true
  }
  //4.get方法
  DoublyLinkedList.prototype.get = function (position) {
    //1.越界判断
    if (position < 0 || position >= this.length) return false
    //this.length/2 > position :从头向后遍历
    //this.length/2 < position :从后往前遍历 index-->position
    //2.获取元素
    var current = this.head
    var index = 0
    while (index++ < position) {
      current = current.next
    }
    console.log(current.data)
    return current.data
  }
  //5.indexOf方法
  DoublyLinkedList.prototype.indexOf = function (data) {
    //1.定义变量
    var current = this.head
    var index = 0
    //2.找到与data相同的节点
    while (current) {
      if (current.data == data) {
        return index
      }
      current = current.next
      index += 1
    }
    console.log(index)
    return -1
  }
  //6.update方法
  DoublyLinkedList.prototype.update = function (position, newData) {
    //1.越界判断
    if (position < 0 || position >= this.length) return false
    //2.查找节点
    var current = this.head
    var index = 0
    while (index++ < position) {
      current = current.next
    }
    current.data = newData
    return true
  }
  //7.removeAt方法
  DoublyLinkedList.prototype.removeAt = function (position) {
    //1.越界判断
    if (position < 0 || position >= this.length) return null
    //2.判断是否只有一个节点
    var current = this.head
    if (this.length == 1) {
      this.head = null
      this.tail = null
    } else {
      if (position == 0) {//判断是否是删除第一个节点
        this.head.next.prev = null
        this.head = this.head.next
      } else if (position == this.length - 1) {//是最后一个节点
        current = this.tail
        this.tail.prev.next = null
        this.tail = this.tail.prev
      } else {
        var index = 0
        while (index++ < position) {
          current = current.next
        }
        current.prev.next = current.next
        current.next.prev = current.prev
      }
    }
    //3.length-1
    this.length -= 1
    return current.data
  }
  //8.remove方法
  DoublyLinkedList.prototype.remove = function (data) {
    var index = this.indexOf(data)
    return this.removeAt(index)
  }
  DoublyLinkedList.prototype.isEmpty = function (data) {
    return this.length == 0
  }
  DoublyLinkedList.prototype.size = function (data) {
    return this.length
  }
  DoublyLinkedList.prototype.getHead = function (data) {
    return this.head.data
  }
  DoublyLinkedList.prototype.getTail = function (data) {
    return this.tail.data
  }
}
var doubly = new DoublyLinkedList()
doubly.append('abc')
doubly.append('def')
doubly.append('hjk')
console.log(doubly)
doubly.insert(0, '123')
doubly.insert(2, '456')
doubly.insert(5, '789')
console.log(doubly)
console.log(doubly.get(5))
console.log(doubly.indexOf('789'))
doubly.update(5, '012')
console.log(doubly)
console.log(doubly.removeAt(0))
console.log(doubly.removeAt(1))
console.log(doubly)
console.log(doubly.removeAt(3))
console.log(doubly)

集合

我们要实现的类就是以ECMAScript 6中Set类的实现为基础的

function Set() {
    var items = {};
    this.has = function (value) {
        return value in items;
    };
    this.add = function (value) {
        if (!this.has(value)) {
            items[value] = value; //{1}
            return true;
        }
        return false;
    };
    this.remove = function (value) {
        if (this.has(value)) {
            delete items[value]; //{2}
            return true;
        }
        return false;
    };
    this.clear = function () {
        items = {}; // {3}
    };
    this.size = function () {
        return Object.keys(items).length; //{4}
    };
    this.sizeLegacy = function () {
        var count = 0;
        for (var prop in items) { //{5}
            if (items.hasOwnProperty(prop)) //{6}
                ++count; //{7}
        }
        return count;
    };
    this.values = function () {
        return Object.keys(items);
    };
    //并集
    this.union = function (otherSet) {
        var unionSet = new Set(); //{1}
        var values = this.values(); //{2}
        for (var i = 0; i < values.length; i++) {
            unionSet.add(values[i]);
        }
        values = otherSet.values(); //{3}
        for (var i = 0; i < values.length; i++) {
            unionSet.add(values[i]);
        }
        return unionSet;
    };
    //交集
    this.intersection = function (otherSet) {
        var intersectionSet = new Set(); //{1}
        var values = this.values();
        for (var i = 0; i < values.length; i++) { //{2}
            if (otherSet.has(values[i])) { //{3}
                intersectionSet.add(values[i]); //{4}
            }
        }
        return intersectionSet;
    }
    //差集
    this.difference = function (otherSet) {
        var differenceSet = new Set(); //{1}
        var values = this.values();
        for (var i = 0; i < values.length; i++) { //{2}
            if (!otherSet.has(values[i])) { //{3}
                differenceSet.add(values[i]); //{4}
            }
        }
        return differenceSet;
    };
    //子集
    this.subset = function (otherSet) {
        if (this.size() > otherSet.size()) { //{1}
            return false;
        } else {
            var values = this.values();
            for (var i = 0; i < values.length; i++) { //{2}
                if (!otherSet.has(values[i])) { //{3}
                    return false; //{4}
                }
            }
            return true; //{5}
        }
    };
}

字典

集合以[值，值]的形式存储元素，字 典则是以[键，值]的形式来存储元素。字典也称作映射。

//字典数据结构
    function Dictionary(){
        this.items = {};
        //检查是否有某一个键
        this.has = function(key){
            return this.items.hasOwnProperty(key);
        }
        //为字典添加某一个值
        this.set = function(key,val){
            this.items[key] = val;
        }
        //删除某一个键
        this.delete = function(key){
            if(this.has(key)){
                delete this.items[key];
                return true;
            }
            return false;
        }
        //查找某一特定项
        this.get = function(key){
            return this.has(key) ? this.items[key] : undefined; 
        }
        //返回字典中的所有值
        this.values = function(){
            var res = [];
            for(var prop in this.items){
                if(this.has(prop)){
                    res.push(this.items[prop]);
                }
            }
            return res;
        }
        //清空字典
        this.clear = function(){
            this.items = {};
        }
        //获取字典的长度
        this.size = function(){
            return Object.keys(this.items).length;
        }
        //获取字典所有的键
        this.keys = function(){
            return Object.keys(this.items);
        }
        //返回字典本身
        this.getItems = function(){
            return this.items;
        }
    }

ES6中的Set和Map

Set

上面代码通过add()方法向 Set 结构加入成员，结果表明 Set 结构不会添加重复的值。
Set函数可以接受一个数组（或者具有 iterable 接口的其他数据结构）作为参数，用来初始化。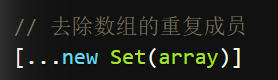

向 Set 加入值的时候，不会发生类型转换，所以5和"5"是两个不同的值。

WeakSet

WeakSet 结构与 Set 类似，也是不重复的值的集合。但是，它与 Set 有两个区别。
首先，WeakSet 的成员只能是对象，而不能是其他类型的值。
其次，WeakSet 中的对象都是弱引用，即垃圾回收机制不考虑 WeakSet 对该对象的引用，也就是说，如果其他对象都不再引用该对象，那么垃圾回收机制会自动回收该对象所占用的内存，不考虑该对象还存在于 WeakSet 之中。

Map

它类似于对象，也是键值对的集合，但是“键”的范围不限于字符串，各种类型的值（包括对象）都可以当作键。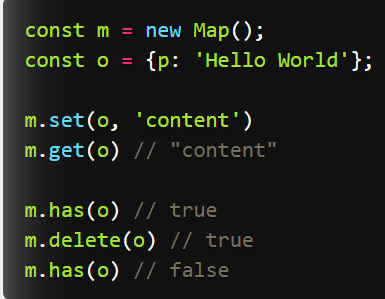

—两种添加元素的方式
事实上，不仅仅是数组，任何具有 Iterator 接口、且每个成员都是一个双元素的数组的数据结构（详见《Iterator》一章）都可以当作Map构造函数的参数。这就是说，Set和Map都可以用来生成新的 Map。

只有对同一个对象的引用，Map 结构才将其视为同一个键。这一点要非常小心。

const map = new Map();
map.set(['a'], 555);
map.get(['a']) // undefined

如果 Map 的键是一个简单类型的值（数字、字符串、布尔值），则只要两个值严格相等(===)，Map 将其视为一个键，比如0和-0就是一个键，布尔值true和字符串true则是两个不同的键。另外，undefined和null也是两个不同的键。虽然NaN不严格相等于自身，但 Map 将其视为同一个键。

WeakMap

WeakMap与Map的区别有两点。
首先，WeakMap只接受对象作为键名（null除外），不接受其他类型的值作为键名。

其次，WeakMap的键名所指向的对象，不计入垃圾回收机制。WeakMap 弱引用的只是键名，而不是键值。键值依然是正常引用。

const e1 = document.getElementById('foo');
const e2 = document.getElementById('bar');
const arr = [
  [e1, 'foo 元素'],
  [e2, 'bar 元素'],
];

上面代码中，e1和e2是两个对象，我们通过arr数组对这两个对象添加一些文字说明。这就形成了arr对e1和e2的引用。
一旦不再需要这两个对象，我们就必须手动删除这个引用，否则垃圾回收机制就不会释放e1和e2占用的内存。

// 不需要 e1 和 e2 的时候
// 必须手动删除引用
arr [0] = null;
arr [1] = null;

上面这样的写法显然很不方便。一旦忘了写，就会造成内存泄露。
WeakMap 就是为了解决这个问题而诞生的，它的键名所引用的对象都是弱引用，即垃圾回收机制不将该引用考虑在内。因此，只要所引用的对象的其他引用都被清除，垃圾回收机制就会释放该对象所占用的内存。也就是说，一旦不再需要，WeakMap 里面的键名对象和所对应的键值对会自动消失，不用手动删除引用。

散列表HashTable

给定一个key参数，我们就能根据组成key的每个字符的ASCII码值的和得到一个数字。所以， 首先需要一个变量来存储这个总和（行{1}）。然后，遍历key（行{2}）并将从ASCII表中查到 的每个字符对应的ASCII值加到hash变量中（可以使用JavaScript的String类中的charCodeAt 方法——行{3}）。后，返回hash值。为了得到比较小的数值，我们会使用hash值和一个任意 数做除法的余数（mod）。

function HashTable() {     
  var table = []; 
}
var loseloseHashCode = function (key) {     var hash = 0;                          //{1}     for (var i = 0; i < key.length; i++) { //{2}         hash += key.charCodeAt(i);         //{3}     }     return hash % 37; //{4} };

Jonathan、Jamie和Sue有相同的散列值，也就是5。由于Sue是后一个被添加的，Sue 将是在HashTable实例中占据位置5的元素。首先，Jonathan会占据这个位置，然后Jamie会覆 盖它，然后Sue会再次覆盖。这对于其他发生冲突的元素来说也是一样的。
使用一个数据结构来保存数据的目的显然不是去丢失这些数据，而是通过某种方法将它们全部保存起来。因此，当这种情况发生的时候就要去解决它。处理冲突有几种方法：分离链接、线 性探查和双散列法。在本书中，我们会介绍前两种方法

分离链接

为了实现一个使用了分离链接的HashTable实例，我们需要一个新的辅助类来表示将要加入 LinkedList实例的元素。我们管它叫ValuePair类（在HashTable类内部定义）：
var ValuePair = function(key, value){ this.key = key; this.value = value;

this.toString = function() { return ‘[‘ + this.key + ‘ - ‘ + this.value + ‘]’; } };
这个类只会将key和value存储在一个Object实例中。我们也重写了toString方法，以便 之后在浏览器控制台中输出结果。
图
(1) put方法
我们来实现第一个方法，put方法，代码如下：
this.put = function(key, value){ var position = loseloseHashCode(key);

if (table[position] == undefined) { //{1} table[position] = new LinkedList(); } table[position].append(new ValuePair(key, value)); //{2} }; 在这个方法中，将验证要加入新元素的位置是否已经被占据（行{1}）。如果这个位置是第 一次被加入元素，我们会在这个位置上初始化一个LinkedList类的实例（你已经在第5章中学 习过）。然后，使用第5章中实现的append方法向LinkedList实例中添加一个ValuePair实例 （键和值）（行{2}）。
(2) get方法
然后，我们实现用来获取特定值的get方法：
this.get = function(key) { var position = loseloseHashCode(key);

if (table[position] !== undefined){ //{3}

//遍历链表来寻找键/值 var current = table[position].getHead(); //{4}

while(current.next){ //{5} if (current.element.key === key){ //{6} return current.element.value; //{7} } current = current.next; //{8} }

//检查元素在链表第一个或最后一个节点的情况 if (current.element.key === key){ //{9} return current.element.value; } } return undefined; //{10} }; 我们要做的第一个验证，是确定在特定的位置上是否有元素存在（行{3}）。如果没有，则 返回一个undefined表示在HashTable实例中没有找到这个值（行{10}）。如果在这个位置上有 值存在，我们知道这是一个LinkedList实例。现在要做的是遍历这个链表来寻找我们需要的元 素。在遍历之前先要获取链表表头的引用（行{4}），然后就可以从链表的头部遍历到尾部（行 {5}，current.next将会是null）

(3) remove方法
使用分离链接法从HashTable实例中移除一个元素和之前在本章实现的remove方法有一些 不同。现在使用的是链表，我们需要从链表中移除一个元素。来看看remove方法的实现：
this.remove = function(key){ var position = loseloseHashCode(key);

if (table[position] !== undefined){

var current = table[position].getHead(); while(current.next){ if (current.element.key === key){ //{11} table[position].remove(current.element); //{12} if (table[position].isEmpty()){ //{13} table[position] = undefined; //{14} } return true; //{15} } current = current.next; }

// 检查是否为第一个或最后一个元素 if (current.element.key === key){ //{16} table[position].remove(current.element); if (table[position].isEmpty()){ table[position] = undefined; } return true; } }

return false; //{17} }; 在remove方法中，我们使用和get方法一样的步骤找到要找的元素。遍历LinkedList实例 时，如果链表中的current元素就是要找的元素（行{11}），使用remove方法将其从链表中移 除。然后进行一步额外的验证：如果链表为空了（行{13}——链表中不再有任何元素了），就将 散列表这个位置的值设为undefined（行{14}），

线性探查

另一种解决冲突的方法是线性探查。当想向表中某个位置加入一个新元素的时候，如果索引 为index的位置已经被占据了，就尝试index+1的位置。如果index+1的位置也被占据了，就尝试 index+2的位置，以此类推。
(1) put方法
让我们继续实现需要重写的三个方法。第一个是put方法：
this.put = function(key, value){ var position = loseloseHashCode(key); // {1}

if (table[position] == undefined) { // {2} table[position] = new ValuePair(key, value); // {3} } else { var index = ++position; // {4} while (table[index] != undefined){ // {5} index++; // {6} } table[index] = new ValuePair(key, value); // {7} } };
和之前一样，先获得由散列函数生成的位置（行{1}），然后验证这个位置是否有元素存在 （如果这个位置被占据了，将会通过行{2}的验证）。如果没有元素存在，就在这个位置加入新元 素（行{3}——一个ValuePair的实例）。

如果这个位置已经被占据了，需要找到下一个没有被占据的位置（position的值是 undefined），因此我们声明一个index变量并赋值为position+1（行{4}——在变量名前使用 自增运算符++会先递增变量值然后再将其赋值给index）。然后验证这个位置是否被占据（行 {5}），如果被占据了，继续将index递增（行{6}），直到找到一个没有被占据的位置。然后要 做的，就是将值分配到这个位置（行{7}）。
(2) get方法 现在插入了所有的元素，让我们实现get方法来获取它们的值吧：
this.get = function(key) { var position = loseloseHashCode(key);

if (table[position] !== undefined){ //{8} if (table[position].key === key) { //{9} return table[position].value; //{10} } else { var index = ++position; while (table[index] === undefined || table[index].key !== key){ //{11} index++; } if (table[index].key === key) { //{12} return table[index].value; //{13} } } } return undefined; //{14} }; 要获得一个键对应的值，先要确定这个键存在（行{8}）。如果这个键不存在，说明要查找 的值不在散列表中，因此可以返回undefined（行{14}）。如果这个键存在，需要检查我们要找 的值是否就是这个位置上的值（行{9}）。如果是，就返回这个值（行{10}）。
如果不是，就在散列表中的下一个位置继续查找，直到找到一个键值与我们要找的键值相同 的元素（行{11}）。然后，验证一下当前项就是我们要找的项（行{12}——只是为了确认一下） 并且将它的值返回（行{13}）。
我们无法确定要找的元素实际上在哪个位置，这就是使用ValuePair来表示HashTable元 素的原因。 (3) remove方法
remove方法和get方法基本相同，不同之处在于行{10}和{13}，它们将会由下面的代码代替：

table[index] = undefined; 要移除一个元素，只需要给其赋值为undefined，来表示这个位置不再被占据并且可以在必 要时接受一个新元素。

—树—

二叉树

树拥有很多种结构，二叉树是树中最常用的结构，同时也是一个天然的递归结构。
二叉树拥有一个根节点，每个节点至多拥有两个子节点，分别为：左节点和右节点。树的最底部节点称之为叶节点，当一颗树的叶数量数量为满时，该树可以称之为满二叉树。

二分搜索树(BST)

二分搜索树也是二叉树，拥有二叉树的特性。但是区别在于二分搜索树每个节点的值都比他的左子树的值大，比右子树的值小。
这种存储方式很适合于数据搜索。如下图所示，当需要查找 6 的时候，因为需要查找的值比根节点的值大，所以只需要在根节点的右子树上寻找，大大提高了搜索效率。

实现

class Node {
  constructor(value) {
    this.value = value
    this.left = null
    this.right = null
  }
}
class BST {
  constructor() {
    this.root = null
    this.size = 0
  }
  getSize() {
    return this.size
  }
  isEmpty() {
    return this.size === 0
  }
  addNode(v) {
    this.root = this._addChild(this.root, v)
  }
  // 添加节点时，需要比较添加的节点值和当前
  // 节点值的大小
  _addChild(node, v) {
    if (!node) {
      this.size++
      return new Node(v)
    }
    if (node.value > v) {
      node.left = this._addChild(node.left, v)
    } else if (node.value < v) {
      node.right = this._addChild(node.right, v)
    }
    return node
  }
}

以上是最基本的二分搜索树实现。

树的遍历

对于树的遍历来说，有三种遍历方法，分别是先序遍历、中序遍历、后序遍历。三种遍历的区别在于何时访问节点。在遍历树的过程中，每个节点都会遍历三次，分别是遍历到自己，遍历左子树和遍历右子树。如果需要实现先序遍历，那么只需要第一次遍历到节点时进行操作即可。

// 先序遍历可用于打印树的结构
// 先序遍历先访问根节点，然后访问左节点，最后访问右节点。
preTraversal() {
  this._pre(this.root)
}
_pre(node) {
  if (node) {
    console.log(node.value)
    this._pre(node.left)
    this._pre(node.right)
  }
}
// 中序遍历可用于排序
// 对于 BST 来说，中序遍历可以实现一次遍历就
// 得到有序的值
// 中序遍历表示先访问左节点，然后访问根节点，最后访问右节点。
midTraversal() {
  this._mid(this.root)
}
_mid(node) {
  if (node) {
    this._mid(node.left)
    console.log(node.value)
    this._mid(node.right)
  }
}
// 后序遍历可用于先操作子节点
// 再操作父节点的场景
// 后序遍历表示先访问左节点，然后访问右节点，最后访问根节点。
backTraversal() {
  this._back(this.root)
}
_back(node) {
  if (node) {
    this._back(node.left)
    this._back(node.right)
    console.log(node.value)
  }
}

以上的这几种遍历都可以称之为深度遍历，对应的还有种遍历叫做广度遍历，也就是一层层地遍历树。

对于广度遍历来说，我们需要利用之前讲过的队列结构来完成。

breadthTraversal() {
  if (!this.root) return null
  let q = new Queue()
  // 将根节点入队
  q.enQueue(this.root)
  // 循环判断队列是否为空，为空
  // 代表树遍历完毕
  while (!q.isEmpty()) {
    // 将队首出队，判断是否有左右子树
    // 有的话，就先左后右入队
    let n = q.deQueue()
    console.log(n.value)
    if (n.left) q.enQueue(n.left)
    if (n.right) q.enQueue(n.right)
  }
}

接下来先介绍如何在树中寻找最小值或最大数。因为二分搜索树的特性，所以最小值一定在根节点的最左边，最大值相反

getMin() {
  return this._getMin(this.root).value
}
_getMin(node) {
  if (!node.left) return node
  return this._getMin(node.left)
}
getMax() {
  return this._getMax(this.root).value
}
_getMax(node) {
  if (!node.right) return node
  return this._getMin(node.right)
}

向上取整和向下取整
**排名
**删除节点

—AVL 树—

概念

二分搜索树实际在业务中是受到限制的，因为并不是严格的 O(logN)，在极端情况下会退化成链表，比如加入一组升序的数字就会造成这种情况。
AVL 树改进了二分搜索树，在 AVL 树中任意节点的左右子树的高度差都不大于 1，这样保证了时间复杂度是严格的 O(logN)。基于此，对 AVL 树增加或删除节点时可能需要旋转树来达到高度的平衡。

实现

因为 AVL 树是改进了二分搜索树，所以部分代码是于二分搜索树重复的，对于重复内容不作再次解析。
对于 AVL 树来说，添加节点会有四种情况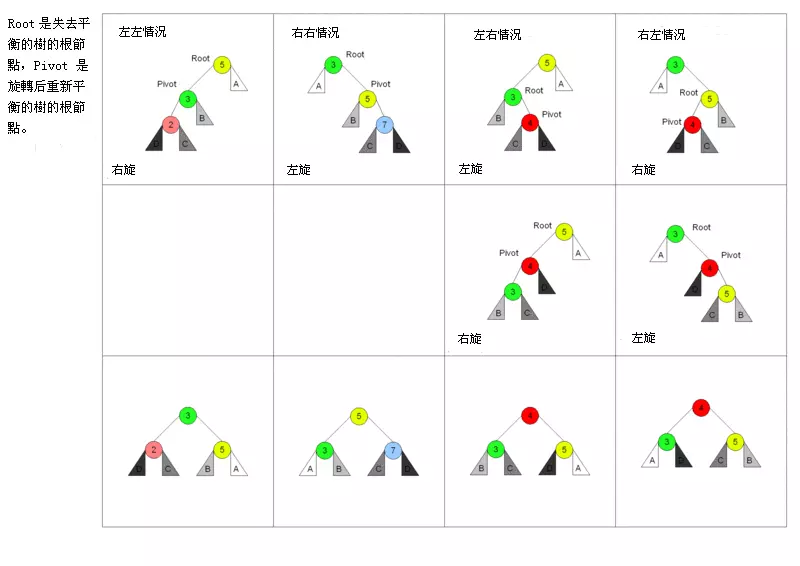

对于左左情况来说，新增加的节点位于节点 2 的左侧，这时树已经不平衡，需要旋转。因为搜索树的特性，节点比左节点大，比右节点小，所以旋转以后也要实现这个特性。
旋转之前：new < 2 < C < 3 < B < 5 < A，右旋之后节点 3 为根节点，这时候需要将节点 3 的右节点加到节点 5 的左边，最后还需要更新节点的高度。
对于右右情况来说，相反于左左情况，所以不再赘述。
对于左右情况来说，新增加的节点位于节点 4 的右侧。对于这种情况，需要通过两次旋转来达到目的。
首先对节点的左节点左旋，这时树满足左左的情况，再对节点进行一次右旋就可以达到目的。

class Node {
  constructor(value) {
    this.value = value
    this.left = null
    this.right = null
    this.height = 1
  }
}
class AVL {
  constructor() {
    this.root = null
  }
  addNode(v) {
    this.root = this._addChild(this.root, v)
  }
  _addChild(node, v) {
    if (!node) {
      return new Node(v)
    }
    if (node.value > v) {
      node.left = this._addChild(node.left, v)
    } else if (node.value < v) {
      node.right = this._addChild(node.right, v)
    } else {
      node.value = v
    }
    node.height =
      1 + Math.max(this._getHeight(node.left), this._getHeight(node.right))
    let factor = this._getBalanceFactor(node)
    // 当需要右旋时，根节点的左树一定比右树高度高
    if (factor > 1 && this._getBalanceFactor(node.left) >= 0) {
      return this._rightRotate(node)
    }
    // 当需要左旋时，根节点的左树一定比右树高度矮
    if (factor < -1 && this._getBalanceFactor(node.right) <= 0) {
      return this._leftRotate(node)
    }
    // 左右情况
    // 节点的左树比右树高，且节点的左树的右树比节点的左树的左树高
    if (factor > 1 && this._getBalanceFactor(node.left) < 0) {
      node.left = this._leftRotate(node.left)
      return this._rightRotate(node)
    }
    // 右左情况
    // 节点的左树比右树矮，且节点的右树的右树比节点的右树的左树矮
    if (factor < -1 && this._getBalanceFactor(node.right) > 0) {
      node.right = this._rightRotate(node.right)
      return this._leftRotate(node)
    }
    return node
  }
  _getHeight(node) {
    if (!node) return 0
    return node.height
  }
  _getBalanceFactor(node) {
    return this._getHeight(node.left) - this._getHeight(node.right)
  }
  // 节点右旋
  //           5                    2
  //         /   \                /   \
  //        2     6   ==>       1      5
  //       /  \               /       /  \
  //      1    3             new     3    6
  //     /
  //    new
  _rightRotate(node) {
    // 旋转后新根节点
    let newRoot = node.left
    // 需要移动的节点
    let moveNode = newRoot.right
    // 节点 2 的右节点改为节点 5
    newRoot.right = node
    // 节点 5 左节点改为节点 3
    node.left = moveNode
    // 更新树的高度
    node.height =
      1 + Math.max(this._getHeight(node.left), this._getHeight(node.right))
    newRoot.height =
      1 +
      Math.max(this._getHeight(newRoot.left), this._getHeight(newRoot.right))
    return newRoot
  }
  // 节点左旋
  //           4                    6
  //         /   \                /   \
  //        2     6   ==>       4      7
  //             /  \         /   \      \
  //            5     7      2     5      new
  //                   \
  //                    new
  _leftRotate(node) {
    // 旋转后新根节点
    let newRoot = node.right
    // 需要移动的节点
    let moveNode = newRoot.left
    // 节点 6 的左节点改为节点 4
    newRoot.left = node
    // 节点 4 右节点改为节点 5
    node.right = moveNode
    // 更新树的高度
    node.height =
      1 + Math.max(this._getHeight(node.left), this._getHeight(node.right))
    newRoot.height =
      1 +
      Math.max(this._getHeight(newRoot.left), this._getHeight(newRoot.right))
    return newRoot
  }
}

—Trie—

概念

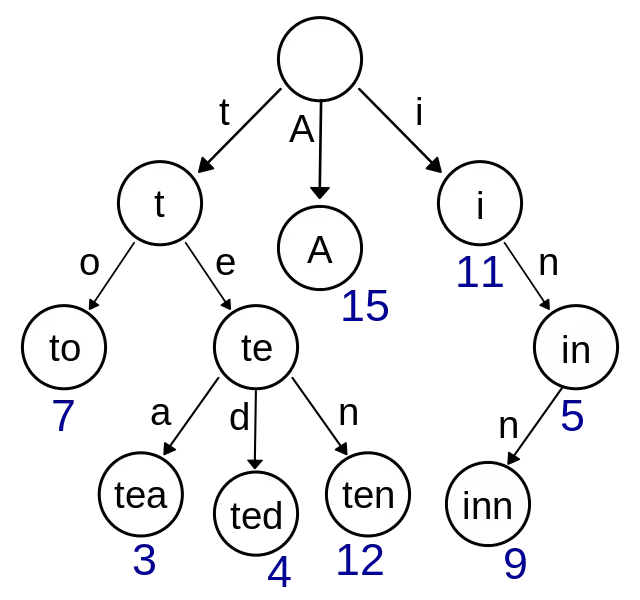
在计算机科学，trie，又称前缀树或字典树，是一种有序树，用于保存关联数组，其中的键通常是字符串。
简单点来说，这个结构的作用大多是为了方便搜索字符串，该树有以下几个特点

• 根节点代表空字符串，每个节点都有 N（假如搜索英文字符，就有 26 条） 条链接，每条链接代表一个字符
• 节点不存储字符，只有路径才存储，这点和其他的树结构不同
• 从根节点开始到任意一个节点，将沿途经过的字符连接起来就是该节点对应的字符串

、

实现

总得来说 Trie 的实现相比别的树结构来说简单的很多，实现就以搜索英文字符为例。

class TrieNode {
  constructor() {
    // 代表每个字符经过节点的次数
    this.path = 0
    // 代表到该节点的字符串有几个
    this.end = 0
    // 链接
    this.next = new Array(26).fill(null)
  }
}
class Trie {
  constructor() {
    // 根节点，代表空字符
    this.root = new TrieNode()
  }
  // 插入字符串
  insert(str) {
    if (!str) return
    let node = this.root
    for (let i = 0; i < str.length; i++) {
      // 获得字符先对应的索引
      let index = str[i].charCodeAt() - 'a'.charCodeAt()
      // 如果索引对应没有值，就创建
      if (!node.next[index]) {
        node.next[index] = new TrieNode()
      }
      node.path += 1
      node = node.next[index]
    }
    node.end += 1
  }
  // 搜索字符串出现的次数
  search(str) {
    if (!str) return
    let node = this.root
    for (let i = 0; i < str.length; i++) {
      let index = str[i].charCodeAt() - 'a'.charCodeAt()
      // 如果索引对应没有值，代表没有需要搜素的字符串
      if (!node.next[index]) {
        return 0
      }
      node = node.next[index]
    }
    return node.end
  }
  // 删除字符串
  delete(str) {
    if (!this.search(str)) return
    let node = this.root
    for (let i = 0; i < str.length; i++) {
      let index = str[i].charCodeAt() - 'a'.charCodeAt()
      // 如果索引对应的节点的 Path 为 0，代表经过该节点的字符串
      // 已经一个，直接删除即可
      if (--node.next[index].path == 0) {
        node.next[index] = null
        return
      }
      node = node.next[index]
    }
    node.end -= 1
  }
}

—并查集—

概念

并查集是一种特殊的树结构，用于处理一些不交集的合并及查询问题。该结构中每个节点都有一个父节点，如果只有当前一个节点，那么该节点的父节点指向自己。
这个结构中有两个重要的操作，分别是：

• Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
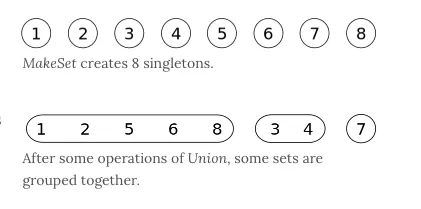
• Union：将两个子集合并成同一个集合。

实现

class DisjointSet {
  // 初始化样本
  constructor(count) {
    // 初始化时，每个节点的父节点都是自己
    this.parent = new Array(count)
    // 用于记录树的深度，优化搜索复杂度
    this.rank = new Array(count)
    for (let i = 0; i < count; i++) {
      this.parent[i] = i
      this.rank[i] = 1
    }
  }
  find(p) {
    // 寻找当前节点的父节点是否为自己，不是的话表示还没找到
    // 开始进行路径压缩优化
    // 假设当前节点父节点为 A
    // 将当前节点挂载到 A 节点的父节点上，达到压缩深度的目的
    while (p != this.parent[p]) {
      this.parent[p] = this.parent[this.parent[p]]
      p = this.parent[p]
    }
    return p
  }
  isConnected(p, q) {
    return this.find(p) === this.find(q)
  }
  // 合并
  union(p, q) {
    // 找到两个数字的父节点
    let i = this.find(p)
    let j = this.find(q)
    if (i === j) return
    // 判断两棵树的深度，深度小的加到深度大的树下面
    // 如果两棵树深度相等，那就无所谓怎么加
    if (this.rank[i] < this.rank[j]) {
      this.parent[i] = j
    } else if (this.rank[i] > this.rank[j]) {
      this.parent[j] = i
    } else {
      this.parent[i] = j
      this.rank[j] += 1
    }
  }
}