在一副图中,设a点可达b点,则从a点到b点可能有多条路径,其中距离最小的路径叫做最短路径。对于有负权重环的图,最短路径问题是没有意义的,所以本文提到的有向图都不含负权重环。
对于图中除a外的其他任意可达的点b,最短路径必然存在(当多条路径距离一样,则只取其中一条),所有这些最短路径构成一棵树,叫做最短路径树。所以计算从a点到所有其他可达点的最短路径的过程等价于计算这颗最短路径树的过程。
最短路径树结构:
// PathTree is shortest path treetype PathTree struct {src intdistTo []float64 // 从src到各个可达点的距离edgeTo []int // 到达各个可达点的路径的上一个途经点}
distTo[dst] 记录从 src到dst的最短路径的距离。distTo[src]初始值为0,其余元素的初始值都为正无穷大。
edgeTo[dst] 记录src到dst的最短路径的最后一个途经点,也就是说边(edgeTo[dst] -> dst)就是最短路径的最后一条边,反向追溯即可确定最短路径。
所以计算最短路径树的过程等价于计算 distTo 与 edgeTo 的过程。
边的放松:设有一条 v -> w 的边e,若distTo[w] > distTo[v] + e.weight,则e是有效边,需要把distTo[w]赋值为 distTo[v] + e.weight 以及把 edgeTo[w] 赋值为v。否则e是无效边,不进行任何操作。
点的放松:放松从该点出发的所有边。
命题A: “所有边都满足distTo[w] <= distTo[v] + e.weight(不存在有效边)” 是 “distTo与edgeTo构成一颗最短路径树”的充分必要条件。
证明:
设任意一条最短路径 src —> dst 为 v0->v1->…->vk (v0即src,vk即dst). 若用 ei 表示边 vi-1 -> vi , 边的序列 e1e2ek-1ek 也表示最短路径。
因为所有边都满足distTo[w] <= distTo[v] + e.weight,所以
distTo[vk] <= distTo[vk-1] + ek.weight
distTo[vk-1] <= distTo[vk-2] + ek-1.weight
……
distTo[v1] <= distTo[v0] + e1.weight
distTo[v0] = 0
结合各式可得 distTo[vk] <= distTo[vk-1] + ek.weight <= distTo[vk-2] + ek-1.weight + ek.weight <= ….. <= e1.weight + e2.weight + … + ek-1.weight + ek.weight
因为 e1.weight + e2.weight + … + ek-1.weight + ek.weight 就是最短路径的长度,所以 distTo 记录的就是最短路径的长度
可证是充分条件。
假设存在一条有效边e使得 distTo[w] > distTo[v] + e.weight,则 distTo[w] 可以被赋值为更小的值 distTo[v] + e.weight 且 edgeTo[w] 可以被赋值为v,所以distTo与edgeTo不构成最短路径树,可证条件必要。
计算最短路径树可以归结为:
- distTo[src]设置为0,其余元素的初始值设置为正无穷大
- 放松图中的边直到不存在 可放松的边(有效边)为止
命题B:如果放松过程中确定了最短路径树中的某条路径s,则后续无论如何放松,都不会影响已经确定的路径s。
证明:放松操作只会使路径总距离更短,不可能使路径距离变大,既然已经是最短路径,也无法被放松到更短。
命题C:设有向图有NumVert个顶点,则经过 NumVert-1 轮对所有边以任意顺序放松后,可以得到最短路径树。
证明:
在最短路径树中所有顶点的最短路径,可以根据需要经过边的数量进行划分,这里分别把他们叫做 n边数路径。
经过边数量最少为1,路径形如v0->v1 ,这里称作单边数路径
经过边数量最多为 NumVert-1,形如 v0->v1->….->vNumVert-2->vNumVert-1 ,这里称作 NumVert-1边数路径。
不难证得只需放松点src即可确定最短路径树中的所有 单边数路径。也就是说经过第1轮的所有边放松,可以确定所有单数边路径。
因为所有单边数路径是所有双边数路径的前缀,所以放松所有单边数路径的端点即可确定所有的双边数路径。也就是说经过第2轮的所有边放松,可以确定所有双数边路径。
以此类推,经过第NumVert-1轮的所有边放松,可以确定所有 NumVert-1数边路径。
结合命题B,可证经过第NumVert-1轮的所有边放松,确定了所有的 单数边路径、双数边路径、NumVert-1数边路径,也就是确定了所有的最短路径。
命题C的时间复杂度是 NumEdge*NumVert,十分稳定。本文即将提到的最短路径算法本质上都是在对命题C做优化。
首先把distTo[src]置为0,其他distTo都置为正无穷。
然后放松点src,则src的所有邻接边都会被放松,src的所有邻接点的distTo的值都会变化,这些邻接边实际是单边数路径的超集,而下一轮实际只需要放松单边数路径的端点。无法确定哪些点属于单边数路径的端点,那就把所有distTo变化了的点(实际是src的所有邻接点)都加入队列q。
第2轮放松q中的所有点。distTo变化了的点实际是双边数路径的端点的超集,但是无法分辨,那就把第二轮中distTo变化了的点都加入队列q,用于第3轮的放松。以此类推,最多 NumVert-1 轮放松就可以得到最短路径树。
实现时还可以对队列q中的元素去重,进而减少放松次数,这就是BellmanFord算法,最坏情况复杂度是 NumEdge*NumVert。
BellmanFord在不确定distTo变化了的所有点中哪些点是最短路径的端点的情况下,把所有distTo变化了的点都加入下一轮放松,导致他的复杂度仍然较高。
Dijkstra算法(假设没有负权重边):
- 首先把distTo[src]置为0,其他distTo都置为正无穷。把src加入最短路径树,放松点src。
- 找到未加入最短路径树的所有点中distTo最小的点w
- 放松w,然后重复步骤2,直到所有点都加入最短路径树
顶点0 放松后:
得到两条连接外界的路径:分别是 0->2 到达顶点2,0->4到达顶点4。其中0->2是最小的路径,所以把顶点2以及路径0->2加入最短路径树。可以断定0->2属于最短路径树,因为其他路径到达顶点2只能途径顶点4,而0->4已经大于0->2,且所有边的权重都为正,故而途径4的其他到达2的路径肯定远于路径0->2。
顶点2放松后:
得到两条连接外界的路径:0->2->7到达顶点7,0->4到达顶点4。0->4路径比较近,所以可以断定这条路径属于最短路径树,因为其他到达顶点4的路径必然有前缀0->2->7,而这样的路径必然更远。
顶点4放松后:
得到两条连接外界的路径:0->2->7到达顶点7,0->4->5到达顶点5,(放松边4->7时因为路径0->4->7远于路径0->2->7,所以放松失败)。同理可以断定0->2->7属于最短路径树。
然后放松顶点7,以此类推,得到最短路径树。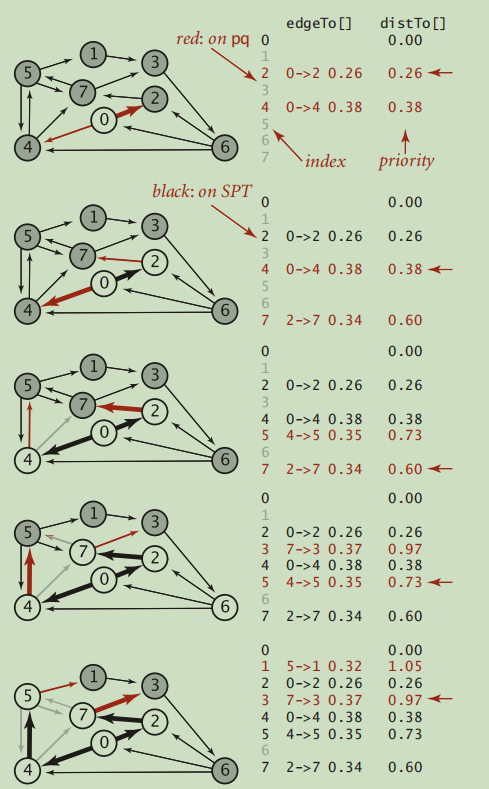
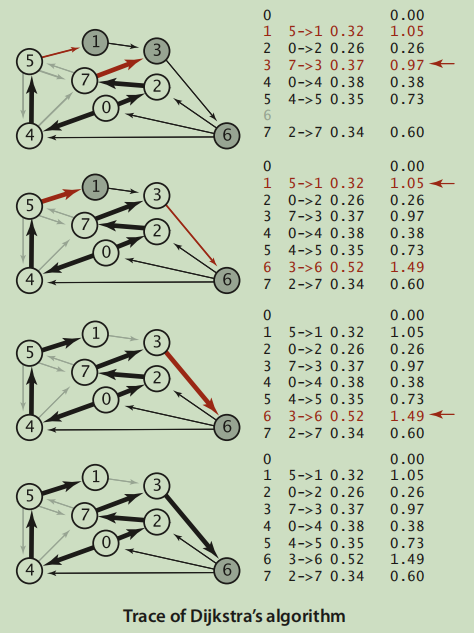
在Dijkstra算法执行过程中,加入最短路径树的点的顺序是以最短路径距离src点的距离从小到大。
实现时用到了优先队列,Pop/Push操作复杂度时 O(lgNumVert),所以整个算法复杂度是 O(NumEdge*lgNumVert)。
计算有向无环图的最短路径树:按照拓扑序放松一遍所有顶点即可得到最短路径树。
证明:因为是按照拓扑序只放松一遍,所以对于任意顶点v,被放松前就已经放松所有指向顶点v的边,且因为只放松一遍,所以distTo[v]不可能再变化,因为e.weight也不可能变化,所以放松过顶点v一次后v的邻接边将不可能变成有效边。所以按照拓扑序放松一遍所有顶点后,所有边都将将满足distTo[w] <= distTo[v] + e.weight,所以就得到了一颗最短路径树。
因为获取拓扑序的复杂度是 O(NumEdge+NumVert),放松过程的复杂度是 O(NumEdge),所以整体复杂度是O(NumEdge+NumVert)。

