以下讨论都基于无向图。

连通图中连接所有顶点的无环连通子图叫做该图的**生成树**
这样的无环子图一定有V-1条边，无环图就是一颗树

一个连通图可以有多颗生成树
所有生成树中，权重之和最小的生成树叫**最小生成树**

切分定理：连通图的任一切分，**横切边**中最小的那一条一定属于最小生成树
证明：
首先，对于连通图的任一切分，所以横切边中至少有一条属于最小生成树，如果一条都没有，那这个最小生成树没把所有顶点连通，就不是一颗最小生成树。
假设最小横切边（m）没有属于最小生成树，那么就一定有一个非最小的横切边（f）属于最小生成树。此时往生成树中加入边m，去掉边f，得到的仍然是生成树，且是更小的生成树，所以之前的不是最小生成树，所以得证最小横切边一定属于最小生成树。

当图中所有边的权重是唯一的，则最小生成树也是唯一的
证明一：
将图中所有边按权重从小到大排序，一个一个拿出来，若拿出的边e

不与之前已经拿出的边形成环，则e必然属于切分（e的一端已经拿出的边所形成的树的所有顶点与其他顶点的切分）的最小横切边，即e必然属于最小生成树。
与之前已经拿出的边形成环，则不属于任何切分的最小横切边，因为切过该边的划分必然也切过该环中其他的某一条边，其他的边比他先拿出来即都比他小。

当共得到V-1条边时即确定了最小生成树。如此下来，只能得到一个唯一的最小生成树。

注意：
这里也证明了，当各边权重不唯一时，那么在给边排序时，权重相同的边的顺序是不确定的，则最后得到的最小生成树也可能是不唯一的

证明二：

假设它存在两颗最小生成树a, b 我们找到这两个方案不同的边中最小的一条边x, (既x在一个生成树上，不在另一个生成树上)。假设x在a里面，那我们考虑把x塞到b里面去，这样b+x里面肯定有一个环，环上至少有一条边比x大（如果每条边都比x小，那根据x的定义这些边肯定也都在a里面，那a就有环了，矛盾），把这条边去掉之后还是一个生成树（你考虑把环去掉一条边变成了链，但是原来联通的现在也还是联通的）。但是这颗生成树比b小（加进了一条x，去掉了一条比x大的边），所以b不是最小生成树，矛盾故最小生成树是唯一的

https://www.zhihu.com/question/43504951/answer/95831183

Prim

找到最小生成树，即找到最小生成树的所有边

lazy version

找到任一顶点，加入集合s，据切分定理集合s与其他所有顶点的划分可以确定最小生成树的一条边，确定一条边后将该边另一头的顶点加入集合s，集合s与剩余顶点的划分又可以确定一条属于最小生成树的边。重复这个过程，一共V-1个划分会得到所有V-1条属于最小生成树的边。

问题是怎么确定每个划分有哪些横切边？并怎么找出最小横切边？

集合s与其他顶点的划分的所有横切边，即集合s与跟集合s相邻的顶点之间的边，即集合s中的所有顶点的边的并集除去集合s内部的边
实现的时候用marked []bool标记是否属于集合s，用一个优先队列保存集合s与其他顶点的划分的所有横切边。每次新加入顶点v时，将marked[v]标记为true，将v.Adjacent()返回的边中另一头顶点不属于集合s的边加入优先队列中。
但是这个实现随着算法进行，优先队列中会出现集合s内部的边（因为集合s不断扩大，之前它不是内部边，后来是了），所以获取最小横切边时要判断优先队列DelMin()得到的是不是内部边。下图中新加入顶点2后优先队列中出现灰色的边，灰色的边即变成了内部的边，即失效的边。除灰色的边外都是集合s与其他顶点的划分的横切边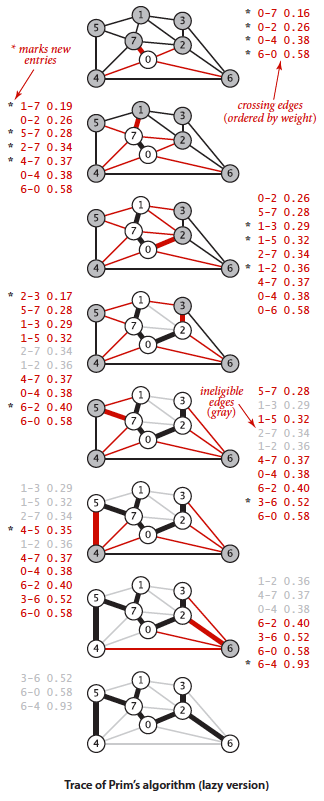

lazy version分析：
空间复杂度为E（边总数），因为最坏情况下优先队列保存所有边，数组marked大小为V（顶点总数）
时间复杂度为ElgE，因为优先队列最坏情况有E条边，一次Insert或DelMin操作为lgE，操作次数与E成正比

即时版本

lazy version的优先队列中会存有内部边（失效的边），即时版本就是能保证优先队列里面不会产生内部边。

优先队列中产生内部边的原因：
观察图中第4副发现加入顶点2开始出现内部边（灰色），观察图中第3副发现之所以这时候出现内部边是因为第3副中连接顶点2的边有3条，当弹出最小的一条并加入顶点2则另外2条边就变成内部边。

所以保证连接每一个邻居顶点的边唯一即可，且这个边应该是连接这个邻居顶点的所有边中最小的那条。

所以实现中在往优先队列中加入v.Adjacent()时，不加入内部边，还要保证：当考虑是否加入边v-w时，若之前不存在集合s到w的边则加入，若已经存在集合s到w的边则将其修改为这两条边中较小者。

找到连通图的最小生成树：
edgeTo保存树到某个邻点的最小边，是点到唯一最小边的映射
pq只保存树的所有邻点以及到该邻点的最小距离（权重），以获得树的所有邻点中的最近点，再借助edgeTo获得树的所有邻边的最小边
为什么要弄个映射，不直接在pq中存到各个邻点的最小边呢？如果pq存的元素是[到邻点的最小边:该边的权重]，当到某个邻点（w）的最小边要更新，需要更新pq中通往w的边，即要读出pq中所有边并找到通往w的边（e），然后pq.Delete(e, e.p);pq.Insert(smallerEdge, smallerEdge.p)。然而若pq存的元素是[邻点:到该点的最小距离],就直接pq.Update(w, smallerEdge.p);edgeTo[w] = smallerEdge

func prim(g EdgeWeightedGraph, v int, marked []bool, edgeTo []*Edge) *queue.LinkedQueue {
    pq := pqueue.NewBinHeap(g.NumV() - 1)
    marked[v] = true
    adj := g.Adjacent(v) // 获取任一顶点的所有邻边
    for _, e := range adj {
        w := e.Another(v)
        pq.Insert(e.weight, w) // 将每个邻边的权重、邻居顶点 加入pq
        edgeTo[w] = e // 邻边的实例存到数组中，即邻点到邻边映射的符号表
    }
    mst := queue.NewLinkedQueue()
    for !pq.IsEmpty() {
        m := pq.DelMin()
        w := m.(int) // 获取整个树的最小邻边所到的点（称它为最近点吧）
        mst.PushBack(edgeTo[w]) // 借助映射获取整个树的最小邻边，即一条属于mst的边
        primVisit(g, w, marked, pq, edgeTo) // 把最近点的邻边加入edgeTo和pq
    }
    return mst
}
func primVisit(g EdgeWeightedGraph, v int, marked []bool, pq *pqueue.BinHeap, edgeTo []*Edge) {
    marked[v] = true
    adj := g.Adjacent(v)
    for _, e := range adj {
        w := e.Another(v)
        if marked[w] { // 跳过内部边
            continue
        }
        if edgeTo[w] == nil {
            pq.Insert(e.weight, w)
            edgeTo[w] = e
        }else if e.weight < edgeTo[w].weight {
            pq.Update(e.weight, w)
            edgeTo[w] = e
        }
    }
}

Kruskal

将图中所有边按权重从小到大排序，一个一个拿出来，若拿出的边e

不与之前已经拿出的边形成环，则e必然属于切分（e的一端已经拿出的边所形成的树的所有顶点与其他顶点的切分）的最小横切边，即e必然属于最小生成树。
与之前已经拿出的边形成环，则不属于任何切分的最小横切边，因为切过该边的划分必然也切过该环中其他的某一条边，其他的边比他先拿出来即都比他小。

当共得到V-1条边时即确定了最小生成树。

怎么知道拿出的边会不会和之前的边形成环？在尚未拿出任一条边时，把所有顶点看作孤立的，拿出一条边会使顶点连接起来形成树（因为会使其形成环的边被忽略了）。如果拿出的边的两边顶点属于同一颗树，则相当于往一棵树中加一条边，就会形成环，否则就不会形成环。那么可以把属于同一颗树的顶点看作一个集合，问题等同于判定两个点是否属于同一个集合，就想到了Union-Find算法。

数据结构与算法

无向图的最小生成树

Prim

lazy version

即时版本

Kruskal