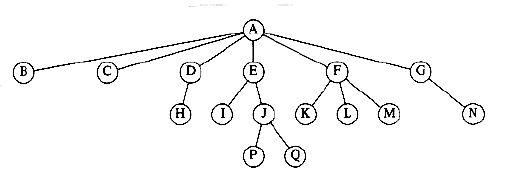
树

逻辑结构

实现

应用

文件系统

二叉树

定义

任意节点的孩子不超过两个的树

逻辑结构&实现

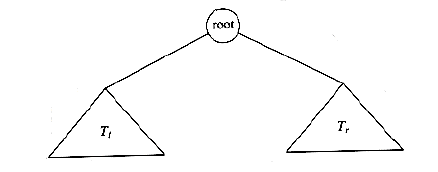
typedef struct tree_node *tree_ptr;
struct tree_node
{
    element_type element;
    tree_ptr left;
    tree_ptr right;
};
typedef tree_ptr TREE;

应用

表达式树
后缀表达式—>表达式树—>前缀/中缀表达式

二叉查找树

定义

任意节点满足左子节点<该节点<右子节点的二叉树

实现

Find

func (n *node) find(key int) *node {
    if n == nil {
        return nil
    }
    if key < n.key {
        return n.leftSon.find(key)
    }
    if key > n.key {
        return n.rightSon.find(key)
    }
    return n
}

查找树为空的时候，返回nil
要找的节点与当前根节点相等时，返回当前根节点。不相等时，向左或向右递归查找。

FindMin

迭代找到最左节点

func (n *node) findMin() *node {
    if n == nil {
        return nil
    }
    for n.leftSon != nil {
        n = n.leftSon
    }
    return n
}

FindMax

迭代找到最右节点

func (n *node) findMax() *node {
    if n == nil {
        return nil
    }
    for n.rightSon != nil {
        n = n.rightSon
    }
    return n
}

Insert

我一开始是这样想的：
往一颗树里面插入一个节点，往根节点的子节点插入即可，那么不需要返回值。插入一个新节点则需要使父节点的指针指向它，所以insert需要传父节点的指针，父节点有两个指针所以还要传一个变量提示应该修改父节点的左儿子还是右儿子。这样一来函数里面要判断父节点为不为nil，判断应该修改父节点左儿子还是右儿子。这样还是有个痛点，树一开始为空的时候，插入一个节点却无法修改函数外层的nil指针。这个思路延续到了删除操作。最后花几个小时实现通过测试，十分复杂。

插入操作后返回一颗新树，外层insert更新它的左子树或者右子树！一切都简单了

func (n *node) insert(k int, v interface{}) *node {
    if n == nil {
        n = new(node)
        n.key = k
        n.value = v
        return n
    }
    if k < n.key {
        n.leftSon = n.leftSon.insert(k, v)
        return n
    }
    if k > n.key {
        n.rightSon = n.rightSon.insert(k, v)
        return n
    }
    n.value = v
    return n
}

Delete

删除操作需要修改被删除节点的父节点的指针，所以要返回希望父节点更新成的指针

删除叶子：直接返回nil
删除节点有一个儿子：返回儿子节点
删除节点有两个儿子：
1. 查找左子树的最大节点或者右子树最小节点x
2. 把删除节点替换为x
3. 删除x，注意x一定只有一个儿子

func (n *node) delete(key int) *node {
    if n == nil {
        fmt.Printf("avltree: delete not existed key(%v)", key)
        return nil
    }
    if key < n.key {
        n.leftSon = n.leftSon.delete(key)
        return n
    }
    if key > n.key {
        n.rightSon = n.rightSon.delete(key)
        return n
    }

    if n.leftSon == nil {
        return n.rightSon
    }
    if n.rightSon == nil {
        return n.leftSon
    }
    deleted := n
    // to make it randomly
    if time.Now().UnixNano()&1 == 1 {
        n = n.leftSon.findMax()
        n.leftSon = deleted.leftSon.delete(n.key)
        n.rightSon = deleted.rightSon
    } else {
        n = n.rightSon.findMin()
        n.rightSon = deleted.rightSon.delete(n.key)
        n.leftSon = deleted.leftSon
    }
    return n
}

分析

当输入序列随机生成，它是平衡的，以上所有操作都是lgN
但是当输入有序时，就会变得十分不平衡，甚至成为一个链表

应用

符号表

AVL树

二叉查找树简单，但是它可能出现不平衡，我们需要一种平衡的树

任意节点的左右子树的高度差不超过1的二叉查找树就叫平衡二叉树（AVL树）。

实现

type node struct {
    key   int
    value interface{}

    height   int8 // height不能用uint，uint做减法运算时容易发生下溢出
    leftSon  *node
    rightSon *node
}

Find、FindMin、FindMax 操作同普通二叉查找树

rotation

首先，应该介绍二叉查找树通用的旋转操作，此操作之后不破坏二叉查找树的性质：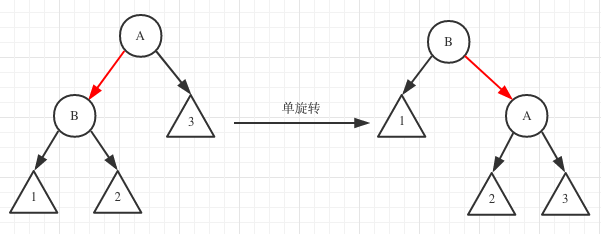

一次单旋转的操作对象就是红链接两边的节点。把A的左指针改指向2子树，B的右指针改指向A。然后依次调整A、B的height项。
当然，图右也可以对称的转为图左，也叫单旋转。

Insert

AVL的insert是跟普通二叉查找树的insert类似，不过要在递归回溯的时候调整height项，且当两子树差值大于1（即2）时使树回归平衡

回溯的过程是从插入的位置回溯到根节点为止。事实上只需要进行一次平衡调整，因为一次平衡调整后返回的新树高度并没有增加

首先假设回溯路径中需要调整的节点为A，则A的左右子树当中其一高度为h，另一个高度为h+2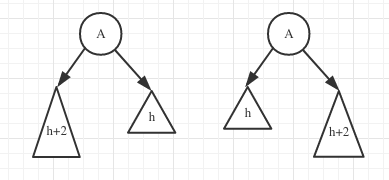

高度为h+2的子树的左右子树当中必定其一高度为h+1，另一个呢？一定是h！
因为这里假设的前提是： 1.插入前树是平衡的 2.A是发生不平衡的点
如果它大于h，则违背前提1
如果它小于h，则违背前提2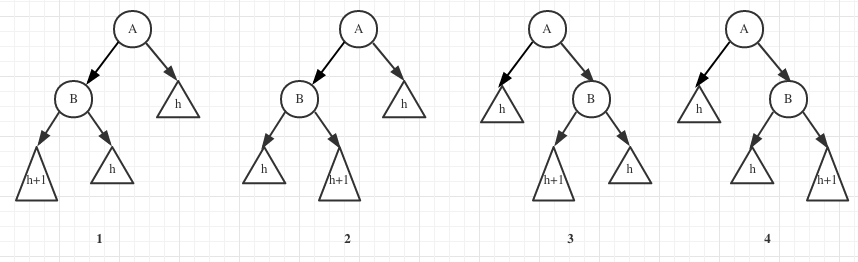

插入后只有这四种情况。

对情况1、4执行一次单旋转，得到的新树满足平衡（且高度没有增加）。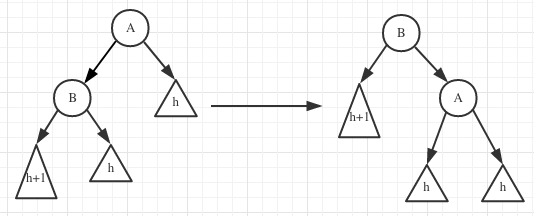

对于情况2、3，可以对h+1子树继续分解。分解得到子树其一高度一定为h-1（h>=1）
执行一次双旋转（其实就是两次单旋转）后得到的新树满足平衡（且高度没有增加）。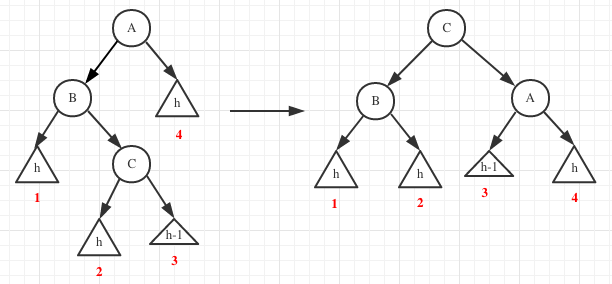

Delete

AVL的delete是跟普通二叉查找树的delete类似，不过要在递归回溯的时候调整height项，且当两子树差值大于1（即2）时使树回归平衡

分析

各项操作均为lgN的平衡二叉查找树

2-3树

又叫3阶B树
是为了给红黑树做铺垫

树中任意节点为2-节点（1个key）或者3-节点（2个key），且空链接到根节点的距离相等（空链接在同一水平线上）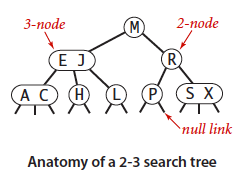

实现

Find与二叉查找树相似

Insert

前面就是一个查找操作，后面有三种情况：

找到了。直接更新value
没找到，最后到达的叶子节点是个2-节点。直接往2-节点插入变成3-节点
没找到，最后到达的叶子节点是个3-节点。插入使3-节点变成4-节点，需要消除4-节点。设4-节点的key分别叫k1,k2,k3。让4-节点的k2脱离出来成为父节点的最小key，然后k2的两边链接分别指向k1，k3 .如果这使得父节点变成4-节点了，则递归回溯的时候以同样方式消除4-节点。

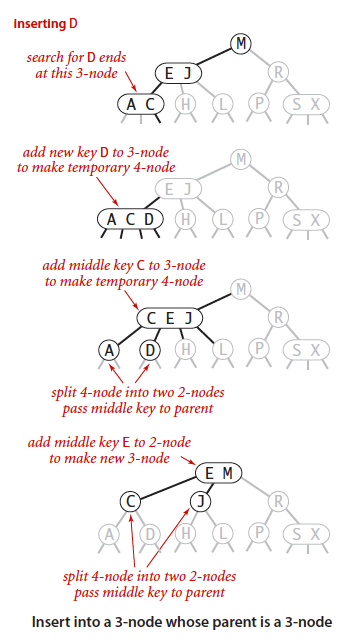
容易想到，2-3树是向上生长的，所以它能保证下面的空链接始终在同一水平线上。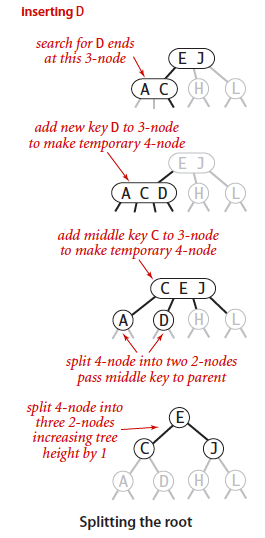

DelMin

删除最小key，若最小key位于一个2-节点则会破坏性质所有空链接在同一水平线上。于是删除最小key前，要通过调整保证它位于一个至少3-节点（整颗树只有一个节点除外）。

从根节点开始，删除树中的最小key
左儿子为nil，当前key即最小key，直接删除
左儿子不为nil，但是一个2-节点。若右儿子是3-节点，则右儿子送一个key给左儿子。否则只能父节点的最小key与两个儿子结合成一个4-节点（消除4-节点的逆过程）。