Day9.1 剑指 Offer 42. 连续子数组的最大和

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。

看时间要求 就是要一次遍历就完事

看了 大佬们一次遍历的方法 — 使用动态规划
大概思路如下：

  • 建立一个dp数组，存放连续数组num[i]处对应的最大值dp[i] (只是这一段上比较大的值 不是整体最大的值)
  • 数组的变化情况有两种状态
    • 如果dp[i-1] 是 负数，则num[i] 加上它就会变小 ，不如自成一个子序列，dp[i] 就是它自己
    • 如果dp[i-1] 是正数，则num[i] 加上它就会变大，dp[i] 当然是加上前面的值

      方法1：dp数组

      所以动态方程就是：python
      dp[i] = dp[ i-1 ] + num[i] if dp[i-1] >0 else: num[i]
  1. class Solution:
  2.     def maxSubArray(self, nums: List[int]) -> int:
  3.         dp = [0]*len(nums)
  4.         dp[0] = nums[0]
  6.         for i in range(1,len(nums)):
  7.             if dp[i-1] > 0:
  8.                 dp[i] = dp[i-1] +  nums[i]
  9.             else:
  10.                 dp[i] = nums[i]
  12.         return max(dp)

这里由于dp 数组的存在 空间复杂度为 O(N)
而且dp数组寻找最大值输出，使得时间复杂度为 2n
执行用时：48 ms, 在所有 Python3 提交中击败了94.22%的用户
内存消耗：20.8 MB, 在所有 Python3 提交中击败了28.41%的用户

优化：变量换数组

这里用两个变量做优化

  • 一个变量 存储 dp[i-1]
  • 一个变量 存储当前最大值

最后返回最大值即可

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        dp_pre = nums[0]
        dp_max = nums[0]

        for num in nums[1:]:
            if dp_pre > 0:
                dp_pre = dp_pre + num
            else:
                dp_pre = num

            dp_max = dp_pre if dp_pre > dp_max else dp_max

        return dp_max

执行用时：40 ms, 在所有 Python3 提交中击败了99.19%的用户
内存消耗：18.5 MB, 在所有 Python3 提交中击败了69.63%的用户

理论上已经很好了。。就介样ba

Day9.2 剑指 Offer 47. 礼物的最大价值

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

woc 这不是找一条最优路径吗这不是
这不是强化学习吗 这不是

如果从左上角就选最好的(贪心)，最后走到终点不一定是最好的【可能会被局部最优引走】

但是如果从终点往回走，确定后面的是最好的，往回倒走一步，哎 这一步也选最好的 就能保证是最好的【是这样吗】

想挺美 但是不太会写 — 看看人家 说的好清晰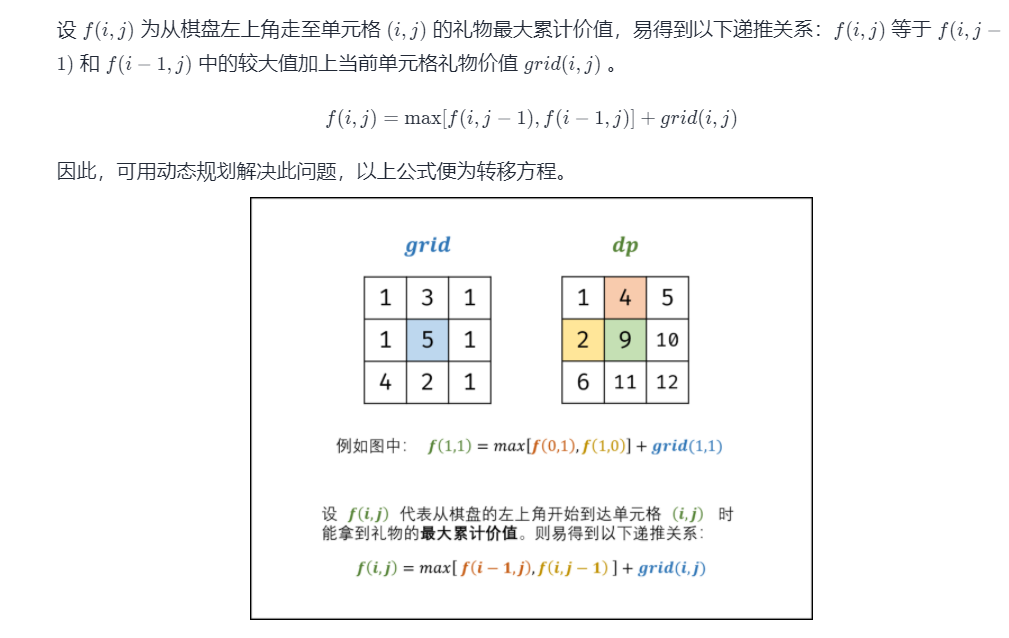
image.png
这样计算当前最优值的时候 就要把后面的最优值都计算出来 — 就是相当于倒着往回走
这样 是不是要递归向下 — 应该是

边界条件 — 触达 mn 的边界