剑指offer31天 第 8 天 动态规划（简单）

来来来！！ 让我杀个痛快！！！

Day8.1 剑指 Offer 10- I. 斐波那契数列

输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）

三步优化 —- 因为本质就是暴力解法 主要在辅助空间内存做优化

方案1：直接递归

就 用动力公式(从旧状态进入到新状态，也可以叫贝尔曼方程) 直接干！

class Solution:
    def fib(self, n: int) -> int:
        if n == 1 or n == 2:
            return 1
        return self.fib(n-1) + self.fib(n-2)

运行直接报错：递归占用空间太大了 递归深度很深 具体是多少呢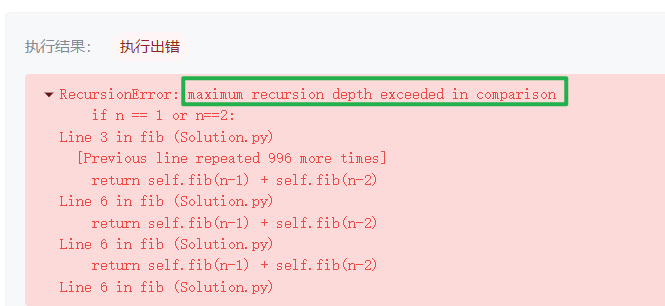

这个
时间复杂度：2n吧 每次有两套N要计算
空间复杂度：？
反正有很多的重复计算
字节面试要求写出logn解法

优化1：建立查询表

因为两边子树计算的时候有大量的重复计算的元素，所以建立一个表去做查，

• 如果没计算过就添加到表
• 如果计算过就把表上的元素值返回 — 避免重复计算

构建表也有两种方式，

• 一种是从下往上构建：0—n
• 一种是从上往下构建：n—0

1）从上往下构建：n—0
利用哈希表
时间：N
空间：N

class Solution:
    def fib(self, n: int) -> int:
        table_n = {0:0,1:1}

        return self.recur(n,table_n)

    def recur(self,N,table):

        if N in table.keys():
            return table[N]
        else:
            table[N] = (self.recur(N-1,table) + self.recur(N-2,table) ) 
            if table[N] < 1000000007:
                return table[N]
            else: 
                return table[N] % 1000000007

执行用时：36 ms, 在所有 Python3 提交中击败了40.29%的用户
内存消耗：15 MB, 在所有 Python3 提交中击败了32.41%的用户

2） 从下往上构建：0—n

从底向上构建，就是一个迭代过程了
时间：N
空间：N
但是代码简洁了许多

class Solution:
    def fib(self, n: int) -> int:

        if n < 2:
            return n

        table_n = [0] * (n+1)
        table_n[1] = 1
        table_n[2] = 1

        for i in range(3,n+1):
            table_n[i] = table_n[i-1] + table_n[i-2]

        return table_n[n] % 1000000007

优化2：将表压缩成两个值

其实最终的结果只和 前面两个值有关
可以把空间为N的表 优化成 O(1)

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0
        if n == 1 or n == 2:
            return 1
        pre_1 = 1
        pre_2 = 1

        for _ in range(3,n+1):
            cur = pre_1 + pre_2
            pre_2 = pre_1
            pre_1 = cur

        return cur % 1000000007

Day8.2 剑指 Offer 10- II. 青蛙跳台阶问题

一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法

最优子结构问题

• n= 1 时 就一种
• n= 2 时 (1,1)，2两种
• n= 3时，(1,1,1), (1,2),(2,1)三种

然后不会了 — 感觉和凑零钱是一个问题 相当于只有 1 2 两种面额的零钱

看答案前再想一步： 考虑这是一个DP问题，那这个动力方程 — 下个状态和当前状态的关系
St+1 = St+ 1 + St-1+1 【如果这个成立 那不就是斐波那契数列加2吗】

不对 不能+1 因为最后跳1 还是2 ，整体就是一种方法
所以应该和斐波那契数列一样 【只是从1开始而已】
St+1 = St + St-1

• 即：假如知道了 n-1 有多少种跳法 — n 就是在此基础上加一种即可【不行 还要考虑最后跳2阶的一种可能】

问题：触底问题

• 触底应该列举到 1，还是2

• 最小可能满足的跳法如何描述

  Ok battal到这里，应该已经有答案了
  直接用斐波那契数列最优的方法做

class Solution:
    def numWays(self, n: int) -> int:
        if n ==1 or n==0 :
             return 1
        if n ==2:
            return 2

        pre_1 = 2
        pre_2 = 1
        cur = pre_1 + pre_2
        for _ in range(3,n+1):
            cur = pre_1 + pre_2
            pre_2 = pre_1
            pre_1 = cur

        return cur % 1000000007

和斐波那契数列基本一致 就是最后面的几个元素干掉了几个

用python的用法特点，稍稍优化一点点

class Solution:
    def numWays(self, n: int) -> int:
        if n ==1 or n==0 :
             return 1
        if n ==2:
            return 2

        pre_1 = 2
        pre_2 = 1
        for _ in range(3,n+1):
            pre_1,pre_2 = pre_1 + pre_2,pre_1

        return pre_1 % 1000000007

Day8.3 剑指 Offer 63. 股票的最大利润

把某股票的价格按照时间先后顺序存储在数组中，
请问买卖该股票一次可能获得的最大利润是多少？

找到一个数组中的一个幅度变化最大的一段距离

这个题应该不是第一次做了
直观思路就是，记录一个初始比较小的值，然后用迭代后面的值查看最大的落差

• 每次判断两件事
  • 1. 是不是比最小值还小
  • 1. 是不是区间值很大

不行啊，，，感觉逻辑不通顺

看题解大佬

• 这个大佬的方法展示一下， dp 很清晰

简化一下 不用表 就用俩值

• 一个记录最大利润
• 一个记录最小的价格

show code !!!

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        min_prices = int(1e9)
        max_profit = 0 # 如果一直是负的就是 0 不买卖了

        for day_pri in prices:
            if day_pri < min_prices:
                min_prices = day_pri
            max_profit = max(max_profit,day_pri - min_prices)

        return max_profit

优化一点点：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        min_prices = int(1e9)
        max_profit = 0 # 如果一直是负的就是 0 不买卖了

        for day_pri in prices:
            min_prices = min(min_prices,day_pri)
            max_profit = max(max_profit,day_pri - min_prices)

        return max_profit