这个需求是在绘制地图过程中，通过经纬度边界绘制地图的点阵。有这么几个方法：

• 射线法：从判断点向某个统一方向作射线，依交点个数的奇偶判断；
• 转角法：按照多边形顶点逆时针顺序，根据顶点和判断点连线的方向正负（设定角度逆时针为正）求和判断；
• 夹角和法：求判断点与所有边的夹角和，等于360度则在多边形内部。
• 面积和法：求判断点与多边形边组成的三角形面积和，等于多边形面积则点在多边形内部。

比较下来面积计算比较复杂，角度计算开销比较大，射线法也要对每个边进行求交运算，但总体来说还是比其它方法好一些，下面就是最常用的射线法。

射线法

方法是从验证点向任意方向引一条射线，与多边形相交。计算射线与多边形的边的交点个数。

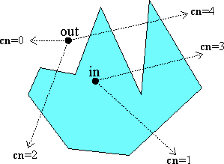
交点个数为奇数，则判断点在多边形内；偶数，则在多边形外。
但是，有这样的特殊情况：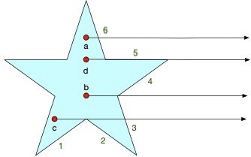

因此定义了以下规则：

• 射线与多边形的边重叠不计。
• 相交点是边的上端点时不计。

这时：
a：与边6一个交点
b：与边4一个交点，与边3交点不计。
c：与边1、2交点不计，与边3一个交点。
d：与边4交点不计，与边5平行不计，与边6一个交点。

那么下面说说代码实现：（由于我获取的地理边界是PHP接口，下面用PHP说明，当然，翻译成别的语言也很容易）

/*
 *    @pt
 *    @polys
*/
function PointInPoly($pt, $polys) {
  $c = 0; //
  $l = count($polys); //
  $p1 = $polys[0];
  for ($i = 1; $i <= $l; $i++) {
    $p2 = $polys[$i]; // p1p2
    if ($pt[0] > min([$p1[0], $p2[0]]) 
        && $pt[0] <= max([$p1[0], $p2[0]]) 
      && $pt[1] <= max([$p1[1], $p2[1]]) 
        && $p1[0] != $p2[0]) {
            if ($p1[1] == $p2[1]) {
                $c++;
            } else {
                $x = ($pt[0] - $p1[0]) * ($p2[1] - $p1[1]) / ($p2[0] - $p1[0]) + $p1[1];
                if ($pt[1] <= $x) {
                $c++;
            }
        }
    }
    $p1 = $p2;
  }
  return $c % 2 != 0;
}