摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。
例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。
示例 1:

• 输入: [1,7,4,9,2,5]
• 输出: 6
• 解释: 整个序列均为摆动序列。

本题通过删除一些元素使得剩下的元素符合摆动序列的要求,到底应该删除哪些元素呢?

首先看一个例子帮助我们理解:
[ 1 ,17,5,10,13,15,10,5,16,8]
观察该序列的前六位: 1,17,5,10,13,15 橙色部分为上升段
其中他有三个子序列为摇摆序列
分别是 1,17,5,10
1,17,5,13
1,17,5,15
只看前六位,要满足是摇摆子序列的要求,就需要在10,13,15中选出一个数,删除两个数,使得前六位中剩下的四个数构成摇摆序列.那么根据经验我们会选择最大的那个.原因:使得下一个元素和选中的元素落差更大,让摇摆子序列的长度增加

所以我们选取的元素应该是 每次状态发生转换的地方,即红色标识的地方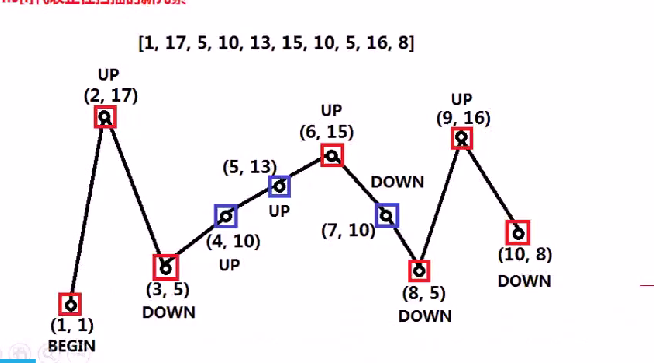

所以我们可以设置三个状态,分别是begin,up,down.当状态发生转换的时候,lengt++

贪心的思想:
局部最优: 删除单调坡度上的节点(不包括单调坡度两端的节点),使得一个坡度就可以拥有两个局部峰值(最大值和最小值)
整体最优: 整个序列拥有最多的局部峰值,从而达到摆动序列最长的目的

附上代码:

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        if(nums.size()<2)
        return nums.size();
       //begin=0,up=1.down=2;
       int tag=0;
       int  x=1;
       for(int i=0;i<nums.size()-1;i++)
       {
           switch(tag)
           {
               case 0:
               if(nums[i]>nums[i+1])
               {
                   x++;
                   tag=2;
               }
               else if(nums[i]<nums[i+1])
               {
                   x++;
                   tag=1;
               }
               else if(nums[i]==nums[i+1]) //这里要把相等单拎出来,因为测试样例中有[0,0,0]的情况
               tag=0;
               break;
               case 1:
               if(nums[i]>nums[i+1])
              {
                   x++;
                 tag=2;
              }
               break;
               case 2:
               if(nums[i]<nums[i+1])
              {
                   x++;
                 tag=1;
              }
               break;
           }
       }
       return x;
    }
};