编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

方法一：一次二分查找

由题目我们可以得出：如果把二维数组看成一维数组，那么他的元素是单调递增的。所以就可以让左指针指向一维数组的开始，右指针指向一维数组的结尾，那么mid=(r+l)/2;在一维数组中下标为mid的元素，放在二维数组当中就是[mid/n][mid%n]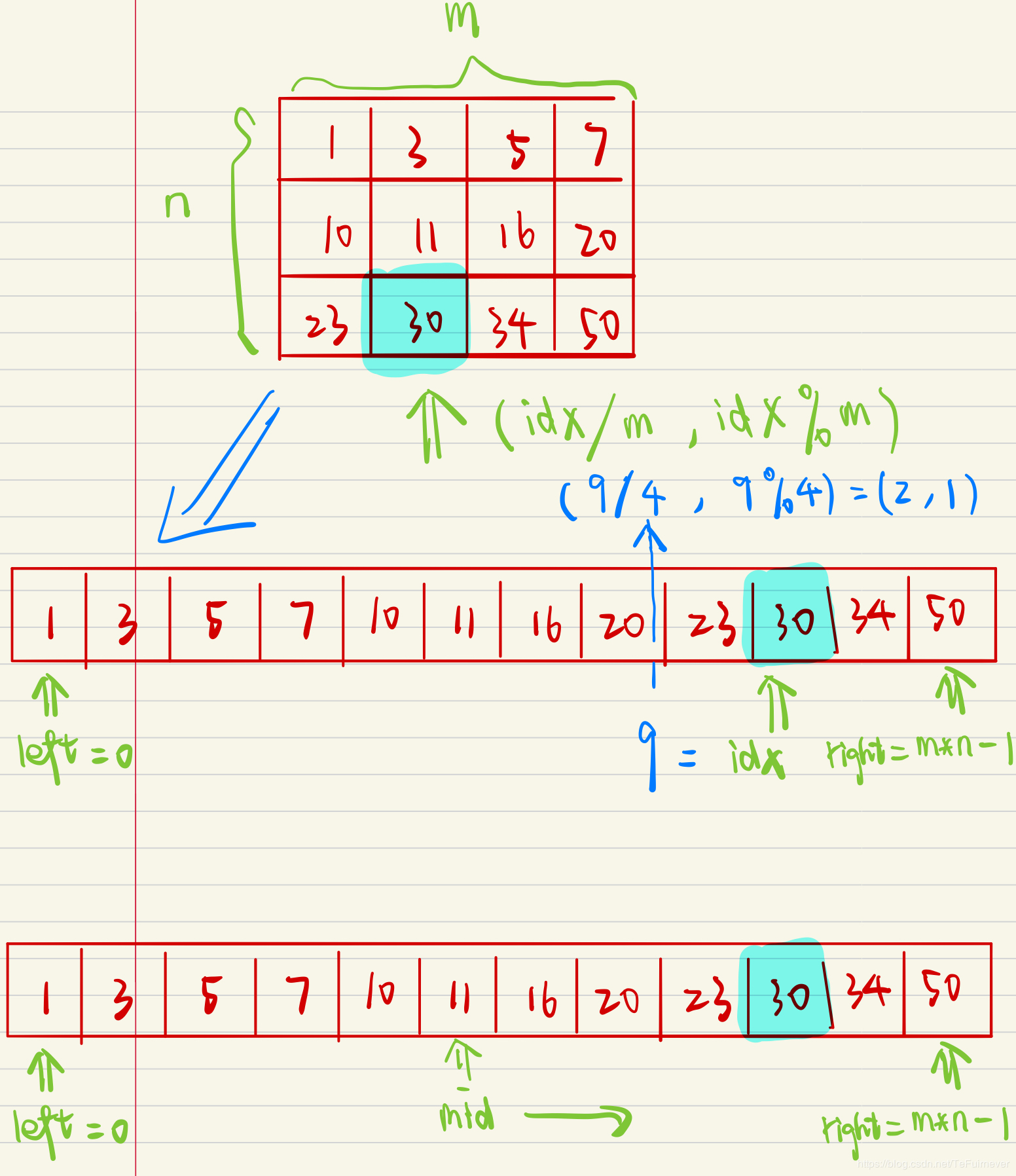
image.png
下附代码：

  1. class Solution {
  2. public:
  3.     bool searchMatrix(vector<vector<int>>& matrix, int target) {
  4.       int m=matrix.size();//行数
  5.       int n=matrix[0].size();//列数
  6.       int l=0,r=m*n-1;
  7.       while(l<=r)
  8.       {
  9.           int mid=(r-l)/2+l;
  10.           int num=matrix[mid/n][mid%n];
  11.           if(num==target)
  12.           return true;
  13.           else if(num<target)
  14.           l=mid+1;
  15.           else 
  16.           r=mid-1;
  17.       }
  18.       return false;
  19.     }
  20. };

方法二：两次二分查找

先对每一行的第一个元素进行二分查找，找到最后一个小于等于target的的那一行，然后在那一行里查找。

但是我不太会第一次查找…….