思路

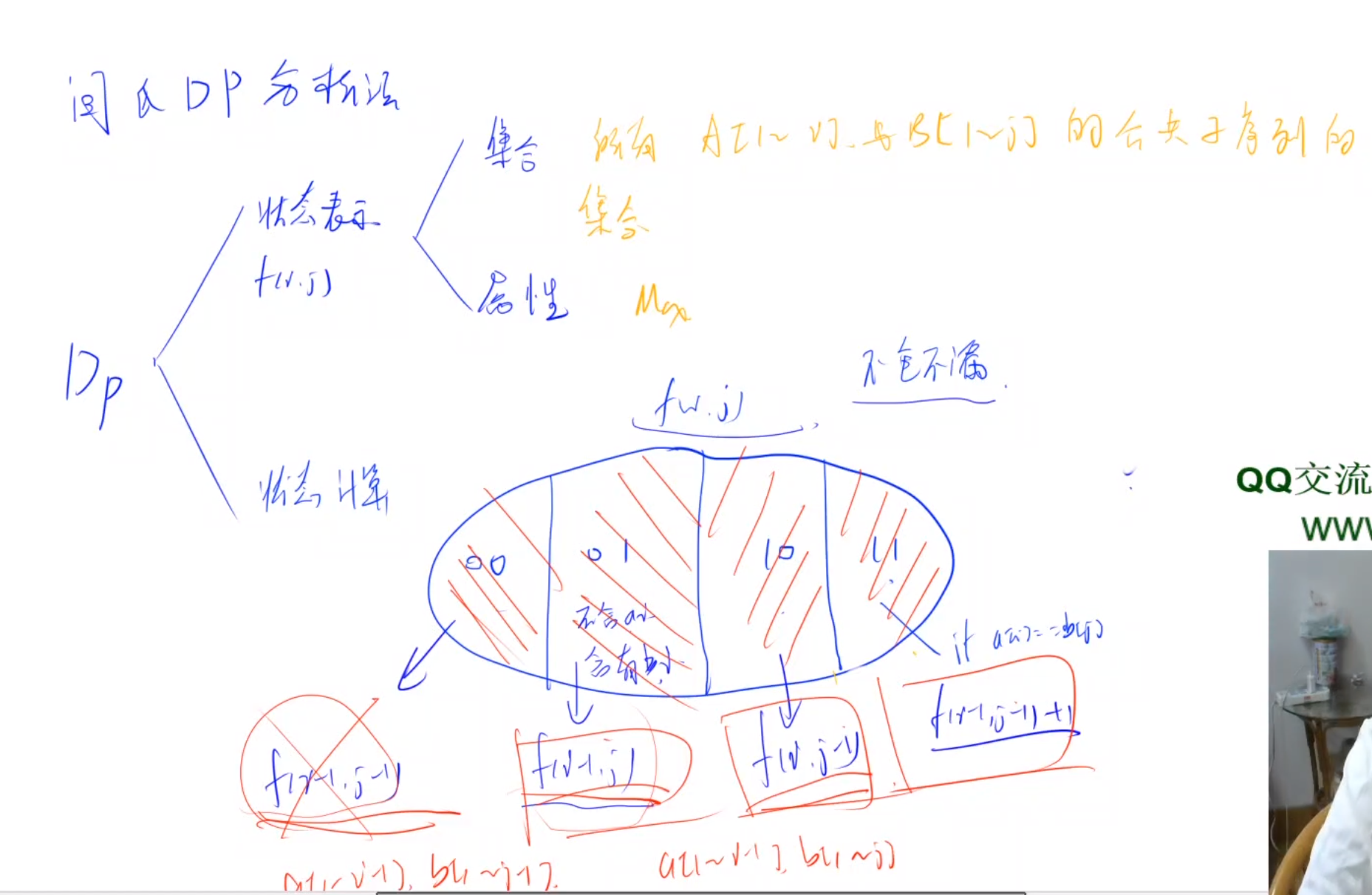
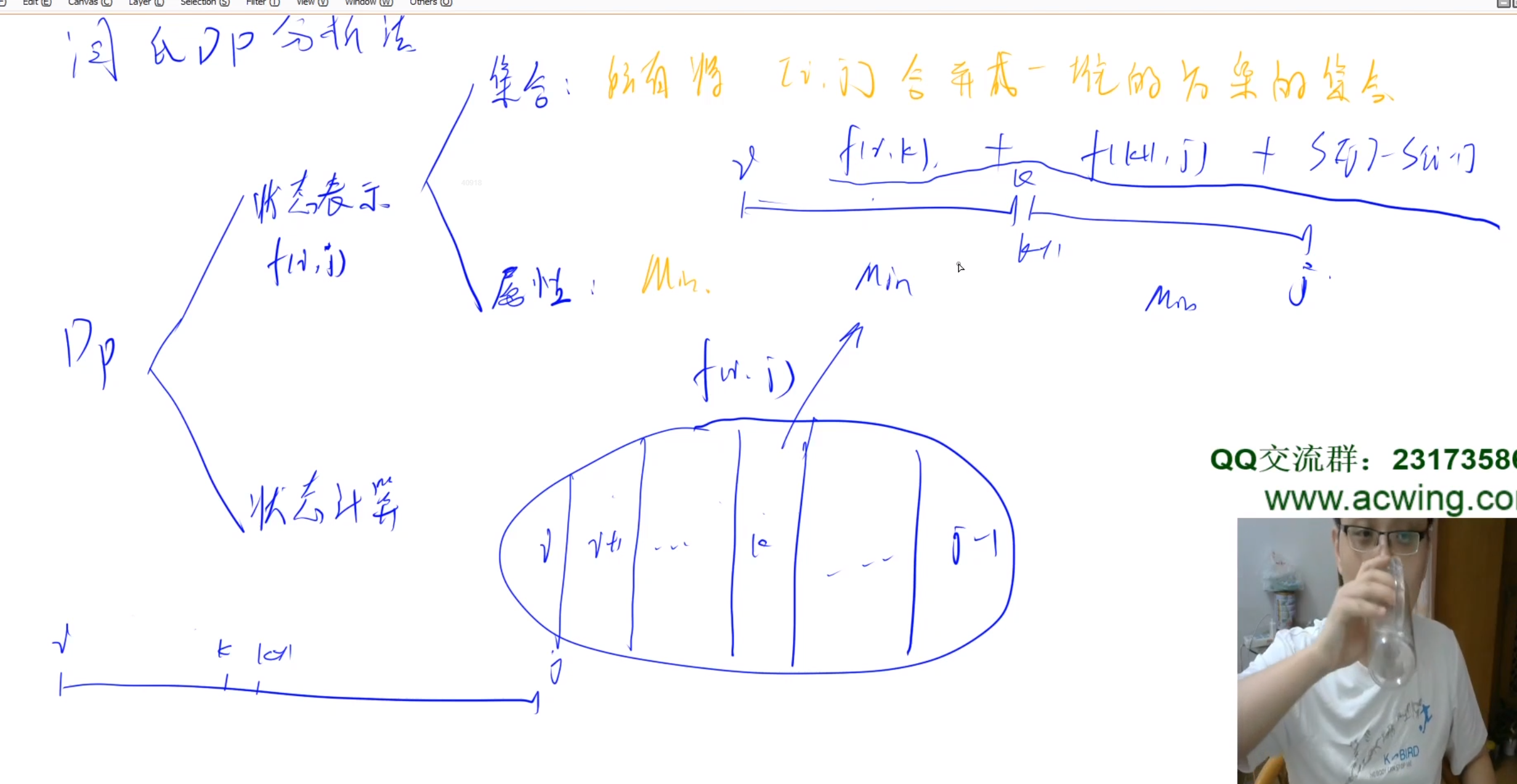
  • 首先是状态表示，怎么才能用变量表示最终的结果和中间的演化过程。状态表示这个里面分为两个部分，第一个是集合，由于DP其实是穷举法的优化，所以你的状态表示了某一类题解/集合。第二个是要求这个集合的某个属性，即属性值，比如最大值，最小值，数量等。
  • 然后是状态转换，如何用之前的某几个集合表示新的集合。通常简单的方式是集合分割，把集合分成几个部分，分别求出对应集合的属性值，然后再求出新状态的属性值。

image.png

0-1背包问题

  • 集合：f(i, j)表示前i件物品，体积不超过j的所有题解
  • 属性值：价值的最大值
  • 状态划分：是否包含第i个物品

  • 状态转换：f(i, j) = max{ f(i - 1, j), f(i - 1, j - v_i) + w_i }

  • 另外多说一句，0-1背包问题优化为1维的，但实际上是对二维做了等价变换，相当于在一维数组内存了i的状态和i-1的状态，并巧妙的利用更新顺序，达到了二维的目的。

    完全背包问题

  • 集合：f(i, j)表示使用前i件物品，体积不超过j的所有题解

  • 属性值：价值的最大值
  • 状态划分：使用几个第i个物品
  • 状态转换：f(i, j) = max { f(i - 1, j), f(i - 1, j - x v_i) + xw_i}

  • 状态转换方程推导如下，最终转换方程为f(i, j) = max{ f(i - 1, j), f(i, j - v_i) + w_i }

    1. /*
    2. f[i][j] = max(f[i - 1][j], f[i - 1][j - v] + w, ...,  f[i -1][j - kv] + kw + ...) 有限项
    3. for j = j -v:
    4. f[i][j - v] = max(f[i - 1][j - v], f[i - 1][j - 2v] + w), ..., f[i -1][j - (k + 1)v] + kw + ...) 有限 - 1项
    5. so:
    6. f[i][j] = max(f[i - 1][j], f[i][j - v] + w)
    7. */

  • 另外多说一句，完全背包问题优化为1维的，但实际上是对二维做了等价变换，相当于在一维数组内存了i的状态和i-1的状态，并巧妙的利用更新顺序，达到了二维的目的。

    数字三角形

  • 集合：f(i,j)，从下往上数第i层，第j个点的所有题解

  • 属性值：路径长度
  • 状态划分：是从(i, j)的左下方上来的，还是从(i, j)的右下方上来的

  • 状态转换：f(i, j) = max(f(i - 1, j)+ v[i][j], f(i - 1, j +1) + v[i][j])

    最长上升子序列

  • 集合：f(i)，前i个数，包含i的所有题解

  • 属性值：最长上升子序列
  • 状态划分：遍历前面所有i-1个状态，加上第i个数之后是否可以+1

  • 状态转换：f(i) = max(比i小的数j的f(j) + 1)

    最长公共子序列

  • 集合：f(i, j)，A字符串前i个字符和B字符串前j个字符的公共子序列的所有题解

  • 属性值：长度最长
  • 状态划分：a[i], b[j]在不在最长公共子序列中
  • 状态转换：f(i, j) = max(f(i - 1, j - 1), f(i - 1, j - 1) + 1, f(i , j - 1), f(i -1, j)) = max(f(i - 1, j - 1) + 1, f(i , j - 1), f(i -1, j))

image.png

最短编辑距离

  • 集合：f(i, j)，A字符串前i个字符和B字符串前j个字符的所有编辑距离
  • 属性值：编辑距离最短
  • 状态划分：假设编辑距离最后一次的操作只涉及a[i]，b[j]（这个假设并不影响最后的结果），则最后一次操作分为在a[i]后面增加、删除a[i]、替换a[i] -> b[j]三种操作

  • 状态转换：f(i, j) = min{ f(i, j - 1) + 1, f(i - 1, j ) + 1， f(i - 1, j -1)需要额外判断a[i]和b[j]是否是相等的}

    石子合并

  • 集合：f(i, j)，从第i个石堆到第j个石堆的所有合并方案

  • 属性值：最小合并代价
  • 状态划分：有(j - i)种合并方案，遍历，选择最优方案

image.png

整数划分

完全背包思考

  • 转化为一个背包容量为n，有n个物品，可以放无数次的完全背包问题，装完之后容量恰巧是n。
  • 集合：f(i, j)，用前i个物品装，体积恰巧为j的题解
  • 属性值：数量
  • 状态划分： ```c // k表示背包最多只能放的下k个i f(i, j) = f(i - 1, j) + f(i - 1, j - i) + f(i - 1, j - 2i) + .. + f(i - 1, j - ki); f(i, j - i) = + f(i - 1, j - i) + f(i - 1, j - 2i) + .. + f(i - 1, j - ki);

f(i, j) = f(i - 1, j) + f(i, j - i);

  1. <a name="VoRFo"></a>
  2. #### 另一种思考
  4. - 集合：f(i, j)表示和为i，总共j个数的集合
  5. - 属性值：数量
  6. - 状态划分
  7. ```c
  8. // 分成两类集合，一类是j个数中的最小值为1，另一类是j个数中的最小值不为1
  9. f(i, j) = f(i - 1, j - 1) + f(i - j, j)

蒙德里安的梦想

image.png

  • 求解思路：只考虑横着的方块，横着的方块摆完，剩下的空间摆竖着的方块，这里有一个限制就是，剩余空间一定要放得下竖着的方块。
  • 集合：f[i, j] 表示前i - 1列已经摆好，第i列方块状态j(二进制表示)的所有集合
  • 属性值：方案数
  • 状态划分：可以发现，由于方块的长度是2，所以，第i列的方案组合，只和第i-1列的方案组合有关。并且由于第i列方块状态是确定的j，i-1列的方块状态k和j是有限制关系的。
  • k和j的限制为，确定了k，j 之后，i - 1的方块状态是k | j，因此，k | j的空隙必须能够放得下竖着的方块。此外，k和j针对同一行，不可能均为1，即 (k & j) == 0。

  • 因此，f[i, j] = sum(f[i - 1, k]), j k满足上述约束。

    最短Hamilton路径


  • 正则匹配

  • 集合：f[i, j]表示s串的前i个字符和匹配模式p串的前j个字符的匹配方案

  • 属性值：是否能匹配
  • 状态划分：s[i]和p[j]的多种情况组合
  • 转移方程：
    1. 如果p[j] != ‘*’, 那么f[i, j] = f[i - 1, j - 1] && s[i]和p[j]是否匹配
    1. 如果p[j] == ‘‘，那么需要遍历能够匹配多少字符串的多种情况，由于*可以匹配0个或者任意个字符，因此有如下转移方程：f[i, j] = f[i, j - 2] (0个) || f[i - 1, j - 2] && s[i]和p[j - 1]能匹配 || f[i - k, j - 2] && s[i-k],…, s[i]均能和p[j - 1]匹配 (k个)，此处，k是有个最大值的，不是无限项。
  • 把i = i - 1代入上述方程：f[i - 1, j] = f[i - 1, j - 2] || f[i - 2, j - 2] && s[i - 1]和p[j - 1]能匹配 || f[i - k - 1, j - 2] && s[i-k-1],…, s[i]均能和p[j - 1]匹配 (k个)

  • 因此f[i, j] = f[i, j - 2] || f[i - 1, j] && s[i]和p[j - 1]能匹配。

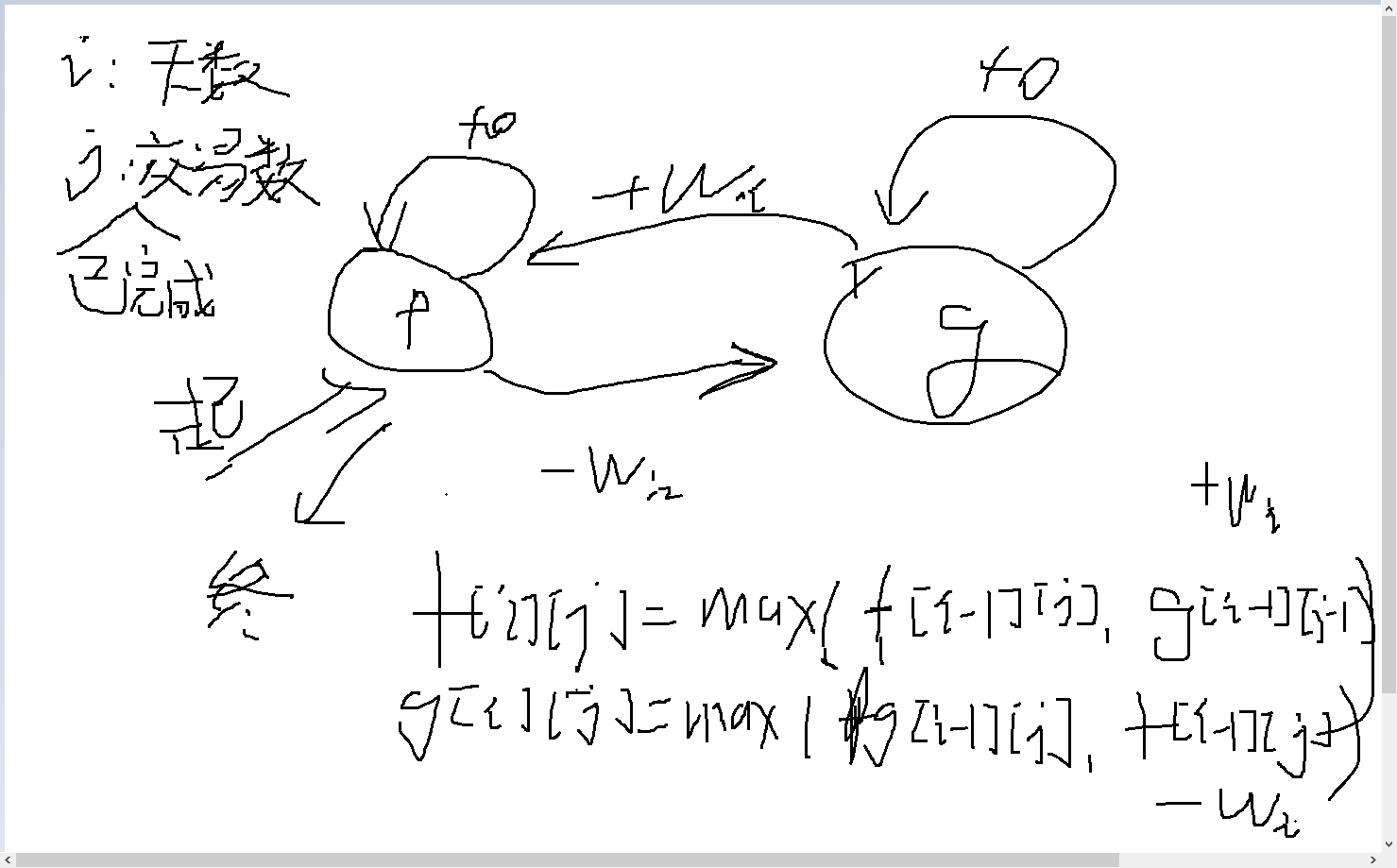
    状态机DP，LeetCode188

  • 状态机DP的做法和一般DP不一样，需要画出状态机的转换方式。每一种状态是一个变量，比如188题里有两个状态，分别表示：手上没有股票的状态，和手上有股票的状态，因此需要f, g才能做出来。

  • 由于有两个状态，转换方程是f, g两个变量得到的。

image.png