LeetCode 834. Sum of Distances in Tree

834. Sum of Distances in Tree

解题思路

该题目需要求解树中每个点到所有点的距离之和，可以通过树形DP来进行求解。
下面是一棵树，最上面的节点时根节点。为了通用性，我们来计算红色节点对应到所有节点的距离。
树形DP其实都是DFS进行计算的，因此我们会从根节点进行DFS。到了红色节点之后，其实要计算的距离分为两部分：第一部分是到子节点的距离，第二部分是从父节点到其余节点的距离。
对于到子节点的距离down[i]，我们可以在DFS中，利用从子节点搜集到的信息直接计算。假设红色节点是i，子节点是j。则down[i] = down[j] + cnt[j]。down[i]表示所有以i为根节点的子节点到i节点的距离。cnt[i]表示以i为根节点，节点数目。
对于从父节点到其余节点的距离up[i]，假设父节点为u，该距离等于父亲到其余节点的距离+节点个数。根据图示，up[i] = up[u]（父节点朝上的距离） +down[u]（父节点朝下的距离） - (down[j] + cnt[j])（父节到j的距离） + (总结点数 - cnt[j])（父节点涉及到的节点数目）。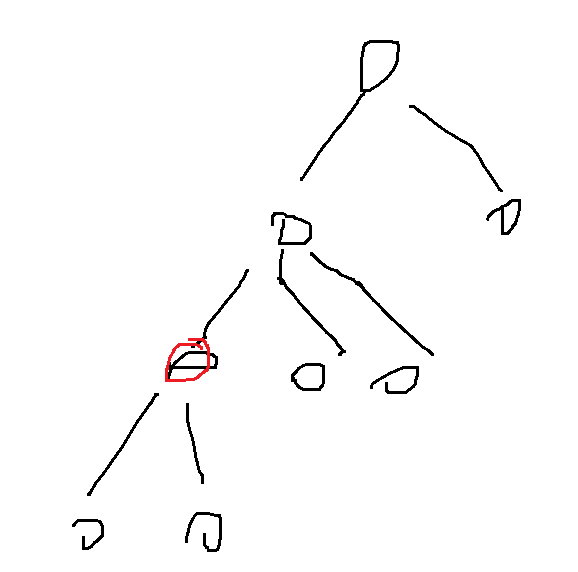

代码

const int N = 20010;
int h[N], e[N], ne[N];
int idx;
int down[N], up[N], cnt[N];
int n;
void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++;
}
class Solution {
public:
    void dfs_down(int u, int father) {
        down[u] = 0;
        cnt[u] = 1;
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j == father) {
                continue;
            }
            dfs_down(j, u);
            down[u] += down[j] + cnt[j];
            cnt[u] += cnt[j];
        }
    }
    void dfs_up(int u, int father) {
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j == father) {
                continue;
            }
            up[j] = up[u] + down[u] - down[j] - cnt[j] + n - cnt[j];
            dfs_up(j, u);
        }
    }
    vector<int> sumOfDistancesInTree(int N, vector<vector<int>>& edges) {
        n = N;
        memset(h, -1, sizeof h);
        idx = 0;
        for (auto e: edges) {
            int a = e[0], b = e[1];
            add(a, b);
            add(b, a);
        }
        dfs_down(0, -1);
        dfs_up(0, -1);
        vector<int> ans;
        for (int i = 0; i < N; i ++) {
            ans.push_back(down[i] + up[i]);
        }
        return ans;
    }
};