《悖论-破解科学史上最复杂的9大谜团》第一章 颠覆你的思考逻辑
- 消息的一块钱之谜
- 贝特箱子悖论 & 小猫问题
- 蒙提霍尔悖论
- 生日悖论
贝特朗箱子悖论
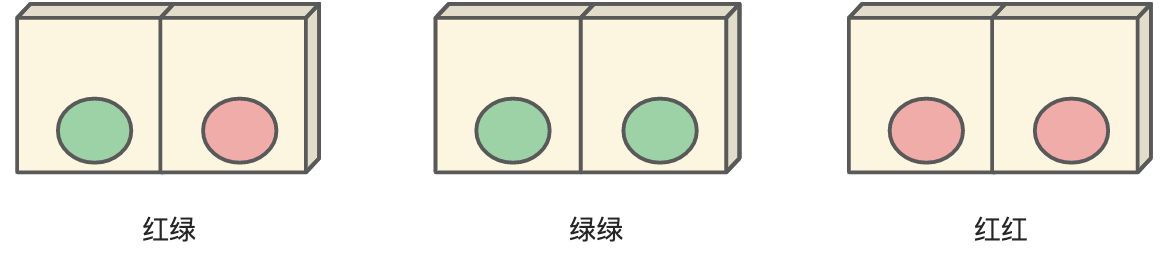
- 有三个箱子,每个箱子里各有两枚硬币
- 每个箱子分成两半,每一半都有一个球,可以单独打开看球的颜色
- 球的颜色有绿色和红色两种
- 箱子里球的搭配分为3种
问题
现在随机选择一个箱子,然后随机打开一半,假设发现的是红球。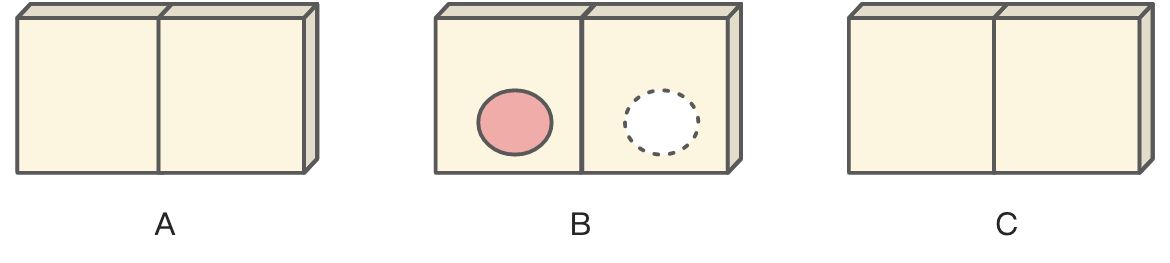
问:另一边也红球的概率是多少?
解答
我相信第一反应都是1/2,因为有红球的情况只有两种, 红红和红绿,所以红红的概率不就是1/2了吗?
但是答案是2/3。
为什么?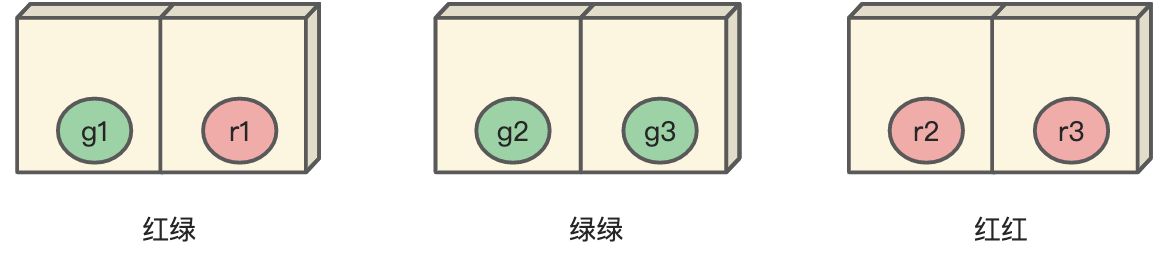
| 首次拿 | 另一半 |
|---|---|
| G1 | R1 |
| G2 | G3 |
| G3 | G2 |
| R1 | G1 |
| R2 | R3 |
| R3 | R2 |
小猫问题
假设你想购买两只猫,打电话给宠物店老板,老板说有两只猫
- 一只花猫,一只橘猫
然后问老板他们的性别,这时候可能有两种回答:
- “检查了其中一只,是公猫”
- “检查了花猫,是公猫”
问:这两种情况下,两只猫都是公猫的概率分别是多少?
解答
- 情况一:1/3
- 情况二:1/2 | 花猫 | 橘猫 | | —- | —- | | 公 | 公 | | 公 | 母 | | 母 | 公 | | 母 | 母 |
蒙提霍尔悖论
假如你现在参加一个节目,主持有让你选择一个箱子,假如选中有红球的箱子可以获得10W元。
已知:
- 有三个箱子
- 一个箱子有球,两个箱子没有球
问题
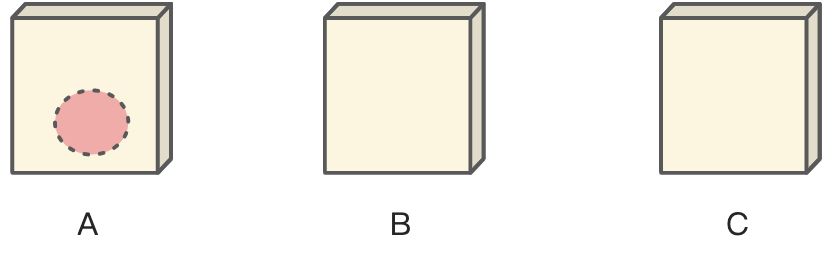
- 假设你随机选择一个箱子,放到A的位置
- 这时主持人打开一个箱子,为空,放到C位置
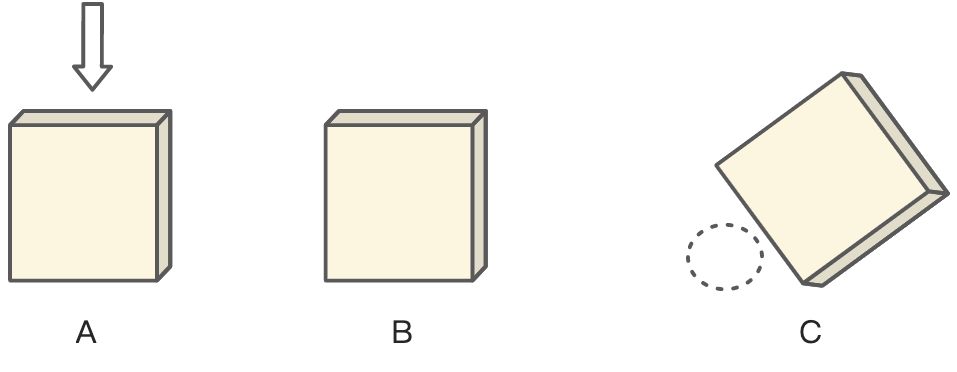
主持人问:你是否愿意交换A和B?
解答
- 如果不交换,猜中的概率为 = 1/3
- 如果交换,猜中的概率为 = 2/3
文字解释:如何交换,问题就从选择有球的箱子变成了选择没有球的箱子。
生日问题
生日问题是指最少需要几人,当中的两个人生日相同的概率才会大于50%。
- 一年365天
- 不存在双胞胎等类似情况
解答
假设有两个人
- 先求不相同的概率
- 得出相同的概率
可以推算出
现在要求 p(n) >= 0.5 时候的n最小值,最终可以求出p(23) = 0.507
扩展一下
现在100个数字,连续随机拿75次,存在重复数字的概率为多少?
这就是HashMap中负载因子为什么为0.75的原因

