博客
MATLAB入门之旅
课程提供
Cody 游戏

一、关键字

关键字

  • ans
  • i，j ：complex number
  • Inf:∞
  • eps:2.2204e-016
  • NaN:not a number
  • pi:Π

  • 为了列举出来所有的关键字可以

    1.        >>iskeyword<br />没有空格；

  • randi 均匀分布的伪随机整数

  • Format

format
自行将输出格式重置为默认值，即浮点表示法的短固定十进制小数点格式和适用于所有输出行的宽松行距。
数值格式仅影响数字显示在命令行窗口输出中的方式，而不是 MATLAB计算或保存它们的方式。
>>format long x
显示多位小数
long（十位）、short（四位小数）、shortE、longE、bank、hex、rat

  • ；分号

不显示运算结果

  • ↑ 方向键

显示之前的指令

  • abs（计算绝对值）
  • eig（计算特征值）

    中英对照

    | 英 | 中 | | —- | —- | | structured programming | 结构化编程 | | loop | 循环 | | subroutine | 子程序 | | | |


二、操作

clear 和clc

clear 函数清理工作区。clc 命令清理命令行窗口
可以使用 clear 函数从工作区中删除所有变量。clear x 可以清除某个变量

“ ; “ 分号

计算但是不显示

执行命令先后顺序

y 的值保持不变，因为 MATLAB 不会在命令行窗口中重新运行以前的命令。
如果您要在修改 m 后重新计算 y，需要重复命令 y = m/2。
现在就试一下！使用向上箭头重新调用命令 y = m/2，然后按 Enter 键。切记，要查看 y 的新值，请不要在命令末尾使用分号。

save保存命令

您可以使用 save 命令将工作区中的变量保存到称为 MAT 文件的 MATLAB 特定格式文件中。
要将工作区保存到名为 foo.mat 的 MAT 文件中，请使用命令：
>> save foo

load加载变量

可以使用 load 命令从 MAT 文件加载变量。
>> load foo
如果只想加载或保存部分变量，可以使用函数的两个输入。从文件 myData.mat 中仅加载变量 m：
>> load myData m
将变量 m 保存到名为 justm.mat 的新 MAT 文件中：
>> save justm m

控制函数精度

虚数 i是 MATLAB 中的内置常量。
在命令行窗口中仅显示前四个小数位。您可以使用 format 函数控制显示的精度。
请试着输入 format long 并显示 x 的值。
输入 format short 可切换回默认显示。

三、快捷方式

  • Ctrl+I 智能缩进

    四、数组

    什么是数组？

    所有 MATLAB 变量均为数组。这意味着每个变量都可以包含多个元素。可以使用数组将相关数据存储在一个变量中。

image.png

创建数组

可以使用方括号创建包含多个元素的数组。
>>x = [3 5]
当您用空格（或逗号）分隔数值时，MATLAB 会将这些数值组合为一个行向量，行向量是一个包含一行多列的数组 (1×n)。
当用分号分隔数值时，MATLAB 会创建一个列向量 (n×1)

创建等间距向量

我们经常需要创建一些包含等间距数值的向量，例如以下向量。
>>y = [5 6 7 8]
对于长向量，输入单个数值是不实际的。
可用来创建等间距向量的替代便捷方法是使用 :

  • 知道间隔

运算符并仅指定起始值和最终值。
>>y = 5:8
y = 5 6 7 8
注意：当使用冒号运算符时，不需要方括号
:运算符使用默认的间距 1，但是可以指定您自己的间距，如下所示。
>>x = 20:2:26
x = 20 22 24 26

  • 知道元素个数

如果知道向量中所需的元素数目（而不是每个元素之间的间距），则可以改用 linspace 函数：
linspace(first,last,number_of_elements)
注意，请使用逗号 (,) 分隔 linspace 函数的输入。
>>x = linspace(0,1,5)
x = 0 0.250 0.500 0.750 1.000

  • 矩阵转置

linspace 和 : 运算符都可创建行向量。
可以使用转置运算符 (‘) 将行向量转换为列向量。
>>x=1:3;
>>x=x’ (矩阵转置，结果以列输出)
在创建时，也可以转置矩阵
可以通过在一条命令中创建行向量，并将其全部转置来创建列向量。注意此处使用圆括号来指定运算的顺序
x=(1:2:5)’ （1 3 5以列输出）

创建数组函数

MATLAB 包含许多函数，可帮助您创建常用的矩阵，
随机数矩阵。
>>x = rand(2)
x = 0.8147 0.1270
0.9058 0.9134
请注意，rand(2) 命令中的 2 指定输出将为一个 2×2 的随机数矩阵。
许多矩阵创建函数允许输入一个数值来创建方阵 (n×n)，或者输入两个数值来创建非方阵。
rand(2) 22矩阵
rand(2,3) 23矩阵
使用 size 函数知道现有矩阵大小。
size(x)
也可以使用一行代码创建与现有矩阵大小相同的矩阵。
rand(size(x))

数组索引

  • 使用行、列索引从数组中提取值。

y = A(5,7)
此语法将会提取 A 的第 5 行第 7 列的值，然后将结果赋给变量 y。
可以使用 关键字 end 作为行或列索引来引用最后一个元素。
>>y = A(end,2) 最后一行第二列
可以将算术运算与关键字 end 结合使用。例如：
y = A(end-1,end-2)
如果只对一个矩阵使用一种索引，它将按顺序从上到下遍历每列。
创建一个变量 y，并用 y 作为 data 的索引。
>>y=4
>>n=data(y） n等于data数组的第四个元素

  • 用冒号：
  • 指代该维度中的所有元素。

x = A(2,:) 第二行的所有列（第二行所有元素）

  • 引用某个值范围。

x = A(1:3,:) 创建一个包含矩阵 A 的第 1 行、第 2 行和第 3 行所有元素的矩阵。

  • 单个索引值范围可用于引用向量元素的子集。（没有逗号）

x = v(3:end)
返回向量 v 的一个子集，其中包含从第三个到最后一个元素范围内的所有元素。

  • 非连续索引

索引可以是非连续数字
>>m=[1 3 6]
>>p=density(m)
density 的第一个、第三个和第六个元素。

逻辑索引

  • 关系运算符（例如 >、<、== 和 ~=）执行两个值之间的比较。相等或不相等比较的结果为 1 (true) 或 0 (false)。
  • 您可以使用关系运算符将某个向量或矩阵与单个标量值进行比较。结果是与原始数组相同大小的逻辑数组。
    >>[5 10 15] > 12

ans = 0 0 1

  • 可以使用逻辑数组作为数组索引，在这种情况下，MATLAB 会提取索引为 true 的数组元素。以下示例将会提取 v1 中大于 6 的所有元素。
    >>v = v1(v1 > 6)

v = 6.6678 9.0698

  • 也可以对两个不同向量使用逻辑索引。
    >>v = sample(v1 > 6)

s = 18 23
使用 < 运算符创建一个逻辑数组，然后使用该数组对变量进行索引。
c = a(b < 4)

  • 可以使用逻辑索引在数组中重新赋值。例如，如果要将数组 x 中等于 999 的所有值都替换为值 1。
    >>x(x==999) = 1
  • 您可以使用逻辑运算符 and (&) 以及 or (|) 来组合逻辑比较。
    要查找小于 4 且大于 2 的值，请使用 &：

x = v1(v1<4 & v1>2)
要查找大于 6 或小于 2 的值，请使用 |：
x = v1(v1>6 | v1<2)

对向量执行数组运算

  • 可以将一个标量值与数组中的所有元素相加。
    >>y = x + 2
  • 可以将任意两个大小相同的数组相加。
    >>z = x + y
  • 可以将数组中的所有元素与某个标量相乘或相除

z=2*x
>>y=x/3

  • MATLAB 中的基本统计函数可应用于某个向量以生成单个输出。可以使用 max 函数来确定向量的最大值。
    >>xMax = max(x)

    c =
    5 6 9
    9 56 4
    22 33 55
    >> e=max(c)
    e =
    22 56 55

  • MATLAB 的函数可在单个命令中对整个向量或值数组执行数学运算。

xSqrt = sqrt(x)

  • 运算符执行矩阵乘法。因此，如果使用 将两个大小相同的向量相乘，则由于内部维度不一致，您将会收到一条错误消息。
    >>z = [3 4] * [10 20]

错误使用 * <br />用于矩阵乘法的维度不正确。
而 . 运算符执行按元素乘法，允许您将两个大小相同的数组的对应元素相乘。
>>z = [3 4] . [10 20]
z = 30 80

获取多个函数的输出

  • size 函数可以应用于数组，以生成包含数组大小的单个输出变量。

s = size(x)

  • size 函数可以应用于矩阵，以生成单个输出变量或两个输出变量。使用方括号 ([ ]) 获得多个输出。
    >>[xrow,xcol] = size(x)
  • 可以使用 max 函数确定向量的最大值及其对应的索引值。max 函数的第一个输出为输入向量的最大值。执行带两个输出的调用时，第二个输出为索引值。
    >>[xMax,idx] = max(x)
  • 如果只需函数的第二个输出，可以使用波浪号字符 (~) 忽略特定输出。
    例如，可能只需要包含向量中最大值的索引：

density = data(:,2)
[~,ivMax] = max(v2)
densityMax = density(ivMax)

五、绘制数据图

绘制向量图

  • 可以使用 plot 函数在一张图上绘制两个相同长度的向量。

plot(x,y)
使用 loglog 函数（用法同 plot 函数），在每个坐标轴上使用对数刻度绘制数据。
>>loglog(x,y,”*—“)

  • plot 函数接受一个附加参数。使用该参数，您可以通过在引号中包含不同符号的方式来指定与之对应的颜色、线型和标记样式。
    plot(x,y,”r—o”)

以上命令将会绘制一条红色 (r) 虚线 (—)，并使用圆圈 (o) 作为标记。可以在线条设定的文档中了解有关可用符号的详细信息。

  • 每个绘图命令都创建了一个单独的绘图。要在一张图上先后绘制两条线，要使用 hold on 命令保留之前的绘图，然后添加另一条线。
  • 启用保留状态时，将继续在同一坐标区上绘图。要恢复默认绘图行为，即其中每个绘图都有自己的坐标区，要输入 hold off。
  • 单独绘制一个向量时，MATLAB 会使用向量值作为 y 轴数据，并将 x 轴数据的范围设置为从 1 到 n（向量中的元素数目）。
  • plot 函数接受可选的附加输入，这些输入由一个属性名称和一个关联的值组成。
    plot(y,”LineWidth”,5)

以上命令将绘制一条粗线。可以在线条属性文档中了解更多可用属性的详细信息。

  • 使用 plot 函数时，可在绘图参数和线条设定符之后添加属性名称-属性值对组。
    >>plot(x,y,”ro-“,”LineWidth”,5)
  • plot 函数用来绘制线条。MATLAB 中还有许多其他绘图函数。可以在 MATLAB 图库中看到一个详尽的列表。
    每个绘图都有其不同的自定义选项。

  • 可以使用 xlim 函数放大所关注的区域。
    xlim([xmin xmax])

    编写绘图注释

  • 可以使用绘图注释函数（例如 title）在绘图中添加标签。此类函数的输入是一个字符串。MATLAB 中的字符串是用双引号 (“) 引起来的。
    >>title(“Plot Title”)

  • 可以使用 ylabel 函数对y轴添加标签
  • 可以使用 legend 函数为绘图添加图例。
    legend(“a”,”b”,”c”) 第一条为“a ”线

可以将字符串数组直接传递给 legend 函数。
>>legend(a) a为数组

  • 您可以在绘图注释中使用变量的值，方法是将字符串与变量串联起来：
    >>bar(data(3,:))
    >>title(“Sample “ + sample(3) + “ Data”)

    六、导入数据

    以表的形式导入数据

  • 要提取表变量，可以使用圆点表示法：
    data.VariableName data 是表的名字，后边是列或者行的名字

  • 如果正在使用表，一般可能希望将相关数据放在一起。您可以将计算结果赋给表，而不是创建单独的变量。

data.HeightMeters = data.HeightYards*0.9144
如果变量 data.HeightMeters 不存在，MATLAB 将在表中创建名为 HeightMeters 的新变量。

七、编程

函数

  • if else end

仅当条件为 true 时，才执行 if 代码块的主体。
elseif 关键字可在 if 后使用，以添加更多条件。您可以包括多个 elseif 代码块。

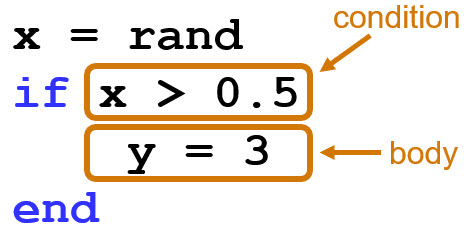
image.png

  • for end

运行以下代码时，循环体将被执行三次，因为循环计数器 (c) 通过 1:3（1、2 和 3）进行计数
如果要对未知长度的向量执行循环，可以改用 length 函数：
for idx = 1:length(x)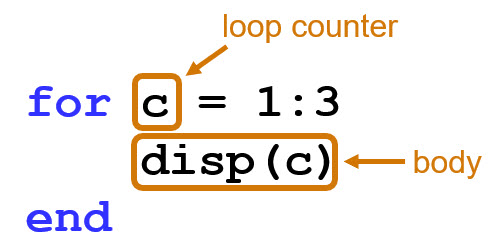
image.png

八、MATLAB 入门之旅摘要

基本语法

示例 说明
x=pi 使用等号 (=) 创建变量。
左侧 (x) 是变量的名称，其值为右侧 (pi) 的值。
y=sin(-5) 可以使用括号提供函数的输入。

桌面管理

函数 示例 说明
save save data.mat 将当前工作区保存到 MAT 文件中。
load load data.mat 将 MAT 文件中的变量加载到工作区。
clear clear 清除工作区中的所有变量。
clc clc 清除命令行窗口中的所有文本。
format format long 更改数值输出的显示方式。

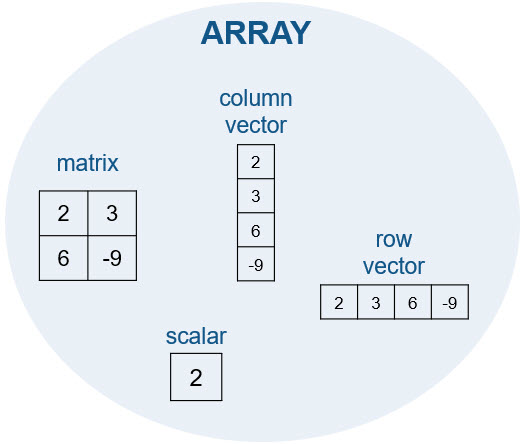
数组类型

示例 说明
4 标量
[3 5] 行向量
[1;3] 列向量
[3 4 5;6 7 8] 矩阵

等间距向量

示例 说明
1:4 使用冒号 (:)
运算符，创建一个从 1 到 4，间距为 1 的向量。
1:0.5:4 创建一个从 1 到 4，间距为 0.5 的向量。
linspace (1,10,5) 创建一个包含 5 个元素的向量。这些值从 1 到 10 均匀间隔。

创建矩阵

示例 说明
rand (2) 创建一个 2 行 2 列的方阵。
zeros (2,3) 创建一个 2 行 3 列的矩形矩阵。

索引

示例 说明
A(end,2) 访问最后一行的第二列中的元素。
A(2,:) 访问第二行所有元素。
A(1:3,:) 访问前三行的所有列。
A(2) = 11 将数组中第二个元素的值更改为 11。

数组运算

示例 说明
[1 1; 1 1]*[2 2;2 2]
ans =
4 4
4 4		 执行矩阵乘法。
[1 1; 1 1].*[2 2;2 2]
ans =
2 2
2 2		 执行按元素乘法。

多个输出

示例 说明
[xrow,xcol] = size(x) 将 x 中的行数和列数保存为两个不同变量。
[xMax,idx] = max(x) 计算 x 的最大值及其对应的索引值。

文档

示例 说明
doc randi 打开 randi 函数的文档页。

绘图

示例 说明
plot (x,y,”ro-“,”LineWidth”,5) 绘制一条红色 (r) 虚线 (—)
并使用圆圈 (o) 标记，线宽为5。
hold on 在现有绘图中新增一行。
hold off 为下一个绘图线条创建一个新坐标区。
title (“My Title”) 为绘图添加标签。
legend(“a”,”b”)
legend(a) a为数组		 可以使用 legend 函数为绘图添加图例。
可以将字符串数组直接传递给 legend 函数。

使用表

示例 说明
data.HeightYards 从表 data 中提取变量 HeightYards。

| | data.HeightMeters = data.HeightYards*0.9144 | 从现有数据中派生一个表变量。 |

逻辑运算

示例 说明
[5 10 15]>12 将向量与值 12 进行比较。
v1(v1>6) 提取 v1 中大于 6 的所有元素。
x(x==999) = 1 用值 1 替换 x 中等于 999 的所有值。

编程

示例 说明
if x > 0.5
y = 3
else
y = 4
end		 如果 x 大于 0.5，则将 y 的值设置为 3。

否则，将 y 的值设置为 4。 | | for c = 1:3
disp(c)
end | 循环计数器 (c) 遍历
值 1:3（1、2 和 3）。
循环体显示 c 的每个值。 |

九、视窗解读

编辑器

image.png

fx

image.png
点击，有许多基础的函数
image.png

注释

image.png
可以将某一句注释起来（不执行）
或者右键选择也可以，或者使用快捷键Crtl+R注释和Crtl+T取消注释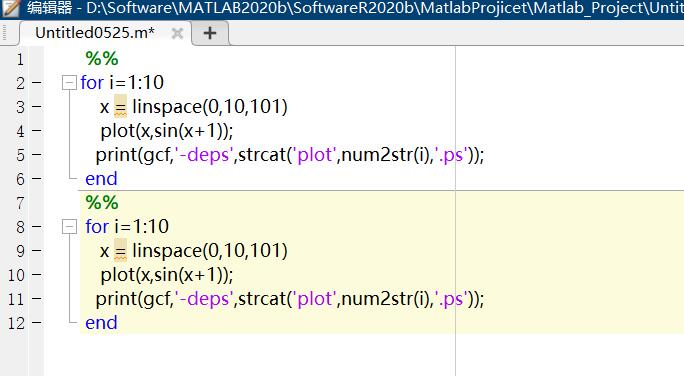
image.png
一个%符号注解一行，两个%%可以把代码分节，这个时候，运行节和运行就不一样了
image.png

调试

在代码区段数字面前点一下，会有个灰色的圆点出现（代码保存后，那个圆点可能会为红色）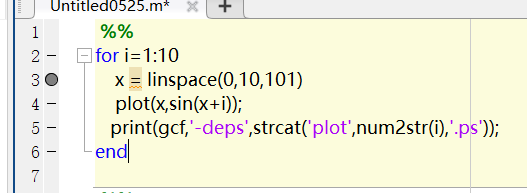
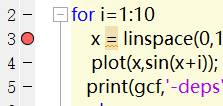
image.pngimage.png
在点击运行后，会执行到断点处，下方命令行窗口也会改变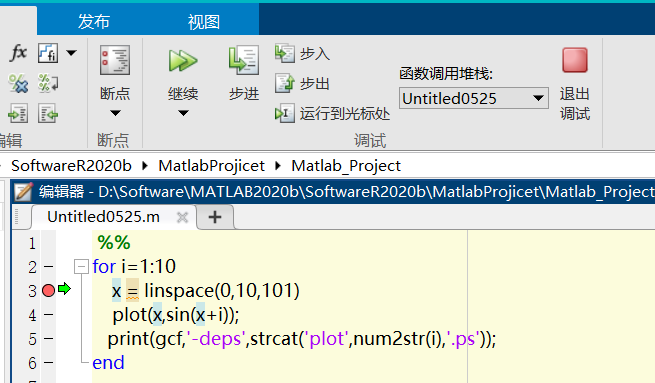
image.png
>>变为K>>
点击红色方块🟥退出调试，就可以恢复原来的样子

>> '文件名'
K>>

image.png

十、解方程

基本了解solve

clear
clc
1
sym(1)
x=sym('x')
syms a b c
%创建符号变量
y=a+b
z=sqrt(c)
%根号
f(x) = x+1
f(1)
subs(y,a,1)
%把y中的a替换成1
z1=subs(z,c,2)
vpa(z1)
%求解z的近似值

x+1=0、ex+2=10

syms x
%创建符号变量
eq1=x+1 == 0
solve(eq1)
eq2=exp(x+2) == 10
solve(eq2)

ax^2+bx+c=0

syms x
syms a b c
eq3 = a*x^2+b*x+c == 0
solve(eq3)
%不指定求解的变量，默认为X
solve(eq3,a)

方程的通解

sin(x)=1

 syms x 
eq=sin(x)==1
solve(eq) 
 %输出，只输出了一个解
ans =

pi/2

如果解包含参数，并且设置了ReturnConditions为true<br />solve函数返回带参数的解和该解成立所满足的条件<br />否则，solve函数要么返回有自行选择的参数值给出的具体解<br />要么返回不给定特定值的参数化的解（很少）<br />可以使用结构数组形式获取求解结果

syms x 
eq=sin(x)==1;
%
[solx,p,c]=solve(eq,x,'ReturnConditions',true)
%结构数组
S=solve(eq,x,'ReturnConditions',true)
S.x
S.parameters
S.conditions


%输出
solx = pi/2 + 2*pi*k
p = k
 %工作空间变量中不存在k,要使用k必须用p或者再声明一个syms k
c = in(k, 'integer')
%输出
S = 

  包含以下字段的 struct:

             x: [1×1 sym]
    parameters: [1×1 sym]
    conditions: [1×1 sym]


ans =

pi/2 + 2*pi*k


ans =

k


ans =

in(k, 'integer')

特定区间的值

cos(x)=-1在[0，2pi]的解

思路：计算通解，计算满足区间的参数值k,把参数值回代通解，获得在该区间的解

syms x 
eq=sin(x)==1;
[solx,p,c]=solve(eq,x,'ReturnConditions',true)

%求解k
eq2=[solx>0,solx<2*pi]
assume(c)        %需要是整数，使用conditions 中的c
[solk,pk,ck]=solve(eq2,p,'ReturnConditions',true)
%回代
vx=subs(solx,p,solk)

解方程组

x^2+y^2=5,x+y=3

注意：在有多个输出变量时，（比如上一个让输出[x,y]），尽量不要指定为 输入方程的变量名 ，因为指定后，不能保证就是按照你指定的顺序输出的
默认,solve 按照字母顺序求解变量
如果要指定顺序[y,x]=solve(eq[y,x])可以（待定）

syms x y
eqs=[x^2+y^2==5,x+y==3] 
%%如果没有[solx,soly]
solve(eqs)
%输出为
ans = 

  包含以下字段的 struct:

    x: [2×1 sym]
    y: [2×1 sym]


 %%输出
 [solx,soly]=solve(eqs)
solx =

2
1


soly =

1
2

%%利用上式计算(x-y)*exp(x^2+y)的值
S=solve(eqs)
subs((x-y)*exp(x^2+y),S)

x+1=0,x+2=0

syms x
eq=[x+1==0,x+2==0]
solve(eq,x)

%输出

ans =

Empty sym: 0-by-1

实数解或常用解

实数解solve-Real
常用解solve-PrincipalValue

x^3=1在复数域和实数域的解

syms x
eq=x^3+1==0
solve(eq,x)
% 三个数据
ans =

                  -1
1/2 - (3^(1/2)*1i)/2
(3^(1/2)*1i)/2 + 1/2
solve(eq,x,'Real',true)            %ans =-1

sin(x)+cos(x)=1的通解和常用解

syms x
eq=sin(x)+cos(x)==1;
solve(eq,x)
solve(eq,x,'ReturnConditions',true)
solve(eq,x,'PrincipalValue',true)

%  1
ans =

pi/2
   0

%  2
ans = 

  包含以下字段的 struct:

             x: [2×1 sym]
    parameters: [1×1 sym]
    conditions: [2×1 sym]

%  3,常用解，只返回一个结果 
ans =

0

使用简化或忽略假设

简化solve-IgnoreAnalyticConstraints
忽略假设solve-IgnoreProperties
设置IgnoreAnalyticConstraints属性为true 时，使用简化规则
包括：log(a)+log(b)=log(a*b)
log(a^b)=blog(a)
log(exp(x))=x
asin(sinx)=x
注意：简化不一定正确，例如log((-1)^2)!=2log(-1)
MTLAB是按照符号进行运算的

exp(log(x)*log(x))=2

syms x
eq = exp(log(x)*log(x))==2
solve(eq,x)
solve(eq,x,'IgnoreAnalyticConstraints',true)

%输出
%%  1

警告: Unable to solve symbolically. Returning a numeric solution using vpasolve. 
> 位置：sym/solve (第 304 行) 

ans =

- 22.618785642798602662469454045255 - 2.9003114448643861325799628957195i

 %%   2
ans =

 exp(log(2)^(1/2))
exp(-log(2)^(1/2))

x^2+x-2=0在x>0条件下和忽略该假设的解

syms x positive
eq = x^2+x-2==0
solve(eq,x)
solve(eq,x,'IgnoreProperties',true)        %忽略x为正数的条件
syms x clear



ans =

1


ans =

-2
 1

警告: SYMS X CLEAR and SYMS('X','CLEAR') will not accept CLEAR in a future release.
SYMS X clears assumptions by default. 
> 位置：syms (第 191 行)

高阶多项式方程

高阶多项式方程显示解solve-MaxDegree
注意：求解高阶时，很难用显式解析式表达，因此符号解中可能会包含root字符
MaxDegree只接受小于五的整数，因为，一般情况下，高于四阶的多项式没有显式表达式的解

x^3+x^2+1=0

syms x
eq=x^3+x^2+1==0
solve(eq,x)
%%输出

ans =

root(z^3 + z^2 + 1, z, 1)
root(z^3 + z^2 + 1, z, 2)
root(z^3 + z^2 + 1, z, 3)

solve(eq,x,'MaxDegree',3)

%%输出
ans =

                                                                                                              - 1/(9*(29/54 - (31^(1/2)*108^(1/2))/108)^(1/3)) - (29/54 - (31^(1/2)*108^(1/2))/108)^(1/3) - 1/3
1/(18*(29/54 - (31^(1/2)*108^(1/2))/108)^(1/3)) - (3^(1/2)*(1/(9*(29/54 - (31^(1/2)*108^(1/2))/108)^(1/3)) - (29/54 - (31^(1/2)*108^(1/2))/108)^(1/3))*1i)/2 + (29/54 - (31^(1/2)*108^(1/2))/108)^(1/3)/2 - 1/3
(3^(1/2)*(1/(9*(29/54 - (31^(1/2)*108^(1/2))/108)^(1/3)) - (29/54 - (31^(1/2)*108^(1/2))/108)^(1/3))*1i)/2 + 1/(18*(29/54 - (31^(1/2)*108^(1/2))/108)^(1/3)) + (29/54 - (31^(1/2)*108^(1/2))/108)^(1/3)/2 - 1/3

s=solve(eq,x,'MaxDegree',3);
pretty(s)
vpa(s)


 %%输出
 /                  1         1              \
|              - ---- - #1 - -              |
|                9 #1        3              |
|                                           |
|                 /   1       \             |
|         sqrt(3) | ---- - #1 | 1i          |
|   1             \ 9 #1      /      #1   1 |
| ----- - ------------------------ + -- - - |
| 18 #1               2               2   3 |
|                                           |
|         /   1       \                     |
| sqrt(3) | ---- - #1 | 1i                  |
|         \ 9 #1      /        1     #1   1 |
| ------------------------ + ----- + -- - - |
\             2              18 #1    2   3 /

where

         / 29   sqrt(31) sqrt(108) \1/3
   #1 == | -- - ------------------ |
         \ 54           108        /



ans =

                                      -1.4655712318767680266567312252199
0.23278561593838401332836561260997 - 0.79255199251544784832589830065336i
0.23278561593838401332836561260997 + 0.79255199251544784832589830065336i

使用roots求解

roots([1 1 0 1])

ans =

  -1.4656 + 0.0000i
   0.2328 + 0.7926i
   0.2328 - 0.7926i

数值求解法

数值解法vpasolve
方程的左边 lhs
方程的右边 rhs
如果solve 不能找到解（解析解）
并且设置了ReturnConditions为true，返回空解并给出警告
否则，solve函数在内部会调用函数vapsolve 尝试寻找数值解
对于非多项式方程或者方程组，数值解法只返回找到的第一个解（如果解存在）

sin(x)=exp(x)靠近坐标原点最近的点

syms x
eq = sin(x)  ==exp(x)
solve(eq,x)
vpasolve(eq,x)

%%输出

警告: Unable to solve symbolically. Returning a numeric solution using vpasolve. 
> 位置：sym/solve (第 304 行) 
%不能求出符号解，使用vpa返回了一个数值解
ans =

-226.19467105846511316931032359612


ans =

-226.19467105846511316931032359612

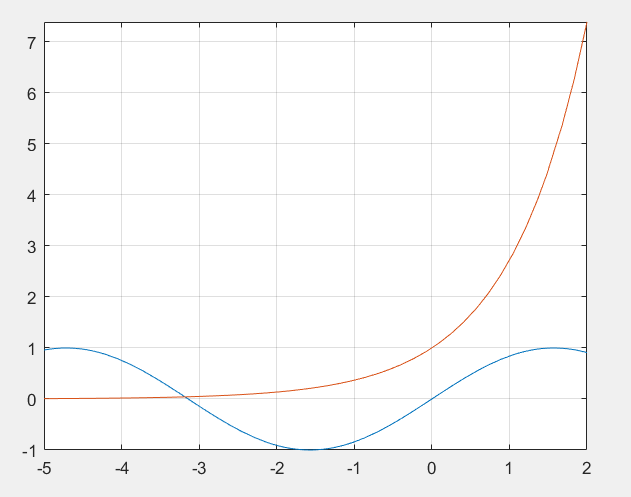
syms x
eq = sin(x)  ==exp(x)
fplot([lhs(eq),rhs(eq)],[-5,2])        %设置区间
grid on        %网格打开


%使用vpa函数，规定求解区间
vpasolve(eq,x,[-4,-3])  
%%输出
ans =

-3.1830630119333635919391869956364

image.png

求解不等式

说明：求解不等式，其实就是求解满足不等式的全部解

一元一次不等式

syms x
eq = 2*x+1<0;
solve(eq,x)
solve(eq,x,'ReturnConditions',true)

%%输出
ans =
                              %找到一个解就停止
-3/2


ans = 

  包含以下字段的 struct:

             x: [1×1 sym]
    parameters: [1×1 sym]
    conditions: [1×1 sym]

%%添加参数
[solx p c]=solve(eq,x,'ReturnConditions',true)

%%输出

solx =

x


p =

x


c =

x < -1/2

一元二次不等式（含参）

a<0时，求解3x^2-4a*x+a^2<0

syms x a
eq = 3*x^2-4*a*x+a^2<0
assume(a<0)
[solx p c]=solve(eq,x,'ReturnConditions',true)
pretty(c)
simplify(c)

实例

(x+3)^2=(1-2*x)^2

syms x
eq = (x+3)^2==(1-2*x)^2;
solve(eq,x)

%%输出
ans =

-2/3
   4

2*x/(3-x)=1-2/(x-3)

syms x
eq = 2*x/(3-x)==1-2/(x-3)
solve(eq,x)

%%输出
ans =

5/3

方程组 x(y+1)+y(1-x)=2,x*(x+1)-y-x^2=0

syms x y
eq1= x*(y+1)+y*(1-x)==2
eq2= x*(x+1)-y-x^2==0
[solx,soly]=solve([eq1,eq2],[x,y])

%%输出

solx =

1


soly =

1