spfa /tarjan /线段树

STL标准库 语法

include

数据结构

vector——

https://www.yuque.com/yizhixiaoxiongzaifei/ug2d1v/fb6dd38a-cd1f-4658-a15c-ab71970f2a8a

1.push_back 在数组的最后添加一个数据 2.pop_back 去掉数组的最后一个数据 3.at 得到编号位置的数据 4.begin 得到数组头的指针 5.end 得到数组的最后一个单元 + 1 的指针 13.erase 删除(迭代器) 15.rbegin 将 vector 反转后的开始指针返回 (其实就是原来的 end-1) reverse_iterator 16.rend 将 vector 反转构的结束指针返回 (其实就是原来的 begin-1) 17.empty 判断 vector 是否为空 18.swap 与另一个 vector 交换数据

可以使用!= 和==判断两个列表是否包含的元素数量相同且相同位置元素值相同。
可以用for(auto& i:vec){i=…;} 改变vector内的值。

list——

  • queue
  • stack
  • deque
    • O(nlgn)
  • map
  • unordered_map
  • set
  • multiset
    • 注意multiset的删除要用迭代器，否则会同时删除多个

      priority_queue(自定义比较函数)

      1. struct cmp
      2. {
      3. bool operator ()(int a, int b) //重载小于
      4. { return a > b; }
      5. };
      6. priority_queue<int,vector<int>,cmp>;
      默认的比较函数是less，是大根堆
      如果要小根堆 需要greater
      自定义比较函数需要用struct重载()

一般算法

  • 数学计算
    • accumulate
    • power
    • max
    • min
  • 基础数据处理
    • swap
    • iter_swap
    • reverse
    • itoa
    • atoi
  • 查找：
    • find
    • search
    • binary_search
    • lower_bound ——algorithm 大于等于目标值的第一个元素
    • upper_bound ——algorithm 大于目标值的第一个元素

可以用cmp<函数，表示cmp(val,x)成立的第一个元素

  • nth_element
  • max_element
  • min_element
    • 排序
  • sort
    • 字符串string
  • 正则regex
  • substr
  • find

    文件输入输出

    读文件 ```cpp

    include

//1. 头文件

include

using namespace std;

int main() { //2. 创建流 ifstream input;

  1. //3. 打开文件，将流与文件相关联
  2. //2, 3步可以直接合并为：ifstream input("number.txt");
  3. input.open("number.txt");
  5. //4. 从文件读入数据
  6. int number1, number2, number3;
  7. input >> number1 >> number2 >> number3;
  9. cout << "number1: " << number1 << endl;
  10. cout << "number2: " << number1 << endl;
  11. cout << "number3: " << number1 << endl;
  13. //5. 关闭流
  14. input.close();
  16. return 0;

}

  1. 写文件
  2. ```cpp
  3. #include <iostream>
  5. //1. 头文件<fstream>
  6. #include <fstream>
  8. using namespace std;
  10. int main()
  11. {
  12.     //2. 创建流
  13.     ofstream output;
  15.     //3. 打开文件，将流与文件相关联，这里使用相对路径
  16.     output.open("number.txt");
  18.     //4. 向文件写入数据
  19.     output << 1 << " " << 2 << " " << 3 << endl;
  21.     //5. 关闭流
  22.     output.close();
  24.     return 0;
  25. }

专题

图论算法

欧拉路径

半欧拉图<->有欧拉通路<->所有点在一个连通分量上,除了两个点(起点和终点)外入度=出度，起点出度=入度+1，终点入度=出度+1
欧拉图<->有欧拉回路<->所有点在同一个强连通分量,所有点入度=出度

hierholzer 算法

从起点出发，进行深度优先搜索。
每次沿着某条边从某个顶点移动到另外一个顶点的时候，都需要删除这条边。
如果没有可移动的路径，则将所在节点加入到栈中，并返回。
原理：死胡同节点会先被入栈。
332. 重新安排行程

最短路径算法

单源点最短路径dijkstra的优先队列优化(正权)

  1. vector<bool> visited(n);
  2. vector<int> distance(n,MAX);
  3. priority_queue<pair<int,int>,vector<pair<int,int>,cmp>> pq;
  4. pair<int,int> p(0,0);
  5. pq.push_back(p);
  6. while(!pq.empty()){
  7.     pair<int,int>& t=pq.top();
  8.     int x=t.first,d=t.second;
  9.     if(visited[x]){continue;}
  10.     visited[x]=true;
  11.     distance[x]=t.second;
  12.     pq.pop();
  13.     for(map<int,int>::iterator it=edge[t].begin();u!=edges[t].end();it++){
  14.         if(visited[u]) continue;
  15.         int u=it.first;
  16.         pair<int,int> q(u,d+it.second);
  17.         pq.push(q);
  18.     }
  19. }

负权单源点最短路径spfa(可检测负环)

  1. struct Edge
  2. {
  3.     int to,len;
  4. };
  5. bool spfa(const int &beg,//出发点
  6.           const vector<list<Edge> > &adjlist,//邻接表，通过传引用避免拷贝
  7.           vector<int> &dist,//出发点到各点的最短路径长度
  8.           vector<int> &path)//路径上到达该点的前一个点
  9. //没有负权回路返回0
  10. //福利：这个函数没有调用任何全局变量，可以直接复制！
  11. {
  12.     const int INF=0x7FFFFFFF,NODE=adjlist.size();//用邻接表的大小传递顶点个数，减少参数传递
  13.     dist.assign(NODE,INF);//初始化距离为无穷大
  14.     path.assign(NODE,-1);//初始化路径为未知
  15.     list<int> que(1,beg);//处理队列
  16.     vector<int> cnt(NODE,0);//记录各点入队次数，用于判断负权回路
  17.     vector<bool> flag(NODE,0);//标志数组，判断是否在队列中
  18.     dist[beg]=0;//出发点到自身路径长度为0
  19.     cnt[beg]=flag[beg]=1;//入队并开始计数
  20.     while(!que.empty())
  21.     {
  22.         const int now=que.front();
  23.         que.pop_front();
  24.         flag[now]=0;//将当前处理的点出队
  25.         for(list<Edge>::const_iterator//用常量迭代器遍历邻接表
  26.                 i=adjlist[now].begin(); i!=adjlist[now].end(); ++i)
  27.             if(dist[i->to]>dist[now]+i->len)//不满足三角不等式
  28.             {
  29.                 dist[i->to]=dist[now]+i->len;//更新
  30.                 path[i->to]=now;//记录路径
  31.                 if(!flag[i->to])//若未在处理队列中
  32.                 {
  33.                     if(NODE==++cnt[i->to])return 1;//计数后出现负权回路
  34.                     if(!que.empty()&&dist[i->to]<dist[que.front()])//队列非空且优于队首（SLF）
  35.                         que.push_front(i->to);//放在队首
  36.                     else que.push_back(i->to);//否则放在队尾
  37.                     flag[i->to]=1;//入队
  38.                 }
  39.             }
  40.     }
  41.     return 0;
  42. }

多源点最短路径

Floyed算法 O(n3)

cost[i][j]=min(cost[i][j],cost[i][k]+cost[k][j]);

  1. cost初始化为初始路径，cost[i][i]=0,其他为最大。
  2. for(int k=0;k<n;k++){
  3.     for(int i=0;i<n;i++){
  4.         for(int j=0;j<n;j++){
  5.             if(i!=j&&cost[i][k]!=MAX&&cost[k][j]!=MAX)
  6.                 cost[i][j]=min(cost[i][j],cost[i][k]+cost[k][j]);
  7.         }
  8.     }
  9. }

最小生成树

最小生成树能够保证整个拓扑图的所有路径之和最小,但不能保证任意两点之间是最短路径。

prim+优先队列

和dijkstra长得一模一样，就是入栈的pair为(节点编号,这条路的长度)

Kruskal+并查集

很熟，略了。
就是注意并查集不要漏find

强连通分量

个人程考复习简要笔记 - 图1

拓扑排序

用队列，每次都弹出度为0的点就好了

  1. // 有向无环图一定存在拓扑序
  2. void TopSort()
  3. {
  4.     // 维护入度为0的节点，编号从小到大排序，保证编号小的节点的拓扑序小
  5.     priority_queue<int, vector<int>, greater<int> > que;
  6.     // 将入度为0的节点加入队列
  7.     for(int i=1; i<=NumVertex; ++i)
  8.     {
  9.         if(Graph[i][0] == 0) que.push(i);
  10.     }
  11.     // 循环处理入度为0的节点，并赋予拓扑序
  12.     int cnt = 0;
  13.     while(!que.empty())
  14.     {
  15.         int u = que.top();
  16.         que.pop();
  17.         // 将最较小拓扑序号赋给入度为0且当前编号最小的节点
  18.         TopNum[u] = ++cnt;
  19.         // 删除节点u出发的边，并调整其它节点的入度
  20.         for(int i=1; i<Graph[u].size(); ++i)
  21.         {
  22.             // 将调整后入度为0的节点加入队列
  23.             if(--Graph[Graph[u][i]][0] == 0) que.push(Graph[u][i]);
  24.         }
  25.     }
  26.     // 图中存在环则无拓扑序
  27.     if(cnt != NumVertex) return;
  28.     // 如果图并不一定是全联通的，那么判原图的某一连通域中是否存在环：
  29.     for(int i=1; i<=NumVertex; ++i) if(Graph[i][0]) puts("somerwhere of the graph has a cycle");
  31.     // 输出以拓扑序排列的节点编号
  32.     for(int i=1; i<=NumVertex; ++i) NodeNum[TopNum[i]] = i;
  33.     for(int i=1; i<=NumVertex; ++i) printf("%d%c", NodeNum[i], i==NumVertex?'\n':' ');
  34. }

花式DFS、BFS

并查集

set&&union代码略
685. 冗余连接 II

二分查找

分治

partition
merge
快排

贪心

最早截止期优先

记得这个只能在给出的条件是[开始时间，截止时间]的时候用，其他条件都需要改。
630. 课程表 III
这个题是有一些变化的EDF，给的是[持续时间，最晚截止时间]，最早截止期优先+优先队列对持续时间排序贪心替换。

动态规划

  • 最大子矩阵
  • 最长上升子序列O(nlgn)算法

滑动窗口/双指针

位运算

  • a^(~a) 去掉最后的1
  • 状压dp枚举所有子集 for(int s=a;s!=0;s=(s-1)&a)

  • 找到最后的1：a&-a

    树

  • 二叉树

  • haffman树
  • 字典树
  • 线段树/树状数组

    搜索

    递归与回溯

  • 装错信封的错排问题

    1. f(n)=(n-1)*(f(n-1)+f(n-2))

  • 极大极小算法

  • dfs
  • bfs

高精度

  • 加
  • 减
  • 乘

  • 除

    字符串

  • 正则表达式

    数学

  • 最大公约数,最小公倍数 ```cpp int gcd(int a,int b){ return b?(b,a%b):a;
    }

int lcm(int a,int b){ return a*b/gcd(a,b); } ```

  • 摩尔投票求众数
  • 两个堆求数据流中的中位数
  • 快速幂√

    线性代数

    Cross Product 向量叉乘

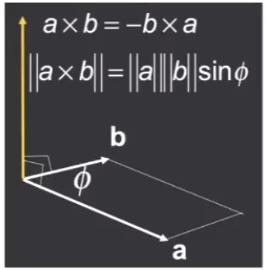
    个人程考复习简要笔记 - 图2
    方向由右手螺旋定则确定，大小为形成的平行四边形面积。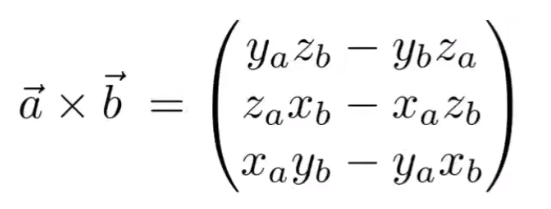
    个人程考复习简要笔记 - 图3
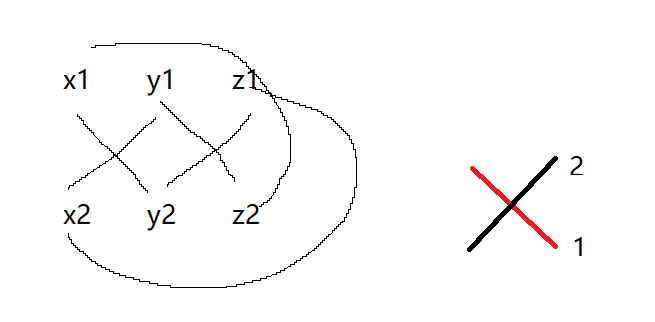
    image.png
    可以简单记为除去自己所在axis的其他axis对角线相乘的差。
    a×b=-b×a

    向量点乘dot

    image.png

个人常见bug汇总

笔误

张冠李戴，把一个变量写成另一个

image.png
第一次写的时候把arr.size()写成了n，tmp[0]也写成了n
这里需要返回的是在新的列表中的顺序，计算时候也应该使用新的列表的数量。

符号写反

min,max相关错误

image.png
min初始值应该为MAX,max初始值应该为MIN
注意min max不要写反。

&&||写反

if(s[i]>’9’||s[i]<’0’){return false;}//不是数字不是点
写成了&&

边界情况没有仔细考虑

image.png
这里的目标是将一个n维向量降为ceil(n/2)大小的向量，这里只考虑到单数情况下需要将中间值直接插入的情况，但忘记了普遍的偶数情形中最后一个位置仍需要普通的处理流程。

等价情况考虑不全

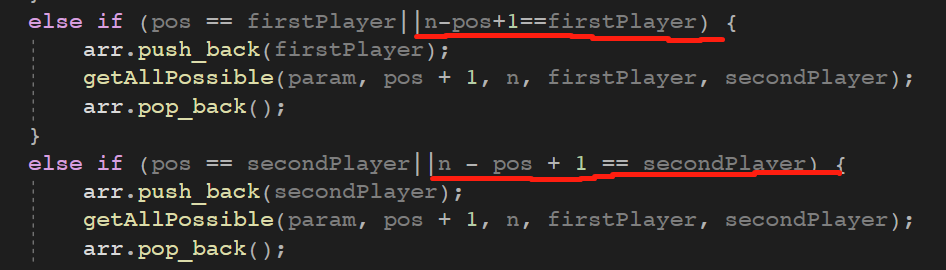
image.png

写漏了

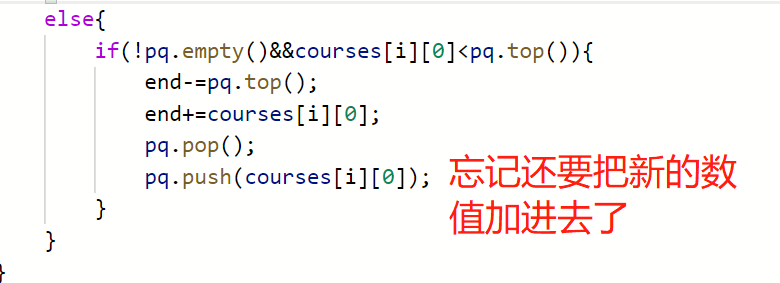image.png替换的时候只记得删不记得增

剪不断理还乱想不明白非常爆炸

二分法
image.png
mid只会==left是不可能等于right的
所以当nums[mid]==nums[r]的时候，只可能是左边有和右边nums[r]一样大的，直接把右边去了比较好。
[2,1,1]

为什么left会出错?
nums[mid]>nums[left]同样证明在左边,nums[mid]nums[mid]==nums[left]可能在左边可能在右边
如果把右边r左移了，可能会出现最小的数直接失踪的情况，如果把左边l移动了，也可能 左边的l就是mid，也丢了orz
感觉是很难写明白的。