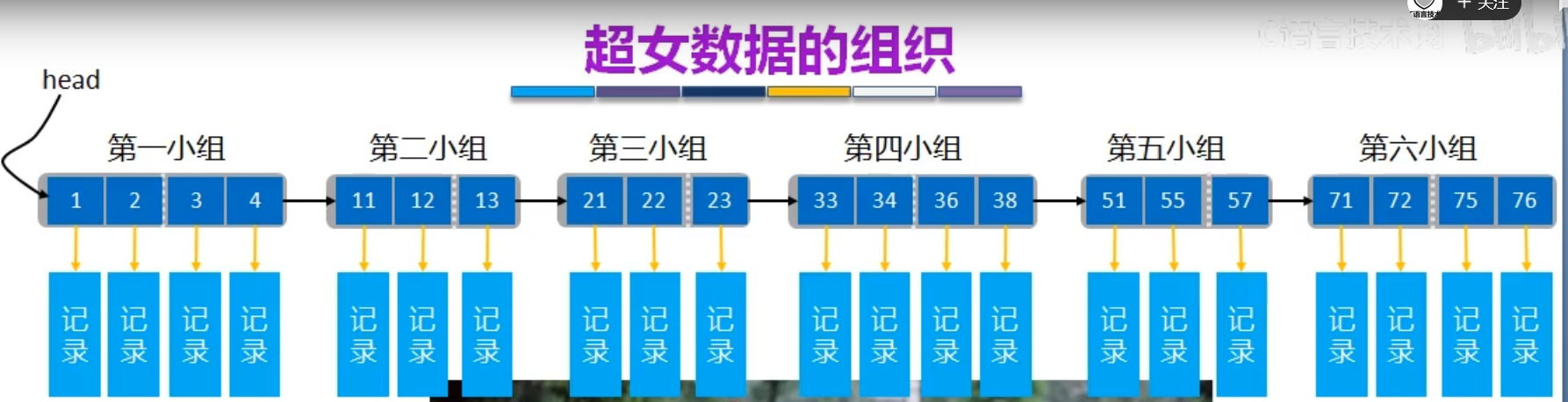
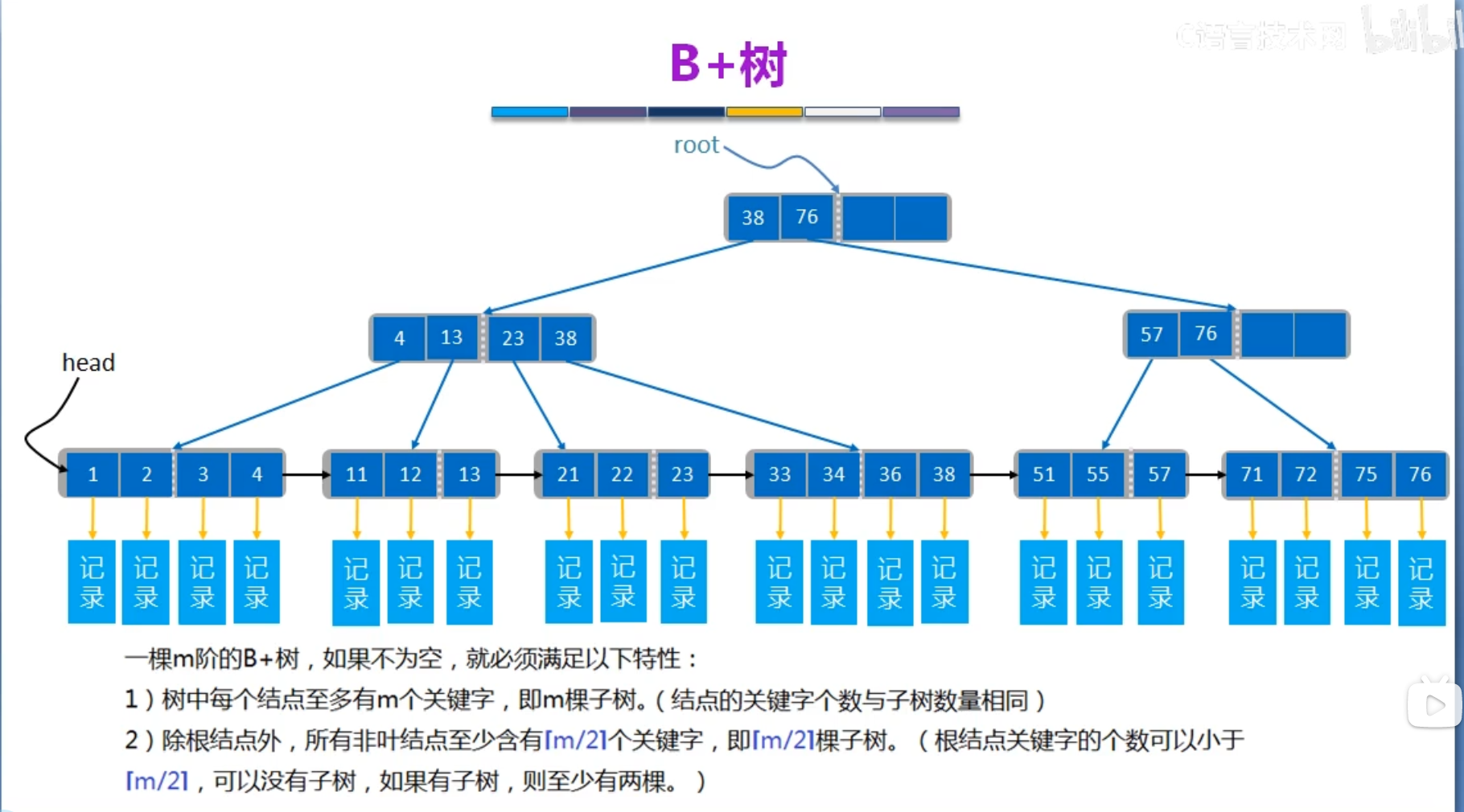
1.磁盘I/O问题
我们知道计算机访问磁盘所带来的开销是十分巨大的。对于一段需要访问磁盘的程序,程序的运行时间几乎都花费到了磁盘I/O上面。也就是说,如果我们可以将磁盘的访问次数减少一般,那么程序的运行时间也将减少一半。
当数据量小时,我们完全可以存储到内存中,数据的访问速度就很快,类似AVL树,红黑树等数据结构,可以将操作数据的时间复杂度降低到O(log2N)。当数据量很大时,无法将其存储在内存当中,只能退而求其次,存储在磁盘中;由于磁盘I/O速度的限制,此时大O模型将不再适用,磁盘的I/O次数决定了程序的时间成本。
针对数据被存储在磁盘中的情况,常规的平衡二叉树已经不能很好的满足我们的需求。因此,我们需要一种新的查找树结构,这种新的树结构可以在相同数据量时拥有更低的高度(树的高度决定了数据操作的最大访问次数)。
B树
B树又叫做平衡多叉树,就是让树具有更多的分支,所以就能降低树的高度,故能增加查找的速度,B树的每一个节点都能存储信息,这就是B树和B+树的区别,由于它是查找树,所以需要有一个排序的依据,将此排序的依据成为关键码,每一个关键码对应着具体的数据元素,所有有多少关键码就有多少的数据。
问:B树的排序依据是什么,同一层的节点从左到右依次递增,每一个节点的左子树都小于这个节点,每一个节点的右子树都大于这个节点。
B树的特点,对于M阶的B树来说
- 根节点或是一片叶子,获具有2-M个孩子节点
- 非叶子节点,具有K-1个关键码,具有K个孩子,其中ceil(M/2)<=K<=M
- 每一个叶子节点都包含k-1个关键码,其中ceil(M/2)<=K<=M.
-
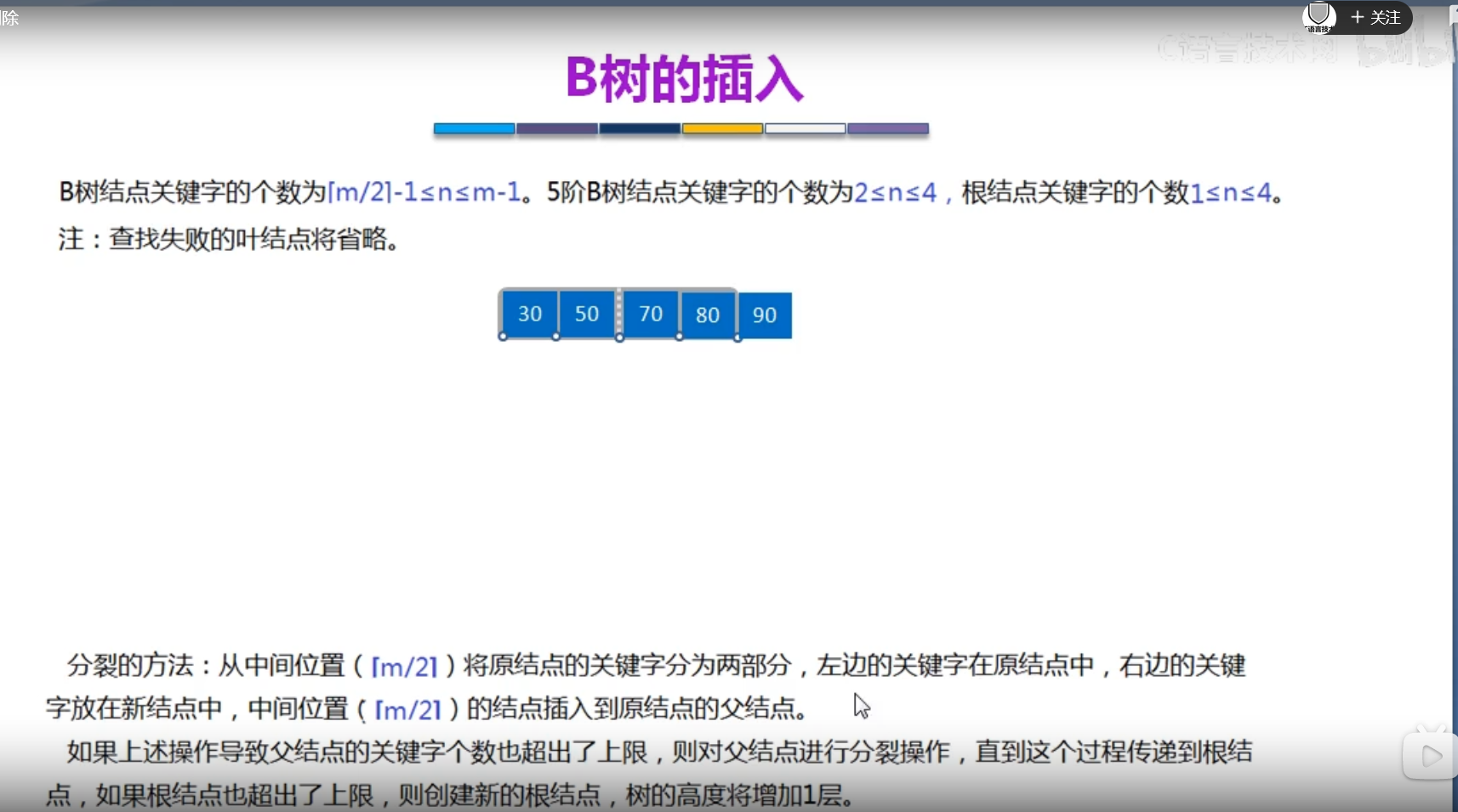
B树的插入操作
插入的原则
如果插入后的关键码小于等于M-1,则直接插入
- 如果插入后的关键码大于M-1.则进行分裂递归
- 分裂操作相当于父节点插入了一个新元素,递归向上进行插入操作
以M = 5为例(即一颗5阶的B-树),图例中绿色代表新插入的元素,蓝色代表插入前就已经存在的元素:
1.像空树插入4

2.紧接着插入1,9,10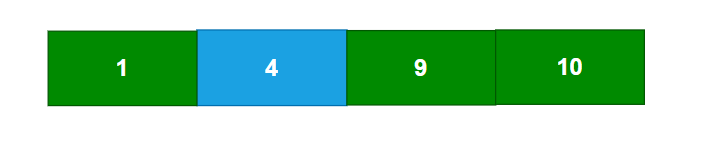
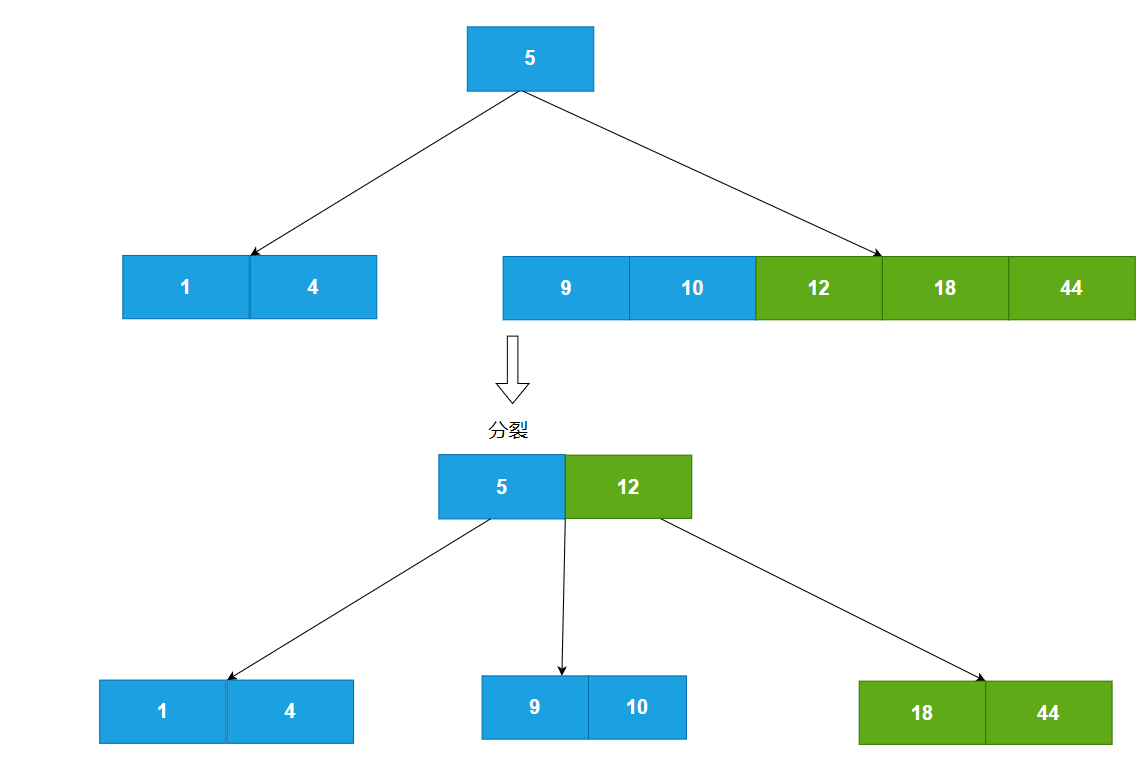
3.紧接着插入5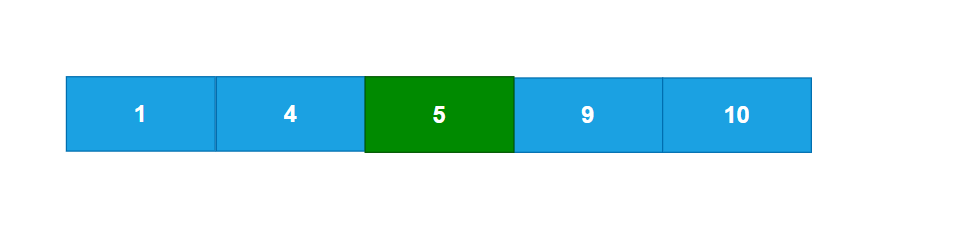
此时它的关键码大于M-1,所以要进行分裂操作,分裂后如图所示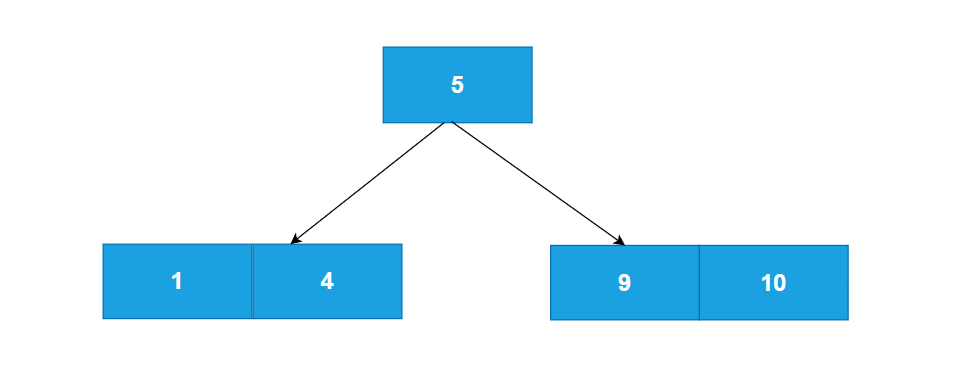
4.接着插入18,12,44
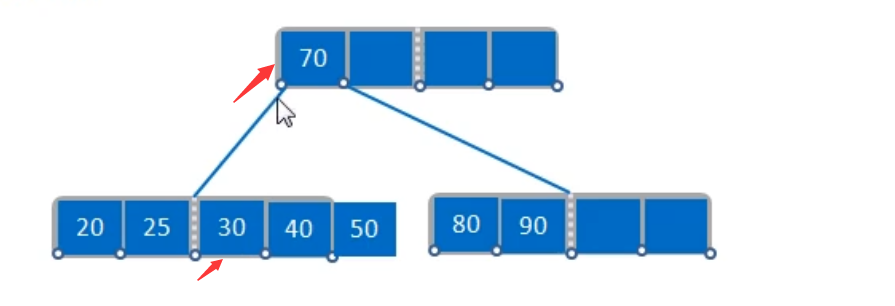
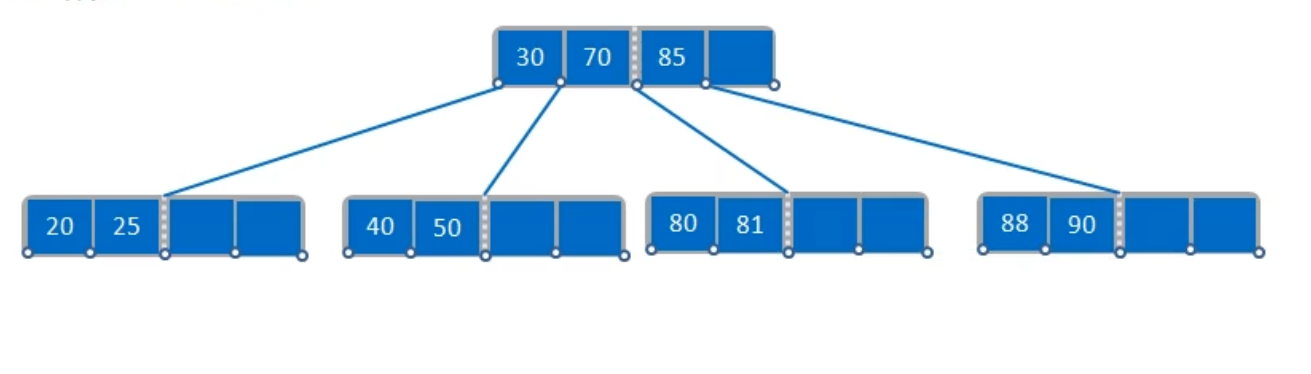
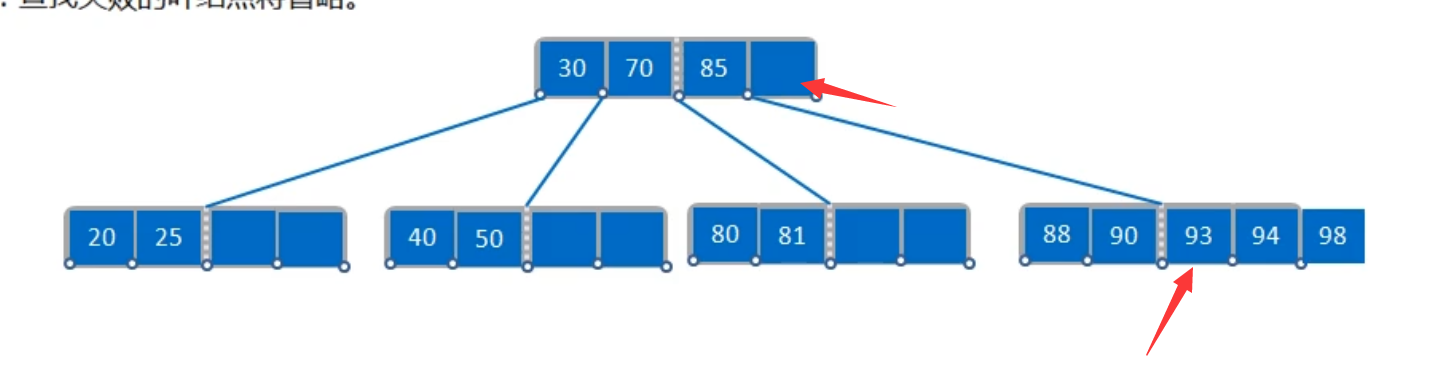
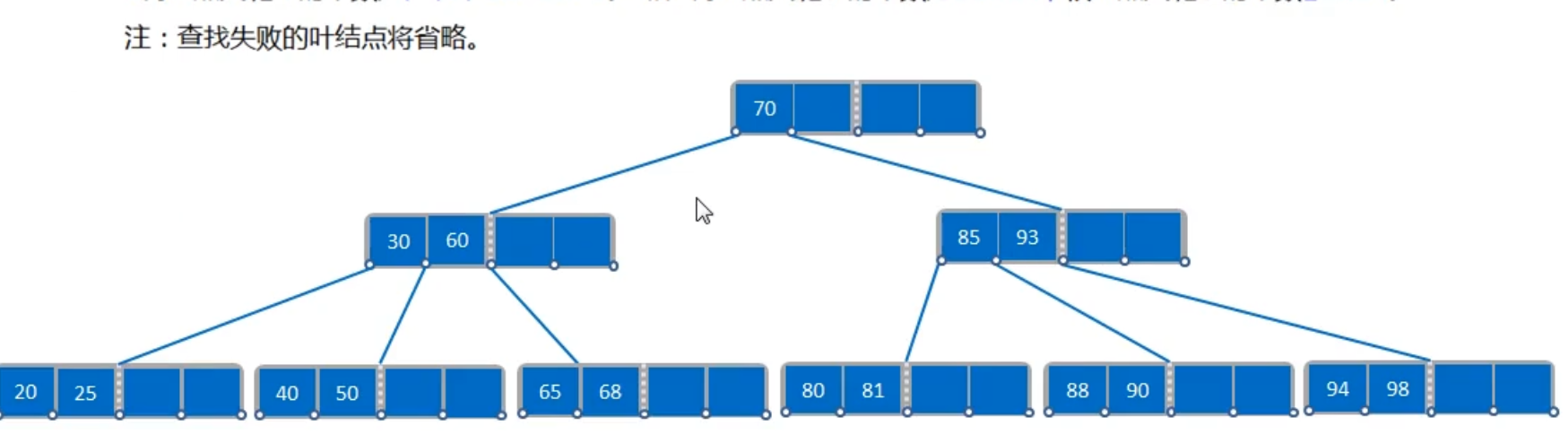
B树的删除操作
删除的原则
- 被删除的节点位于最后一侧的节点,且删除后不破坏B-树规则,则直接删除
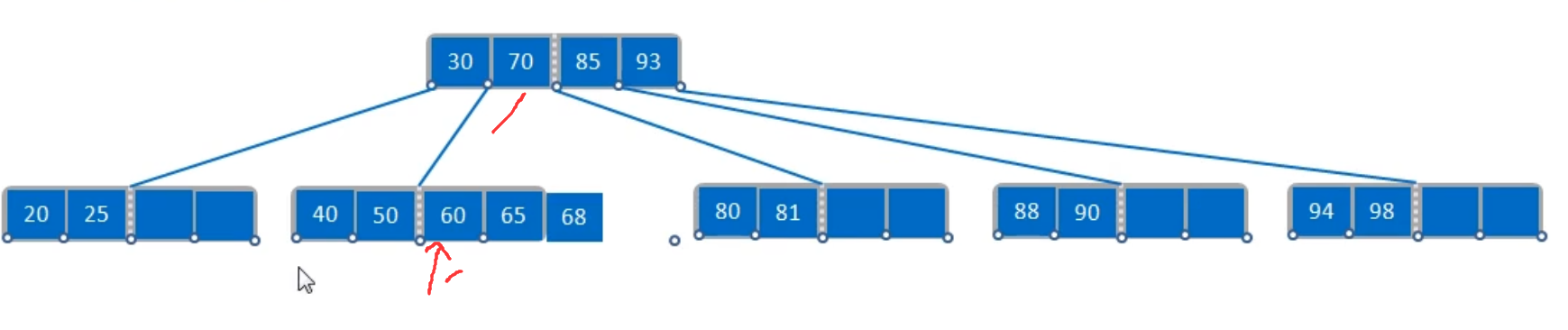
- 被删除的关键码位于叶子节点,删除后该节点关键码个数小于ceil(M/2)-1,则根据其兄弟节点的关键码个数,执行借关键码(兄弟节点的关键码足够)或合并(兄弟节点的关键码不足)操作;
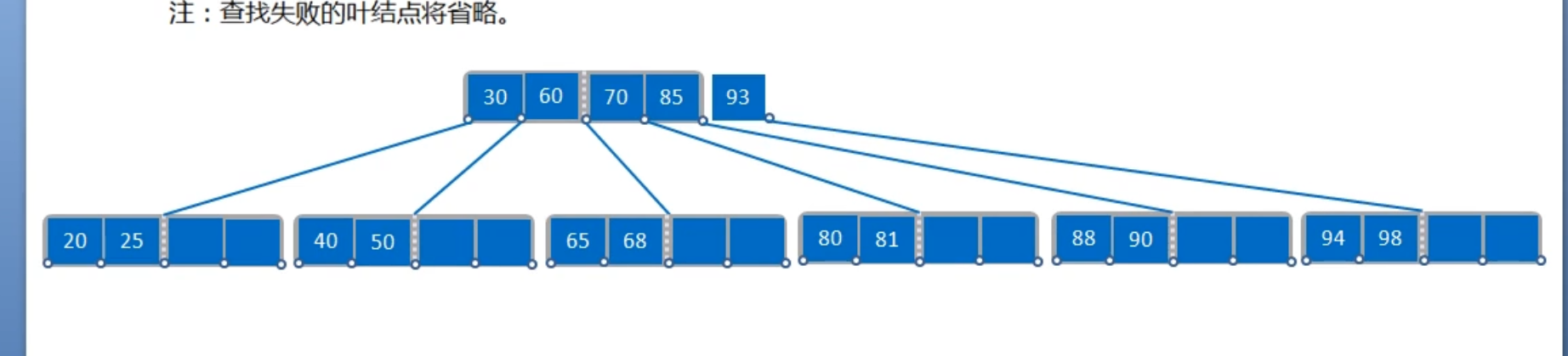
- 合并叶子节点后,父节点的关键码-1,相当于删除了内部节点的关键码,递归的执行删除逻辑即可;
- 被删除的关键码位于内部节点,则根据该关键码的左右子节点的关键码个数,执行借关键码(子节点的关键码足够)或合并(子节点的关键码不足)操作;类似的,合并后递归的向上执行删除逻辑。
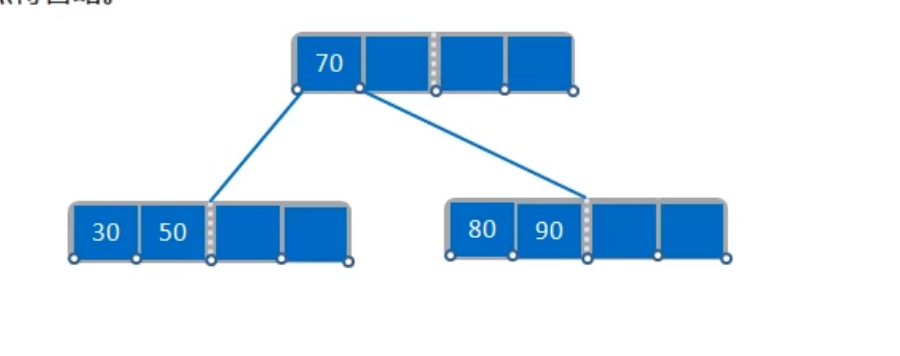
首先看看二叉排序树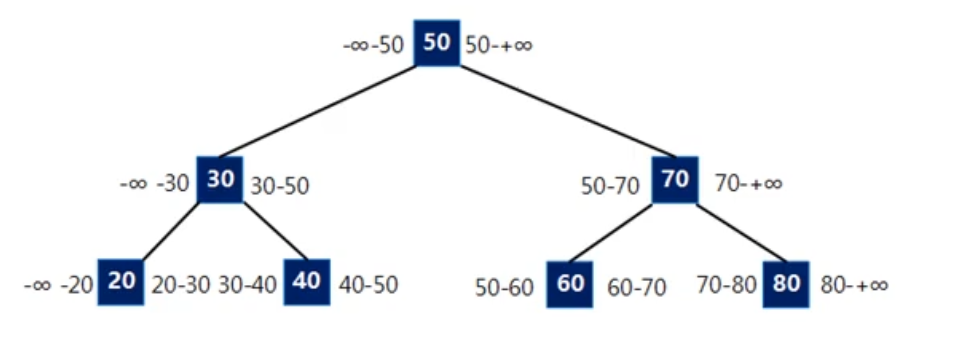
二叉排序树只有一个关键字,一个关键字只有把查找区间一分而二
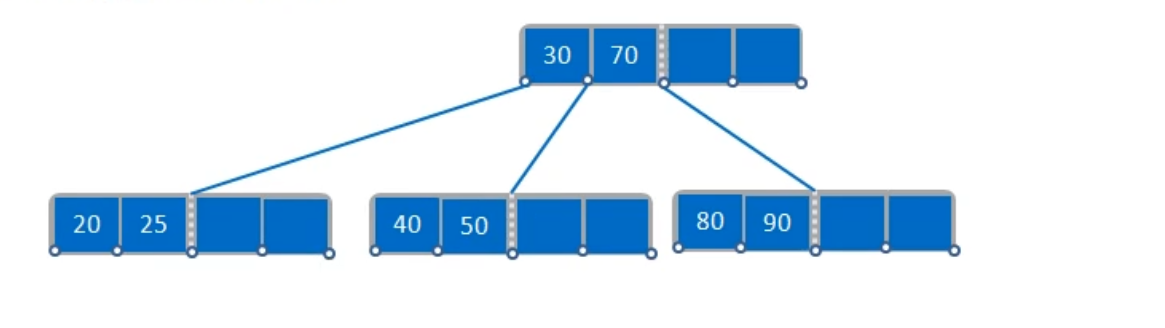
看看多叉排序树
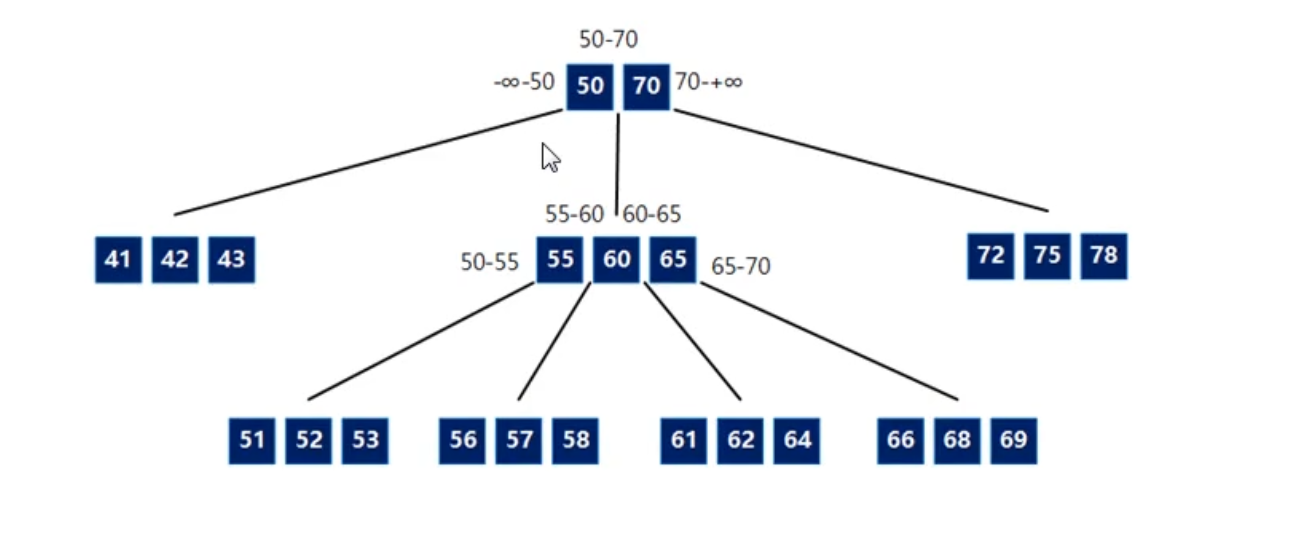
每个节点有多个关键字,多个关键字,就可以把查找区间分为多个

空指针位查找失败的情况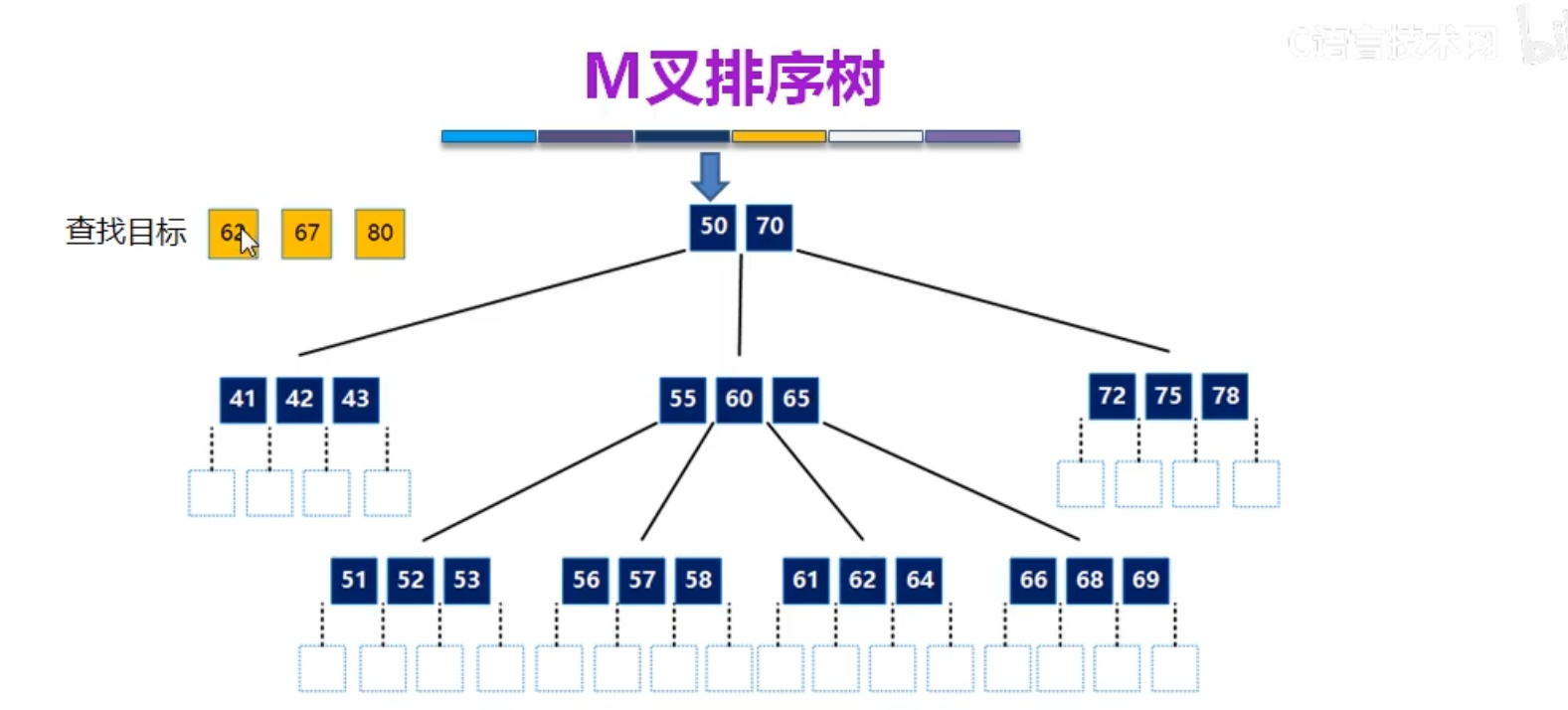
基本概念和性质
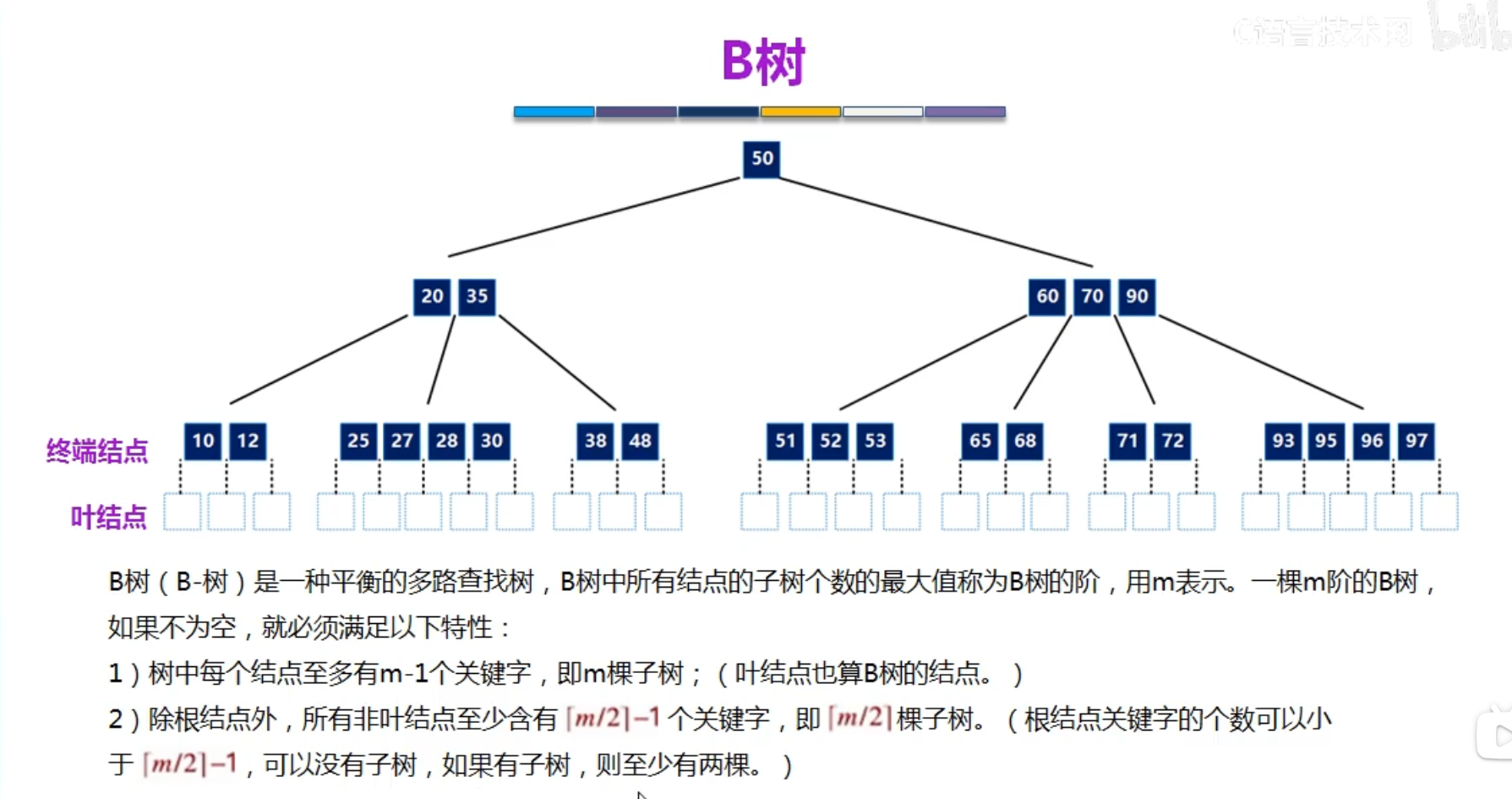
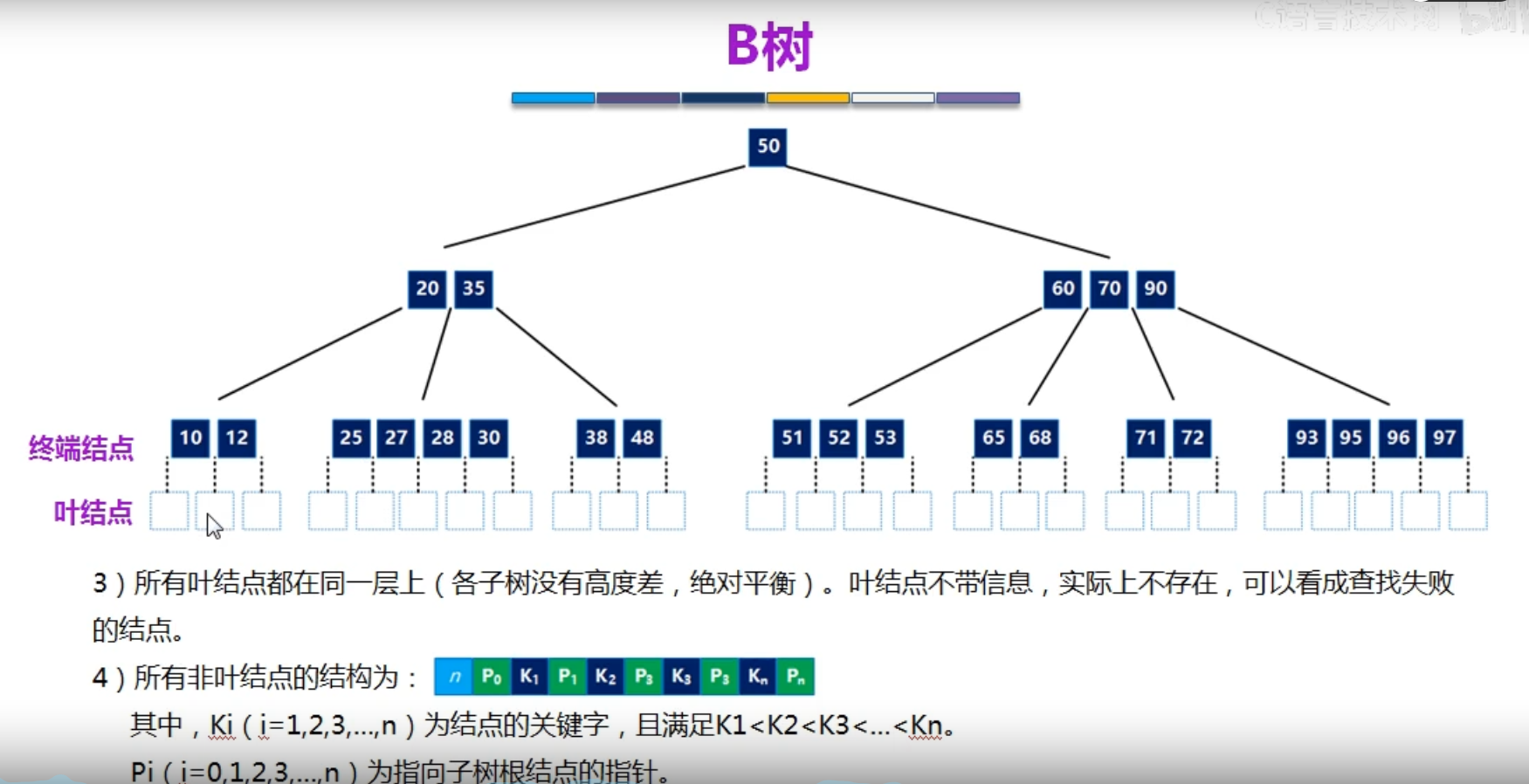
基本操作
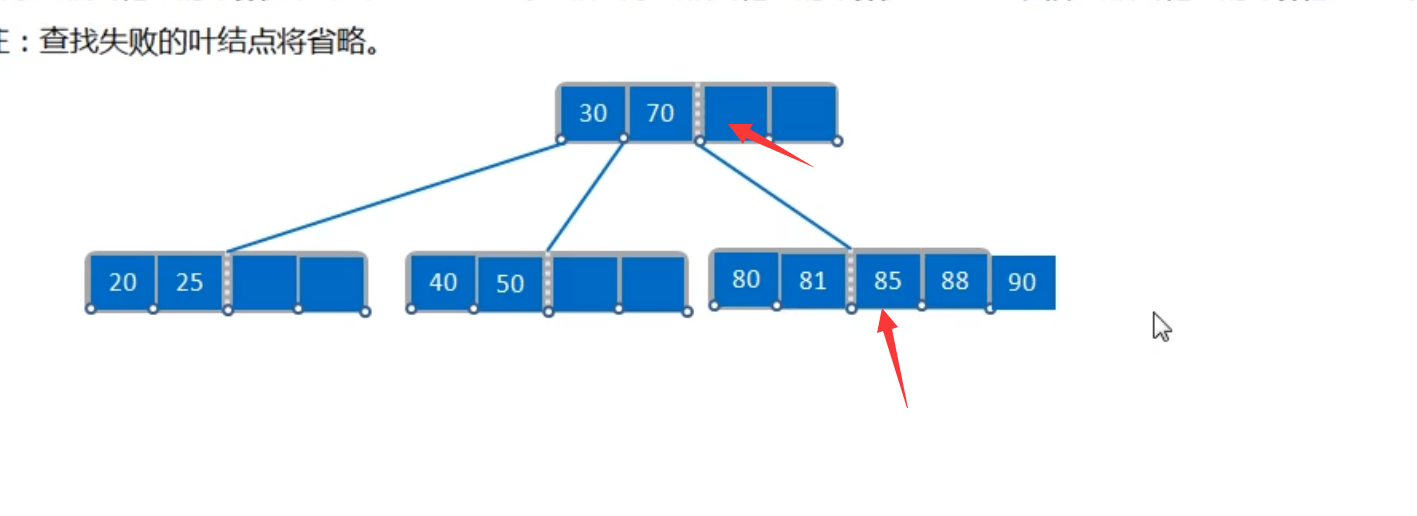

B树删除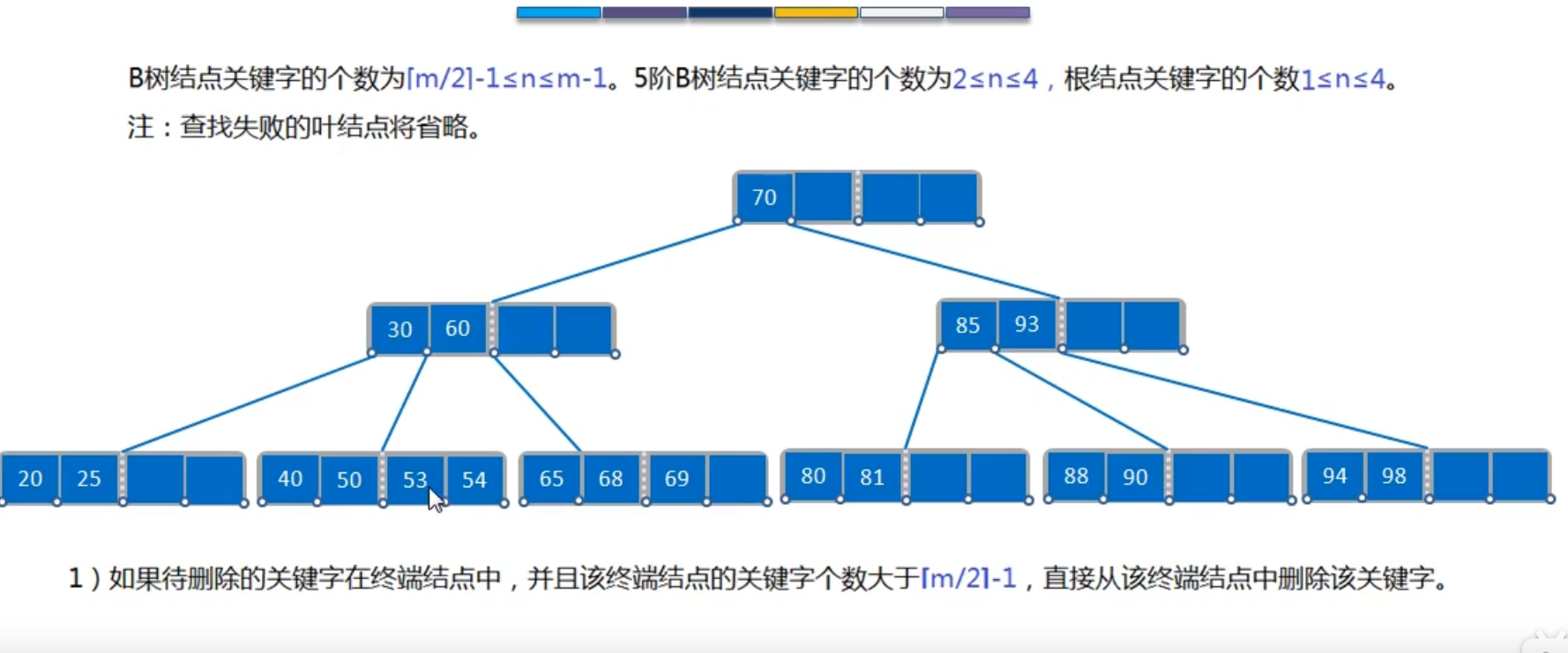



b+树