二叉树

数

1.1 树的性质

（1）子树是不相交的
（2）除了根结点外，每个结点有且只有一个父结点
（3）一颗N个结点的树有N-1条边

1.2 树的基本术语：

（1）结点的度（Degree):结点的子树个数
（2）树的度：树的所有结点中最大的度数
（3）叶结点（Leaf):度为0的结点
（4）父结点（Parent）:有子树的结点是其子树的根结点的夫结点
（5）子节点（Child）：若A结点是B结点的父结点，则称B是A的子结点，也称孩子结点
（6）兄弟结点（Sibling):具有同一父结点的各结点
（7）结点的层次（level）：根节点在1层，其他任一结点层数是其父结点层数加1
（8）树的深度（Depth):树中所有结点中的最大层次
（9）祖先结点（Ancestor）
（10）子孙结点（Descendant）
（11）路径和路径长度

2 二叉树

每个结点最多只有两个子树的树结构，称为左子树（left subtree)和右子树（right subtree)

2.1 二叉树的类型

• 完全二叉树：若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子节点，并且叶子结点都是从左到右依次排布。
• 满二叉树：除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
• 平衡二叉树：又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

2.2 二叉树的性质

• 一个二叉树第i层的最大结点数为
• 深度为k的二叉树有最大结点总数为
• 对任何非空二叉树T,若表示叶结点的个数，表示度为2的非叶结点个数，那么
• 具有n个结点的完全二叉树的深度为(表示不大于的最大整数)

2.3 二叉树的存储

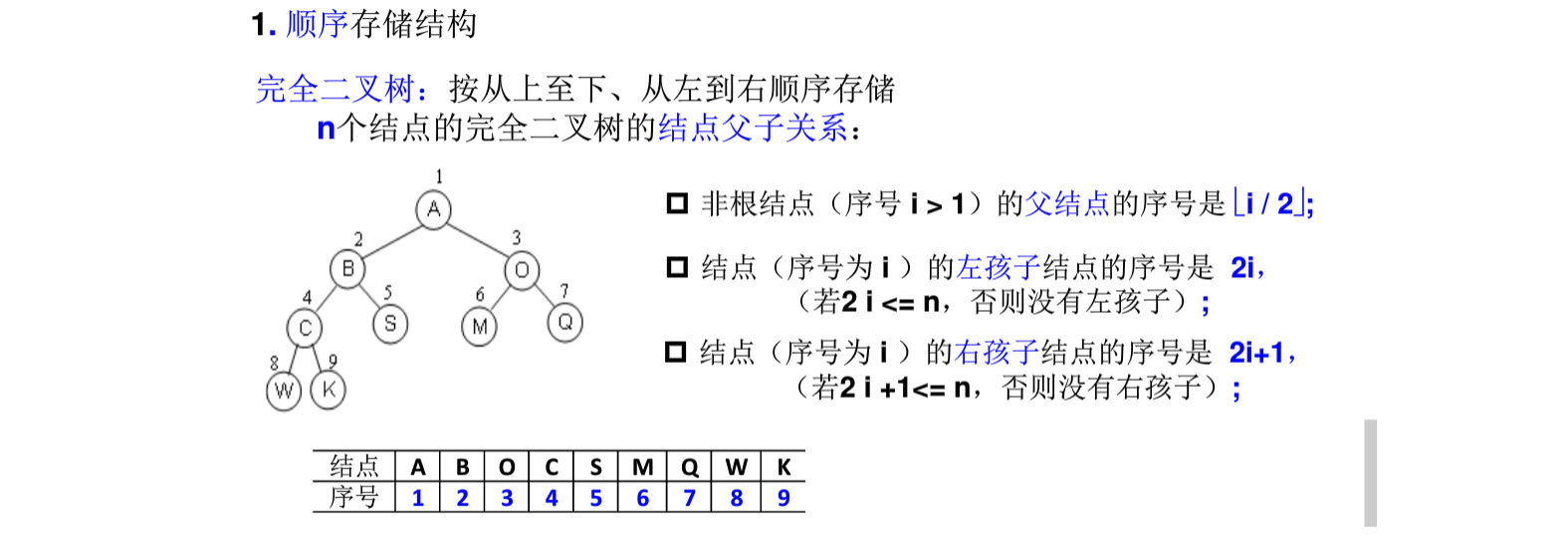
顺序存储结构一般只用于完全二叉树，对于一颗深度为的二叉树，需要分配个存储单元，若用于一般二叉树，会造成对存储空间的浪费

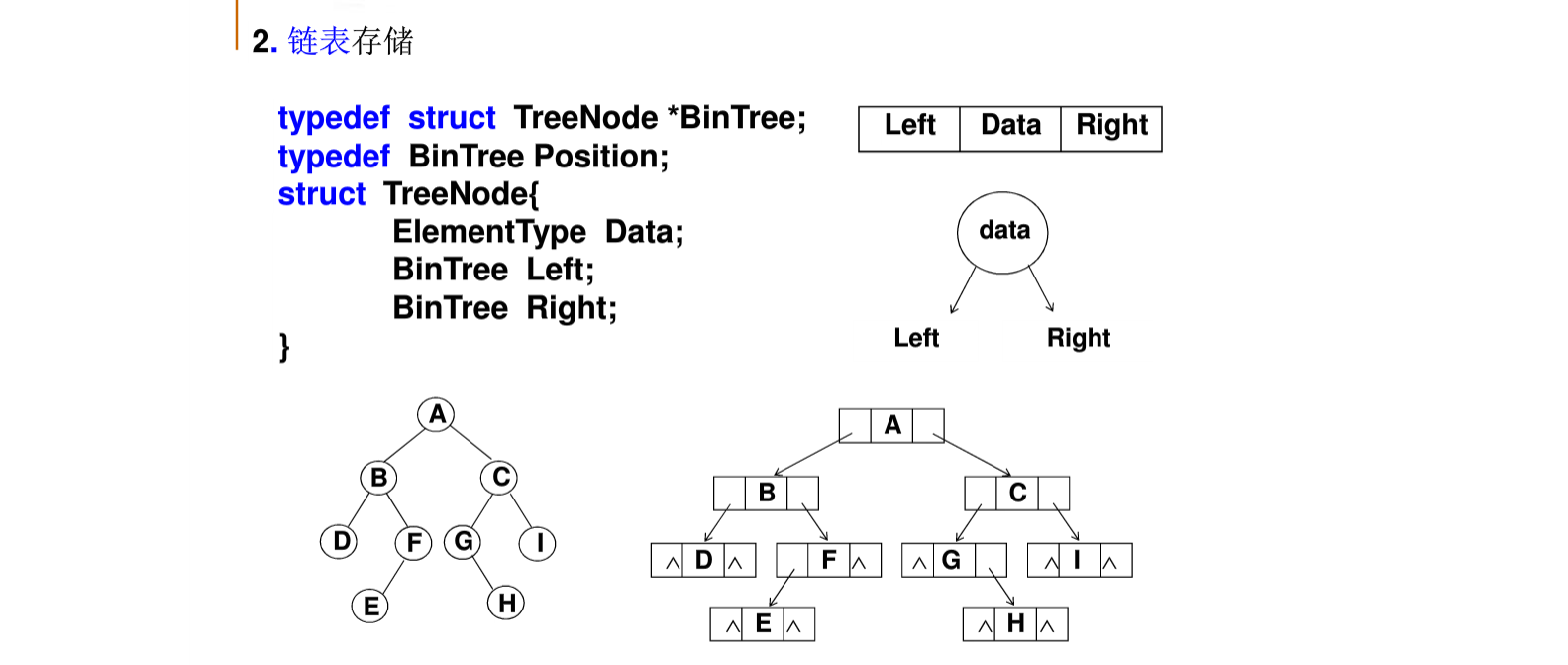
二叉树与树的区别:
（1） 树中结点的最大度数没有限制，而二叉树结点的最大度数为2

（2） 树的结点无左、右之分，而二叉树的结点有左、右之分

2.4 二叉树的遍历

以下图二叉树为例进行遍历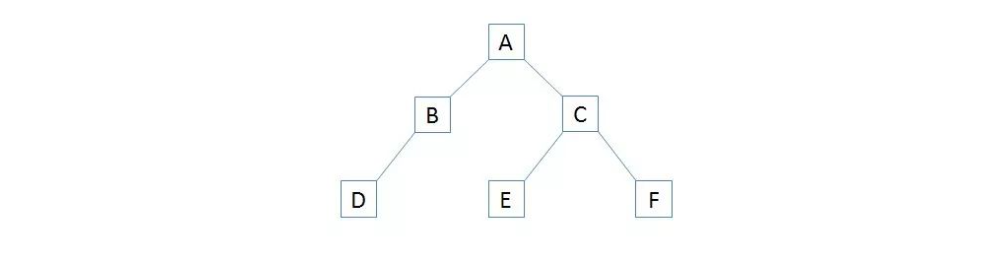

(1)前序遍历

先访问树的根节点，再以类似方式分别遍历左子树和右子树。

遍历顺序：ABDCEF

(2)中序遍历

先遍历左子树，再访问根节点，最后遍历右子树，这个算法先尽量地移动到树的最左边。

遍历顺序：DBAECF

(3)后序遍历

先遍历左子树，再遍历右子树，最后访问根节点。

遍历顺序：DBEFCA

(4)层序遍历

先从0层级开始，在每一个层级按照从左到右的顺序访问节点。

遍历顺序：ABCDEF

Python 实现
代码参考：https://www.cnblogs.com/PrettyTom/p/6677993.html

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
class Tree:
    def __init__(self):
        self.root = None
    def add(self, item):
        node = TreeNode(item)
        if self.root is None:
            self.root = node
        else:
            q = [self.root]
            while True:
                pop_node = q.pop(0)
                if pop_node.left is None:
                    pop_node.left = node
                    return
                elif pop_node.right is None:
                    pop_node.right = node
                    return
                else:
                    q.append(pop_node.left)
                    q.append(pop_node.right)
    # 层序遍历
    def traverse(self):
        if self.root is None:
            return None
        q = [self.root]
        res = []
        while q != []:
            pop_node = q.pop(0)
            res.append(pop_node.val)
            if pop_node.left is not None:
                q.append(pop_node.left)
            if pop_node.right is not None:
                q.append(pop_node.right)
        return res
    # 前序遍历    
    def preorder(self, root):
        if root is None:
            return []
        res = [root.val]
        left_item = self.preorder(root.left)
        right_item = self.preorder(root.right)
        return res + left_item + right_item
    # 中序遍历
    def inorder(self, root):
        if root is None:
            return []
        res = [root.val]
        left_item = self.inorder(root.left)
        right_item = self.inorder(root.right)
        return left_item + res + right_item
    # 后序遍历
    def postorder(self, root):
        if root is None:
            return []
        res = [root.val]
        left_item = self.postorder(root.left)
        right_item = self.postorder(root.right)
        return left_item + right_item + res
t = Tree()
for i in range(10):
    t.add(i)
print('层序遍历:',t.traverse())
print('先序遍历:',t.preorder(t.root))
print('中序遍历:',t.inorder(t.root))
print('后序遍历:',t.postorder(t.root))