码
原码
所谓原码就是二进制定点表示法,即最高位为符号位,“0”表示正,“1”表示负,其余位表示数值的大小。
反码
反码通常是用来由原码求补码或者由补码求原码的过渡码。
正数的反码与其原码相同;
负数的反码:符号位不变,数值位按位去反;
补码
正数的补码与其原码相同;
负数的补码是在其反码的末位加1。
负数通过补码求原码有2种方式:
- 逆推法:补码[末位减1]= 反码;反码[符号位不变,数值位取反] = 原码
- 和原码求补码一样:补码[符号位不变,数值位按位去反,然后整个数加1] = 原码
移码
是一种将全0码映射为最小负值、全1码映射为最大正值的编码方案。移码主要用于表示浮点数的阶码。为什么要使用反码和补码
在开始深入学习前, 我的学习建议是先”死记硬背”上面的原码, 反码和补码的表示方式以及计算方法. 现在我们知道了计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同: [+1] = [00000001]原 = [00000001]反 = [00000001]补 所以不需要过多解释. 但是对于负数: [-1] = [10000001]原= [11111110]反= [11111111]补 可见原码, 反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式, 为何还会有反码和补码呢? 首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (补码的绝对值称为真值即去掉符号位的二进制数字). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别”符号位”显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了. 于是人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码: 计算十进制的表达式: 1-1=0 1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原= [10000010]原 = -2 如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数. 为了解决原码做减法的问题, 出现了反码: 计算十进制的表达式: 1-1=0 1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反+ [1111 1110]反= [1111 1111]反= [1000 0000]原= -0 发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在”0”这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0. 于是补码的出现, 解决了0的符号以及两个编码的问题:
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补+ [1111 1111]补= [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补+ [1000 0001]补= [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].
因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.
浮点数
浮点数的存储模型
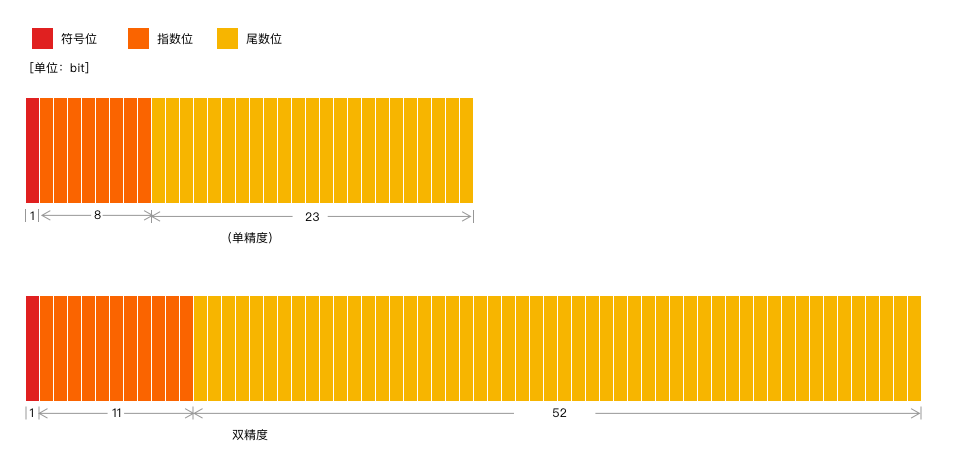
S-sign(符号位) E-exponent(指数) M-mantissa(尾数)
符号位:
只能是0或是1。0表示整数;1:表示负数。
指数位:
指数位又称阶码,表示小数点的位置,采用移码方式来表示。
移码方法对两个指数大小的比较和对阶操作都比较方便,因为阶码域值大者其指数值也大。采用这种方式时,将浮点数的指数真值e 变成阶码E 时,应将指数 e 加上一个固定的偏移量,即 E=e+偏移量
偏移量计算公式:(n表示位数)。比如
单精度的指数位是8,那么偏移量是127;双精度的指数位是11,那么偏移量是1023
尾数位:
为了最大限度提高精确度,可以要求尾数规格化,把尾数处理到大于等于1而小于2的区间内,便可省去前述的“1”。
二进位制:11.101 2^1001 可以规格化为:1.1101 2^1010, 存储的尾数中需要:1101即可; 二进位制:0.00110011 2^-1001 可以规格化为:1.10011 2^-1100, 存储的尾数中需要:10011即可;
浮点数的计算公式:
32位:
64位:
浮点数的加法
1) 0操作数的检查
如果其中之一为0,则没必要再计算
2)对阶
顾名思义就是对齐阶码,使得阶码相同,或者说是小数位对齐。
通过尾数的移位改变指数位的大小来实现对齐。由于尾数的左移会引起最高有位的丢失,造成很大的误差;而尾数右移虽引起最低有效位的丢失,但造成的误差较小,因此,对阶操作规定使 尾数右移,尾数右移后使阶码作相应增加,其数值保持不变。很显然,一个增加后的阶码与另一个相等,所增加的阶码一定是小阶。因此在对阶时,总是使小阶向大阶看齐 ,即小阶的尾数向右移位 ( 相当于小数点左移 ) ,每右移一位,其阶码加 1 ,直到两数的阶码相等为止,
3) 尾数加减计算
有效数位 求和。 不论是加法运算还是减法运算,都按加法进行操作,其方法与定点加减运算完全一样。
4) 结果规格化并进行舍入处理
尾数处理到大于等于1而小于2的区间内
3(10)的二进制科学表示法
3(10)=11(2)=
思考个问题:
x = 0.1; y = -0.2;
那么 x - y; 计算机是怎么处理的呢?
是不是先算出 y 的原码,然后符号位变成0,最后做 0.1 + 0.2计算
参考
原码、反码、补码和移码详解
15 张图带你深入理解浮点数
javascript标准参考教程-数值
十进制小数转化为二进制小数
浮点数的表示中为什么要用移码表示阶码?
JavaScript 浮点数陷阱及解法
Javascript IEEE754标准的浮点数二进制表示、浮点数运算及Js为啥0.1+0.2!=-0.3
JavaScript 里最大的安全的整数为什么是2的53次方减一?
二进制可视化工具
https://babbage.cs.qc.cuny.edu/IEEE-754/

