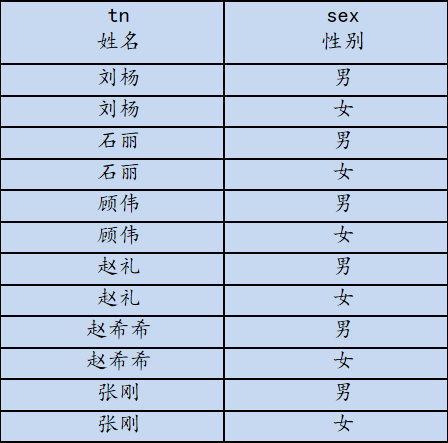
1. 关系的形式化定义

（1）域（Domain）

域是一组具有相同数据类型的值的集合，又称为值域（用D表示）。 例如，整数、实数和字符串的集合都是域。

域中所包含的值的个数称为域的基数（用m表示），例如：
image.png

（2）笛卡尔积（Cartesian Product）

给定一组域D1，D2，…，Dn（它们包含的元素可以完全不同，也可以部分或全部相同），其笛卡尔积为：
D1×D2×…×Dn={（d1，d2，…，dn）|di∈Di，i=1，2，…，n}

每一个元素（d1，d2，…，dn）中的每一个值di叫做一个分量（Component），分量来自相应的域（di∈Di） 每一个元素（d1，d2，…，dn）叫做一个n元组（n-Tuple），简称元组（Tuple）。但元组是有序的，相同分量di的不同排序所构成的元组不同。如，以下三个元组是不同的，（1，2，3）≠（2，3，1）≠（1，3，2）

image.png

若Di（i=1，2，…，n）为有限集，Di中的集合元素个数称为Di的基数，用mi（i=1，2，…，n）表示，则笛卡尔积D1×D2×…×Dn的基数M（即元组（d1，d2，…，dn）的个数）为所有域的基数的累乘之积

image.png

笛卡尔积可用二维表的形式表示，例如，笛卡尔积D1×D2的二维表形式为

image.png

（3）关系（Relation）

D1×D2×…×Dn的有限子集称为在域D1, D2, …, Dn上的关系，表示为 ： r(D1, D2, …, Dn) 其中，r表示关系的名字，n是关系的目或度(degree)。当 n=1时，该关系称为单元关系；当n=2时，称为二元关系。 关系是笛卡尔积的有限子集，所以关系也是一个二维表, 表的每行对应于关系的一个元组，表的每列对应于关系的一个域。 由于域可以相同，为了区别就必须给每列起一个名字，称为属性(attribute)。n目关系共有n个属性。

空值(null)是所有可能的域的一个取值，表明值未知或值不存在。

  • 对于学位的取值域，某员工的学位为空值null，表示不知道该员工所获得的学位，或该员工没有获得学位；
  • 对于成绩的取值域，某学生的成绩为空值null，表示不知道该学生的成绩，或该学生没有成绩(如没有参加考试就没有获得成绩)。

关系的最基本要求：

  • 关系中的每个属性的域必须是原子的，即域中的每个值都是不可再分的一个完整单元。
  • 关系中的每个元组都是可区分的，即存在唯一标识不同元组的属性(集)——码。

关系的几点说明： （1）在关系R中，当n=1时，称为单元关系。当n=2时，称为二元关系，以此类推。 （2）关系中的元组通常用t表示，关系中元组个数是关系的基数。 （3）关系中的不同域（列）的取值可以相同，为了加以区别，必须对每个域（列）起一个名字，称为属性（Attribute），n元关系必有n个属性，属性的名字唯一；属性的取值范围称为值域，等价于对应域Di（i=1，2，…，n）的取值范围。具有相同关系框架的关系称为同类关系。 （4）在数学上，关系是笛卡尔积的任意子集，但在实际应用中，关系是笛卡尔积中所取的有意义的子集。

定义在域D1，D2，…，Dn（不要求完全相异）上的关系由关系头（Heading）和关系体（Body）组成。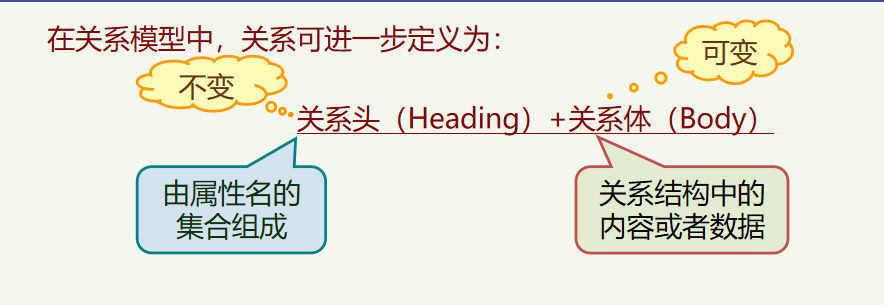
image.png

2.关系的性质

  • 列是同质的，即每一列中的分量必须来自同一个域，必须是同一类型的数据。
  • 不同的属性可来自同一个域，但不同的属性必须有不同的名字。例如，假设某关系中的两个属性“职业”和“兼职”，它们可以来自同一个域{教师，工人，辅导员}。
  • 列的顺序可以任意交换。但交换时，应连同属性名一起交换，否则将得到不同的关系。
  • 关系中元组的顺序（即行序）可任意，在一个关系中可以任意交换两行的次序。因为关系是以元组为元素的集合，而集合中的元素是无序的，所以作为集合元素的元组也是无序的。
  • 关系中不允许出现相同的元组。因为数学上集合中没有相同的元素，而关系是元组的集合，所以作为集合元素的元组应该是唯一的。
  • 关系中每一分量必须是不可分的数据项，也就是说，不能出现“表中有表”的现象。满足此条件的关系称为规范化关系，否则称为非规范化关系。

例如，以下左表是非规范化关系，可以把其中的属性“籍贯” 分成两个新的属性，即“省（区市）” 、“市/县” ，将其规范化，如右表所示。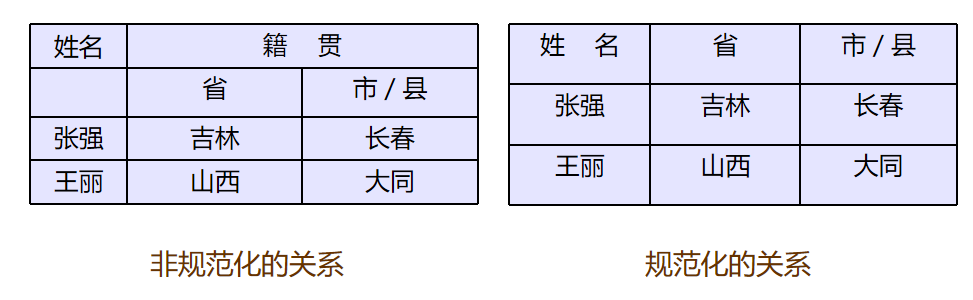
image.png

3. 关系的分类

image.png