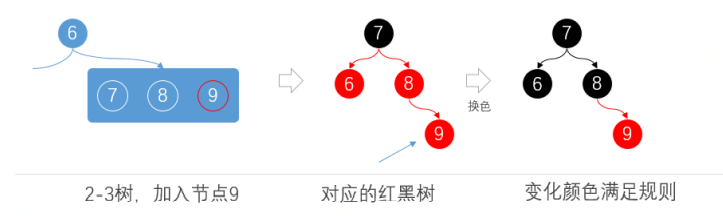
2-3树

2-3树是一种有两种节点的平衡树：2节点和3节点

• 2节点有一个数据和两个孩子
• 3节点有两个数据和三个孩子

对于一颗平衡的2-3树来说，所有的空链接（叶节点）都和根节点的距离相同。
同时还有如下重要性质：

• 1 个节点 1 个数据时，则有两个子节点 ，左孩子值小于数据值，右孩子大于数据值

• 1 个节点 2 个数据时，则有三个子节点，且中间子节点是介于两个节点间的值

  插入

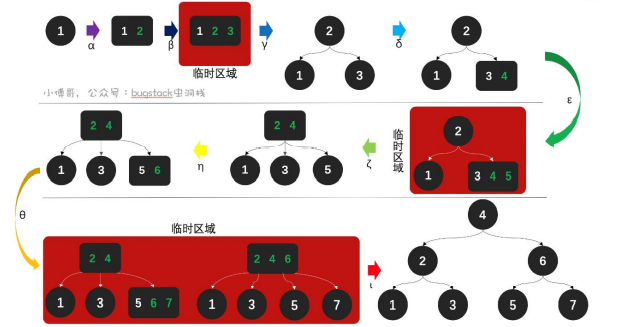
  2-3树的插入操作规则如下：

• 如果插入的数据和2节点比较，则直接插入进2节点中变成3节点

• 如果插入的数据和3节点比较，则将3节点替换成一个2节点和两个孩子2节点
• 如果插入的数据的3节点有父节点2节点，且插入会破坏性质，则向上调整将父节点变为3节点
• 如果插入的数据的3节点有父节点3节点，且插入会破坏性质，则先将父节点临时扩充为4个数据元素的节点，然后按顺序全部拆分成3层的树

删除

2-3树的删除规则如下：

• 如果删除的节点是3节点的元素，则可以直接删除
• 如果删除的节点是2节点，则需要重新调整树

调整树实际就是先将单边的不平衡调整，即将2节点构成的树化为3节点，然后再整体调整平衡

查找

查找的步骤很简单，就是逐个比较，大于数值就向右，小于就向左。

红黑树

红黑树是一种高效的自平衡查找树，具有良好的效率，可在的时间复杂度下完成插入删除查找等操作。
实际上来说，红黑树是2-3树在代码上实现的一种表现形式，保留了2-3树的低复杂度特性同时又便于实现。其转换关系如下：

1. 2-叉节点，转换比较简单，只是把原有节点转换为黑色节点
2. 3-叉节点，包括了 2 个元素，先用红色线把两个节点相连，之后拆分出来，最后调整高度黑色节点在上
3. 4-叉节点，包括了 3 个元素，分别用红黑线连接，之后拆分出来拉升高度。这个拉升过程和2-3树调整一致，只是添加了颜色

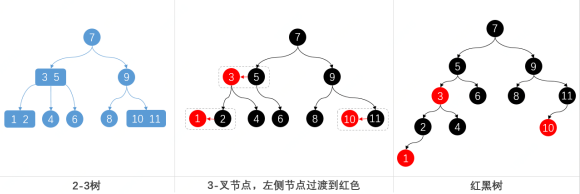
转换后的树满足红黑树的条件：

1. 从任意节点到叶子节点，所经过的黑色节点数目相同
2. 黑色节点保持着整体的平衡性，也就是让整个红黑树接近于时间复杂度
3. 其他红黑树的特点也都满足，可以对照红黑树的特性进行比对

   平衡操作

   为了让红黑树在插入节点后保持平衡性，我们需要进行染色、左右旋转的操作。

   左旋转

   把一个向右倾斜的红节点链接(2-3树，3-叉双元素节点)，转化为左链接。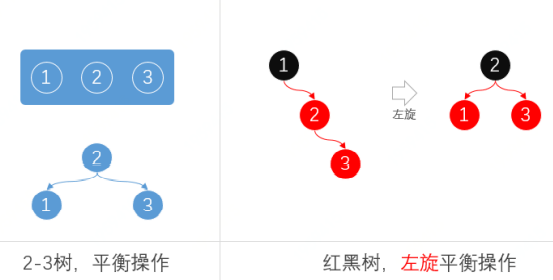
   
   这一个步骤实际上和2-3树的平衡是一样的，因为我们可以把红节点看为黑节点的附属节点，这样的右倾的红节点链接就相当于4节点，需要再平衡。

   右旋转

   把一个向左倾斜的红节点链接(2-3树，3-叉双元素节点)，转化为右链接。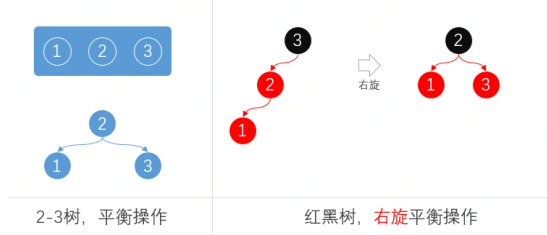
   
   这个操作和左旋对应，容易理解。

   染色

   染色规则单纯说不太好理解，但是结合23树就好懂了，如果因为平衡调整导致出现了超过4的节点，通过染色调整为2节点和3节点。