一、m文件定义函数（m-函数）

Matlab函数的基本结构

在这里必须注意函数脚本名字要与函数名一致
你可以定义一个由自己想要功能的函数，以下是简单的规则：

• 函数代码块以 function关键词开头，后接输出变量和函数标识符名称和圆括号 ()。
• 任何传入参数和自变量必须放在圆括号中间，圆括号之间可以用于定义参数。
• 函数的第一行语句可以选择性地使用文档字符串—用于存放函数说明。
• 函数内容以end结束。

函数需要定义在脚本文件（*.m）中运行，不可以在命令窗口中临时创建。

function[输出形参表: output1, ...,outptn] = 函数名(输入形参表: input1, ... , inputn)
% 注释说明部分
函数体代码部分
end

函数调用

定义完的函数保存为同函数名的m文件，放置在Matlab的当前路径之下（或修改当前路径为m-函数文件所在路径），然后就和使用Matlab自带的函数一样，直接在命令窗口或程序代码中使用该函数就是调用它了。调用函数时，只需要知道函数是完成什么功能的，以及它的输入参数、输出参数。
函数调用的一般格式为：

[输出实参表]=函数名(输入实参表)

注1：函数中遇return语句时，将退出函数体，此函数调用结束；

注2：函数体里面也可以定义一个或几个函数，称为子函数；注意：子函数只能存在于主函数体内，不独立存在；子函数在主函数体内的位置可以任意，不影响使用；子函数只能被主函数以及其他位于同一主函数体下的子函数调用，但子函数“句柄”例外；

注3：在调用函数时，Matlab用两个永久变量nargin和nargout分别记录调用该函数时的输入实参和输出实参的个数。只要在函数文件中包含这两个变量，就可以准确地知道该函数文件被调用时的输入输出参数个数，从而决定函数如何进行处理。

实例

调用的是函数所在文件名，而非函数名,所以尽量让两者一致；
function 首字母小写；
需要注意的是调用函数要在当前文件夹中；

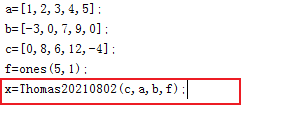
function x=Thomas(c,a,b,f)
%用追赶法求线性方程组 Ax=b的解，其中A为三对角矩阵 A=(c,a,b)
% a为主对角元素向量，b为上对角元素向量，c为下对角元素向量
% (为了算法简便，令abc三向量的元素数相同，c(1) b(n) 多的元素并未参与运算)
%原理  Ax=LUx=Ly=f  先求y向量，再求x向量
n=length(a)

for i=1:n
    if(a(i)==0)
        disp('Error : 对角有元素为0!');
        return;
    end
end

%求解Ly=f的解，解保存在y中
% l(i)=c(i)/u(i-1); 省略一个中间变量
y(1)=f(1)  %y1=f1
u(1)=a(1)
for i=2:n 
    u(i)=a(i)-(c(i)/u(i-1))*b(i-1);
    y(i)=f(i)-(c(i)/u(i-1))*y(i-1);    
end

%求解Ux=y的解 x 
x(n)=y(n)/u(n)
for i=n-1:-1:1
    x(i)=(y(i)-b(i)*x(i+1))/u(i)
end

二、内联函数

可以让用户编写简单的函数而不需要创建M文件。语法格式：
f=inline(‘函数表达式’, ‘变量1’, ‘变量2’, ……)
调用方式：y=f(实参列表)
注意：实参列表顺序应与inline()定义中形参列表的顺序一致。
这种函数定义方式是将它作为一个内部函数调用。好处是，它是基于Matlab的数值运算内核的，所以它的运算速度较快，程序效率更高。缺点是，该方法只能对数值进行代入，不支持符号代入，且对定义后的函数不能进行求导等符号运算。

实例：

f=inline('x^2+y','x','y');
z=f(2,3);

>>z=7

Meshgrid

1、主要使用的函数为[X,Y]=meshgrid(xgv,ygv);

meshgrid函数生成的X，Y是大小相等的矩阵，xgv，ygv是两个网格矢量，xgv，ygv都是行向量。

X：通过将xgv复制length(ygv)行（严格意义上是length(ygv)-1行）得到。 X:将xgv行向量复制到多行

Y：首先对ygv进行转置得到ygv’，将ygv’复制（length(xgv)-1）次得到。Y:将ygv转为列向量并复制到多列

xgv=1:3;
ygv=10:14;
xgv=
    1 2 3  %1*3的行向量
ygv=
    10 11 12 13 14   %1*5的行向量
[X,Y] = meshgrid(xgv,ygv);
X =

     1     2     3
     1     2     3
     1     2     3
     1     2     3
     1     2     3


Y =

    10    10    10
    11    11    11
    12    12    12
    13    13    13
    14    14    14