矩阵运算

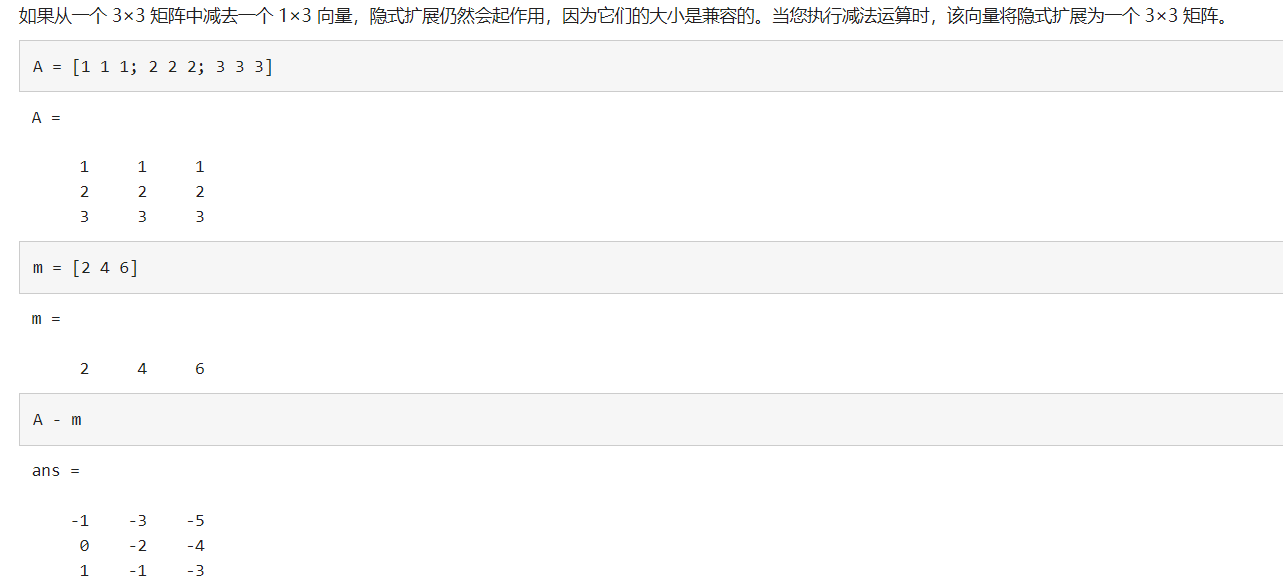
Meshgrid

[b,a]=meshgrid(yita,kexi)=meshgrid(列数，行数）;基于向量 x 和 y 中包含的坐标返回二维网格坐标。a 是一个矩阵，每一列是kexi的一个副本；b也是一个矩阵，每一行是 yita的一个副本。坐标 X 和 Y 表示的网格有 length(kexi) 个行和 length(yita) 个列。

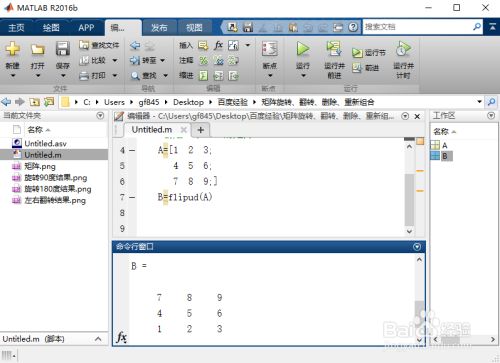
矩阵翻转

flip 翻转矩阵元素

B = flip(A,dim) 沿维度 dim 反转 A 中元素的顺序。
例如，如果 A 为矩阵，flip(A,1) 将反转每一列中的元素，相当于从上向下翻转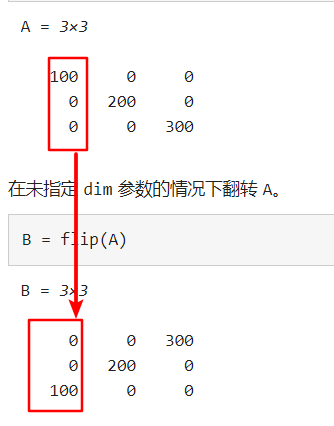

flip(A,2) 将反转每一行中的元素。相当于从右向左翻转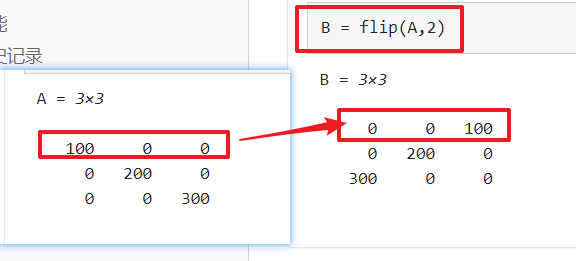

矩阵左右翻转

fliplr()函数将 数组从左向右翻转，具体操作为
B=fliplr(A)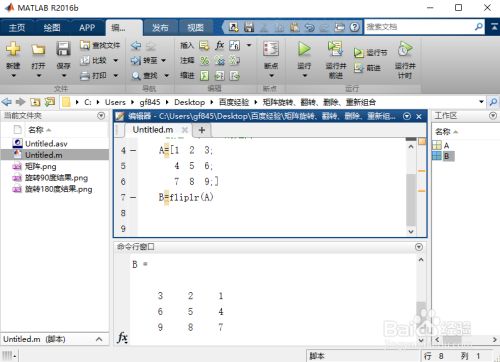

矩阵上下翻转

对矩阵A进行上下翻转操作
B=flipud(A)

生成行向量

方法一：yita=(0:1/12pi:2pi); 等差数列 [0,2π],间隔为1/12*π
方法二： kexi=linspace(0.1,2.5,25); 等差数列 [0.1,2.5],差值为0.1

生成列向量

方法一：a=[1;2;3;4;5]
方法二: b=a’ 先生成行向量，再转制

A=[row1;row2;row3;row4] ；将行隔开 ，隔开列

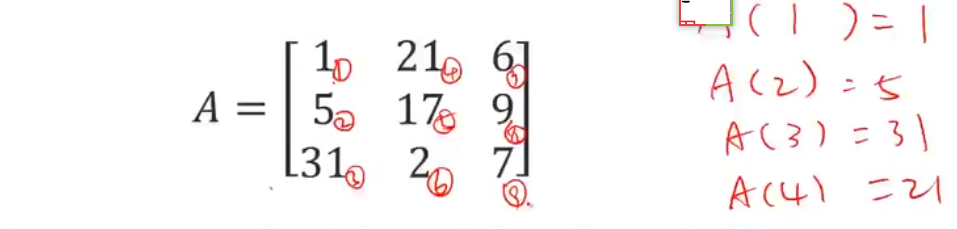
获取矩阵元素

• b(8)=6 访问第8个元素
• b([1 3 5])= 1 11 5 访问第1个、第三个、第五个元素
• b([1 3;4 6])= 1 11 新成立的矩阵，第一行为 b的第一个和第三个元素
• 2 12 第二行为 b的第四个和第六个元素
• b([1 3],[1 3])= 1 3
• 11 13

生成特殊矩阵

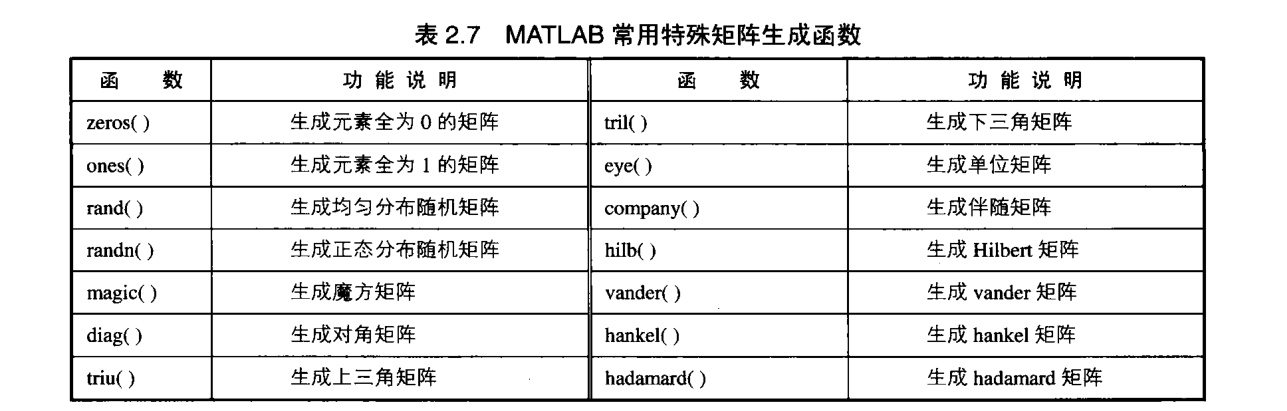
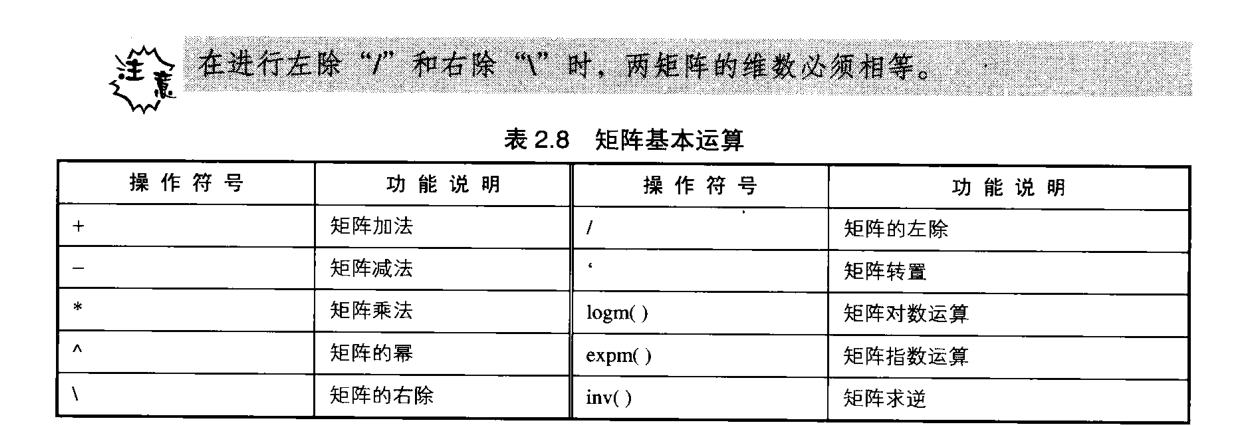
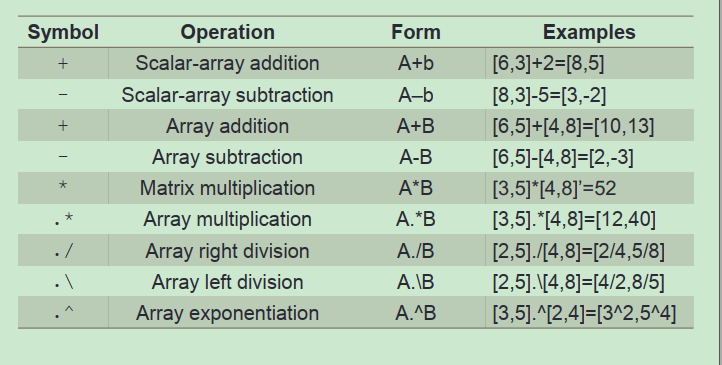
矩阵基础运算

标量与矩阵相乘

矩阵与矩阵相减

矩阵与矩阵/数比较大小

a=[1;2;3];
if a<2
a=[2;3;4];
end

对角矩阵函数 diag

D = diag(v) 返回包含主对角线上向量 v 的元素的对角矩阵。
D = diag(v,k) 将向量 v 的元素放置在第 k 条对角线上。k=0 表示主对角线，k>0 位于主对角线上方，k<0 位于主对角线下方。
x = diag(A) 返回 A 的主对角线元素的列向量。
x = diag(A,k) 返回 A 的第 k 条对角线上元素的列向量。
总结：把向量变成矩阵，把矩阵变成向量

实例

v=[2 1 -1 -2 -5];

d=diag(v);% D = diag(v) d= 2 0 0 0 0 0 1 0 0 0 0 0 -1 0 0 0 0 0 -2 0 0 0 0 0 -5

e=diag(v,1); % D = diag(v,k) e= 0 2 0 0 0 0 0 0 1 0 0 0 0 0 0 -1 0 0 0 0 0 0 -2 0 0 0 0 0 0 -5 0 0 0 0 0 0

h=diag(ones(4,1),-1)

h =

 0     0     0     0     0
 1     0     0     0     0
 0     1     0     0     0
 0     0     1     0     0
 0     0     0     1     0

a=randi(10,6);%随机生成 矩阵元素都不大于10,6*6阶矩阵

x=diag(a); %x = diag(A)

x= 10

10

2

9

2

7

y=diag(a,-1) %x = diag(A,k)

y =

2

10

5

10

8

矩阵函数

size（A） 返回n行m列
length（A）返回向量的长度（矩阵则是n,m中的最大值）

mesh画图

这个老爷子写这个程序的时候就没变换坐标，x轴方向向右，y轴方向向上，所以造成了很大的困扰给人。
如果变化坐标了，写代码会容易的多！！！