定义与实例

Queue 是先进先出的队列，而 PriorityQueue 是优先级队列，其在执行 poll()/remove() 时，会优先取出权重最小的值，它的权重指的是元素的大小，有两种实现方式

1. 通过构造方法里传入 Comparator 的实现
2. 通过元素本身实现的 Comparator 接口

如果两个实现都没有的话，则退化为先进先出队列，下面就先来个例子

Queue<Integer> queue = new PriorityQueue<>();
queue.offer(3);
queue.offer(5);
queue.offer(10);
queue.offer(7);
queue.offer(4);
int size = queue.size();
for (int i = 0; i < size; i++) {
    System.out.println(queue.poll());
}
// 输出
3
4
5
7
10

深入理解

数据结构

PriorityQueue 内部的数据结构是一个实现了二叉堆算法的数组（小顶堆，任意一个非叶子节点的权值，都不大于其左右子节点的权值）

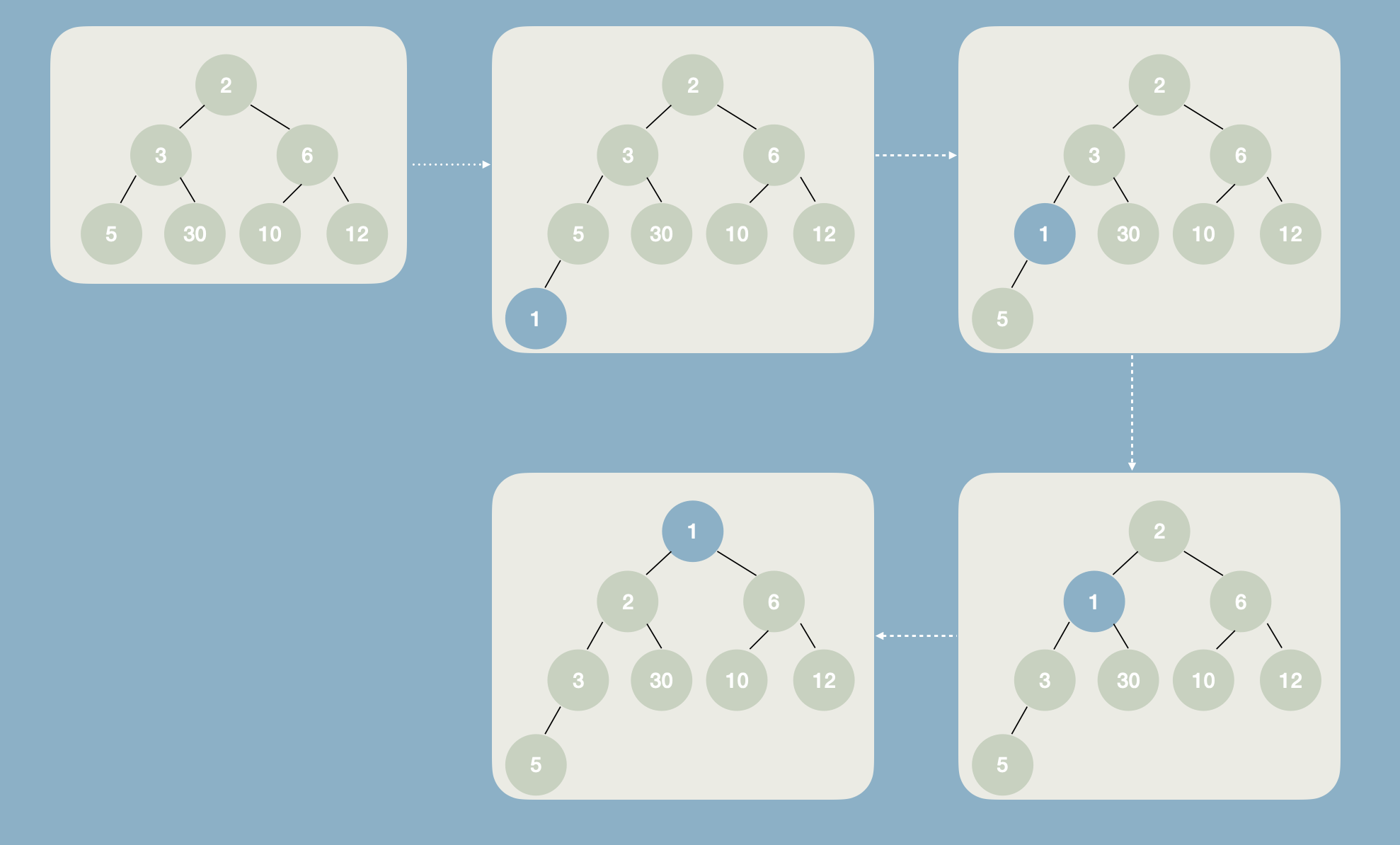
二叉堆： 二叉堆就是完全二叉树，是平衡树的一种，下面举个例子去看下 例如依次插入 3、5、10、2、30、6、12、1 提问：为什么要用完全二叉树呢，用红黑树不香吗？ 答：这是根据使用场景而定的，完全二叉树有个很好的理由就是取最小值的性能是 O(1)

刚刚上边的引用里依次插入了 3、5、10、2、30、6、12、1，那么在 PriorityQueue 中数组存储为

小知识点： 二叉树用数组存储的话，父节点、左节点、右节点公式如下：

• 父节点：(nodeNo-1)/2
• 左节点：(parentNo*2)+1
• 右节点：(parentNo*2)+2

源码方法解析

这章主要是源码解析，涉及到三类

• 入队：add、offer
• 检查：element、peek
• 出队：remove、poll
• 指定删除：remove(Object o)

add 和 offer

在 PriorityQueue 中 add 和 offer 是一致的，add 内部就是调用了 offer，没有任何其他的行为。看 offer 的源码除了扩容外，最主要的就是 siftUpUsingComparator(int insertIndex,E value,Object[] array,Comparator<? super T> cmp) 方法，下面把这段代码复制出来，insertIndex 默认先插入到数组最后

    private static <T> void siftUpUsingComparator(
        int insertIndex, T value, Object[] es, Comparator<? super T> cmp) {
        while (insertIndex > 0) {
            int parent = (insertIndex - 1) >>> 1; // parentNo = (nodeNo-1)/2 获取父节点在数组中的角标
            Object e = es[parent]; 获取父节点的值
            if (cmp.compare(value, (T) e) >= 0) 如果要插入的值大于父节点，则找到了要插入数组角标的值
                break;
            es[insertIndex] = e;否则当前 insertIndex 角标与父节点角标交换（也就是插入节点与父节点交换），然后循环接着与父节点比较
            insertIndex = parent;
        }
        es[insertIndex] = value;
    }

下面用个图去说明下插入流程

element 和 peek

element 和 peek 都是获取首元素但不删除，只是在没有首元素的时候处理的行为有所不同，element 会直接抛出异常而 peek 则返回 null，看源码 element 其实是调用了 peek 的。而 peek 的代码就很简单，就是返回 index 为 0 的数值，如下

    public E peek() {
        return (E) queue[0];
    }

remove 和 poll

remove 和 poll 都是获取并删除首元素，在没有首元素时，remove 会抛出异常而 poll 则返回空，由于 remove 会调用 poll，则下面就主要分析 poll 的代码

    public E poll() {
        final Object[] es;
        final E result;
        if ((result = (E) ((es = queue)[0])) != null) { // 取出头数据
            modCount++;
            final int n;
            final E x = (E) es[(n = --size)]; // 获取最后一个数据
            es[n] = null;
            if (n > 0) {
                final Comparator<? super E> cmp;
                if ((cmp = comparator) == null)
                    siftDownComparable(0, x, es, n);
                else
                    // 第一个参数： 不知道
                    // 第二个参数： 数组最后一个值
                    // 第三个参数： 数组（树）
                    // 第四个参数： 数组长度
                    // 第五个参数： 对比器
                    siftDownUsingComparator(0, x, es, n, cmp);
            }
        }
        return result;
    }

remove(Object o)