力扣上很多树的题目都是可以用递归很快地解决的，而这一系列递归解法中蕴含了一种很强大的递归思维：对称性递归(symmetric recursion)
什么是对称性递归？就是对一个对称的数据结构（这里指二叉树）从整体的对称性思考，把大问题分解成子问题进行递归，即不是单独考虑一部分(比如树的左子树)，而是同时考虑对称的两部分(左右子树)，从而写出对称性的递归代码。

题目分类

image.png

题目解读

image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png

解题模板

下面给出二叉树对称性递归的解题模板

  1. 递归结束条件：特殊情况的判断

如果是单树问题，一般来说只要进行以下判断：

  1. if(!root) return true/false;
  2. if(!root->left) return true/false/递归函数;
  3. if(!root->right) return true/false/递归函数;

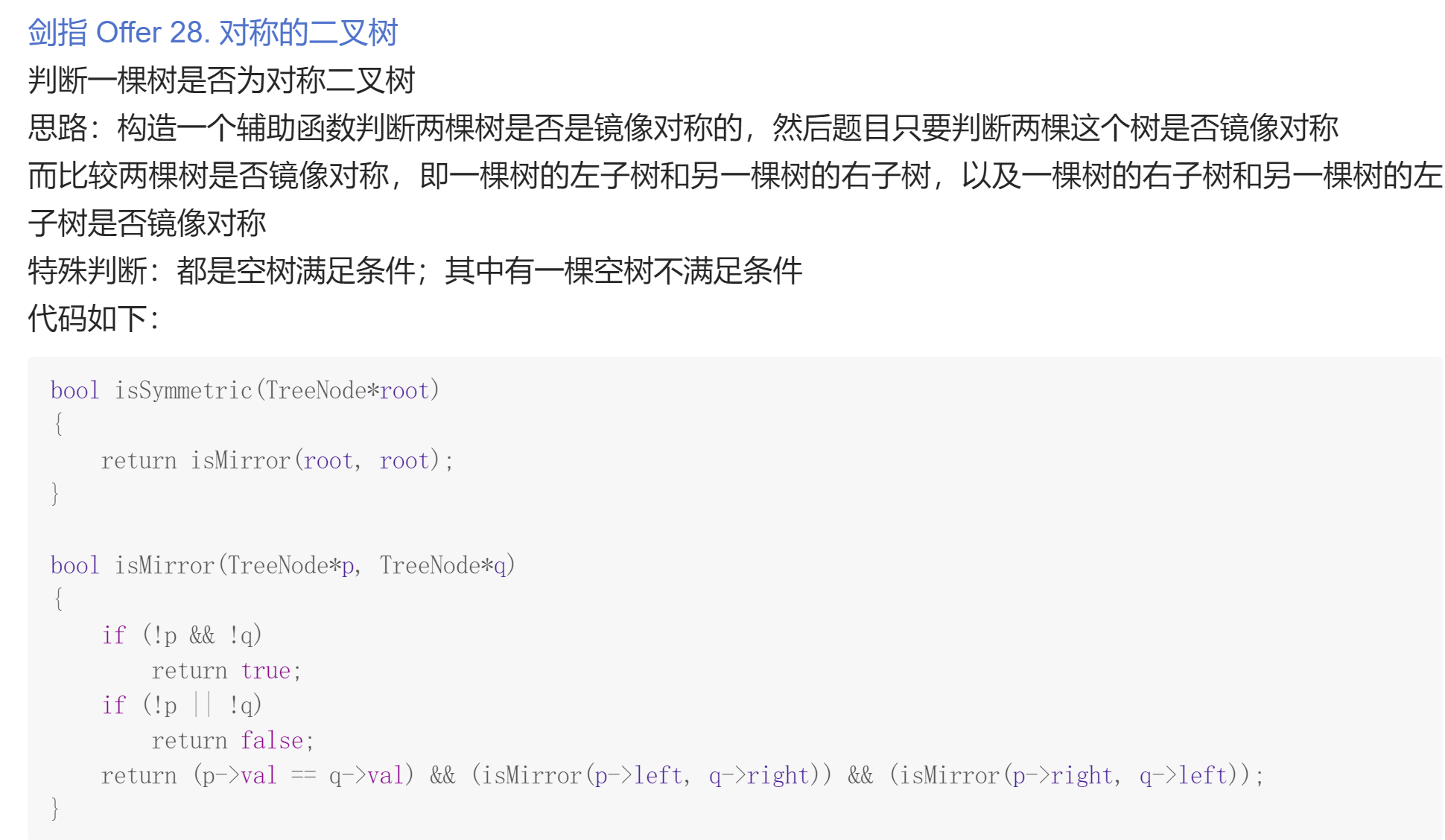
如果是双树问题(根节点分别为p,q)，一般来说进行以下判断：

  1. if(!p && !q) return true/false;
  2. if(!p || !q) return true/false;

当然也不完全是这些情况，比如有的需要加上节点值的判断，需要具体问题需要具体分析

  1. 返回值

通常对称性递归的返回值是多个条件的复合判断语句
可能是以下几种条件判断的组合：
节点非空的判断
节点值比较判断
(单树)调用根节点左右子树的递归函数进行递归判断
(双树)调用两棵树的左右子树的递归函数进行判断