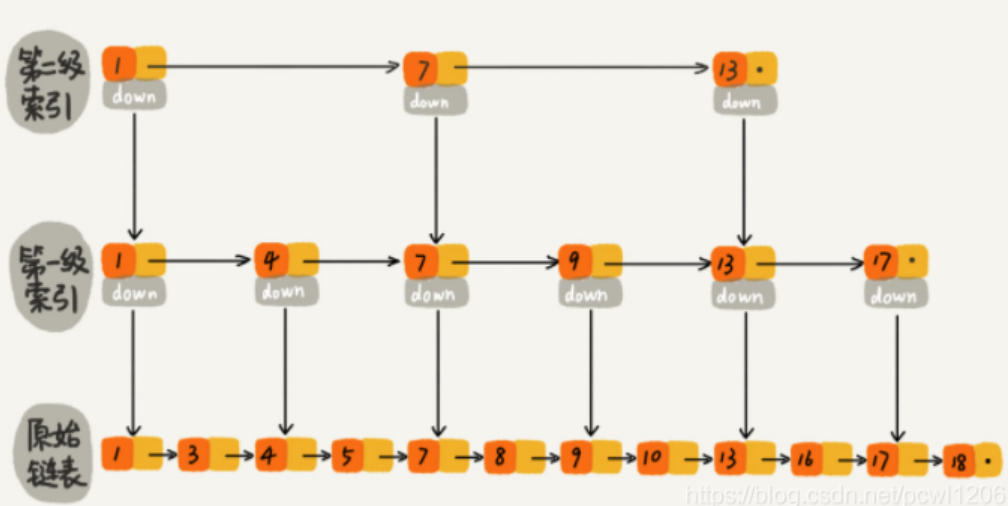
1.Mysql数据在硬盘上的存储形式

Mysql数据在硬盘上是以页的形式存储的。
每个数据页内部是以连续的内存地址存储的行数据
每个数据页之间通过双向指针连接的，最终组成一个双向链表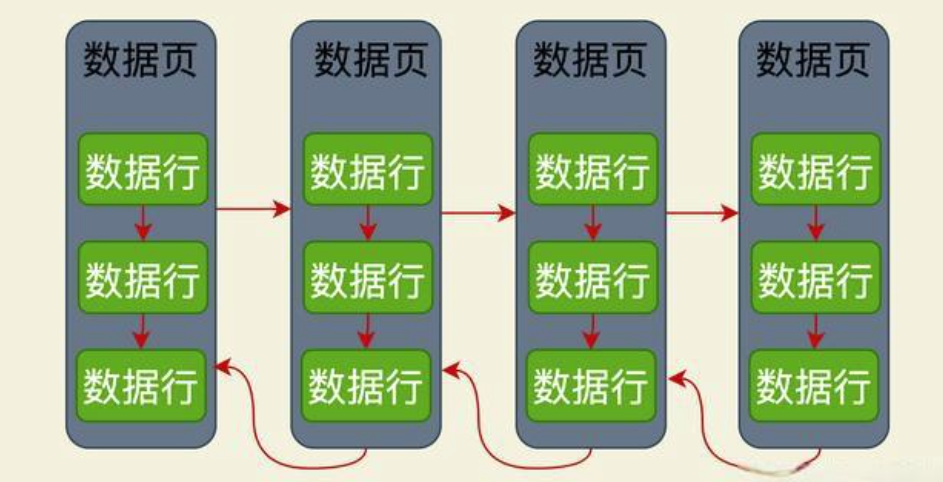
image.png

2.为什么需要索引

根据第一点描述。如果没有索引机制，当等值搜索数据或者范围搜索数据时，需要在遍历整个页链表数据进行查询。那么当数据量过大时，时间复杂度为O(n)带来的时间开销可以说是很大的。
因此需要一种数据结构，可以存储每行数据的一个或多个标志性属性，或者整个行数据，进而实现不用查询页链表，而是查询这种数据结构，得到最小化的范围，来直接获取查询数据。或查询出标志位属性，再去页链表中查询，就可以优化查询效率。
最终这种数据结构也需要存在于磁盘上，因此，设计这种数据结构的要求可以归类为以下几点

  1. 尽可能少的磁盘IO操作
  2. 便于等值查询和范围查询，最好将查询时间复杂度优化为O(logn)
  3. 在数据进行插入和删除时，尽可能减少内存或时间带来的开销

索引应运而生

3.索引为什么不用hash或skipLIst

数据结构分为两种，线性数据结构与非线性数据结构
线性数据结构包括基础的：数组、链表。还包括进阶的Hash、栈，队列，跳表等
根据上述特性

  1. 数组由于不方便插入删除，同时查询复杂地为O(n)。淘汰
  2. 栈由于不方便插入删除，以及等值或批量查询，淘汰
  3. 队列由于不方便插入删除，以及等值或批量查询，淘汰
  4. 链表不方便范围或等值查询，淘汰
  5. 因此只剩下Hash、跳表
  6. Hash在删除和插入时，需要进行hash数组的扩容以及桶链表的新增或移除。效率上不是很高，同时Hash虽然等值查询较快，但是如果作为范围查询，因为元素是散列分部在Hash数组上，因此根本无从实现。所以Hash可以用来实现等值查询索引，但是不适合范围查询索引。

  7. 跳跃表的本质是一个 按照数据从小到大向右排序的单向链表 ，因此在插入和删除节点上的开销比Hash要好。同时跳表支持等值查询以及范围查询。时间复杂度为O(logn)，等同于二分查找。但是因为跳表需要维护多层链表，那么当数据量过大时，会导致跳表层数过高，进而会导致自上而下的IO操作过多，所以不适合

    image.png

    4.索引为什么不用二叉树

    二叉查找树为什么不适合做索引

    二叉查找树不是平衡的二叉树。二叉查找树的规律

  8. 所有左子树节点的值都小于根节点

  9. 所有右子树节点的值都大与根节点

因此可以维护出一个有序的二叉查找树，在查询数据时，时间复杂度为O(logn)。但是因为二叉查找树是不平衡的，因此一旦所有叶子结点的数据都比根节点大或比根节点小，那么二叉查找树也就退化成了一个链表，此时查找时间复杂度为O(n)。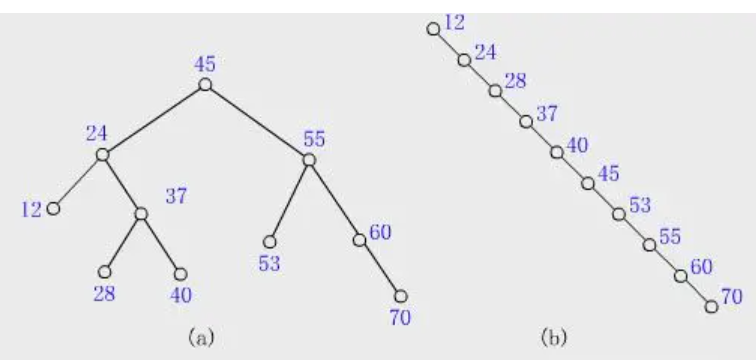
image.png

平衡二叉树为什么不适合做索引

平衡二叉树也遵循二叉查找树的规律，同时由多了一些规律

  1. 所有左子树节点的值都小于根节点
  2. 所有右子树节点的值都大与根节点
  3. 平衡二叉树要么是一棵空树
  4. 要么保证左右子树的高度之差不大于 1
  5. 子树也必须是一颗平衡二叉树

有上述规则可以看出，平衡二叉树不会出现上述链表情况，而是在插入时进行左旋或右旋操作。维护整个树的平衡，同时查询效率也为O(logn)。但是有一个致命问题，因为二叉树的根本在于每个根节点只能有两个子节点，那么当数据量过大时，整个树是纵向延伸的。一旦等值查询的数处于最底层节点，那么带来的硬盘IO次数同样不低

5.B树的缺点

B树具有以下特点

  1. 每个根节点可以有多个叶子结点
  2. 每个节点可以存n个key(value)，同时可以具有n+1个子树
  3. 左子树的所有key的值都比根节点最左key的值小
  4. 右子树的所有key的值都比根节点最右key的值大
  5. 中间子树的所有key的值都介于根节点最左key与最右key的值之间

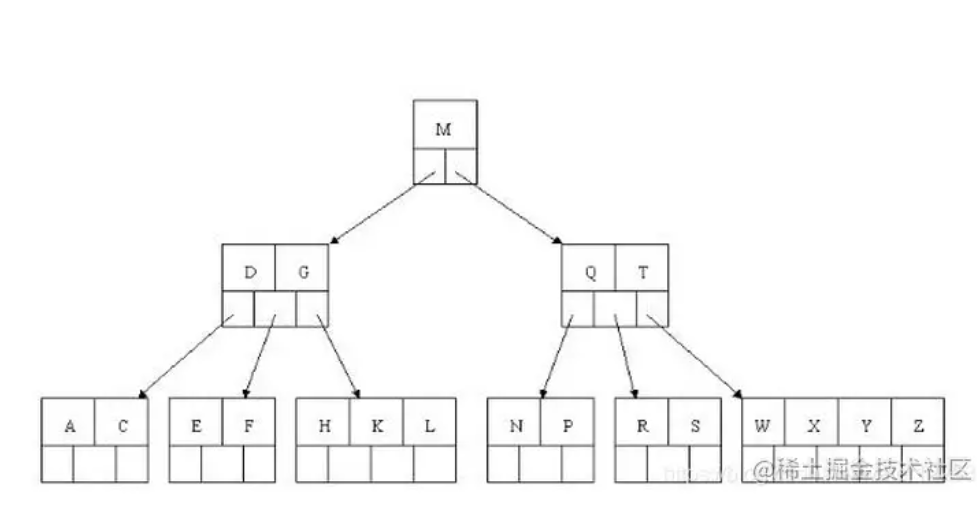
image.png
根据图片可以看出，B数相比较与二叉树，当数据量大时，会进行横向扩展，而不是纵向扩展，同时查询效率也为O(logn)。并且B数在增删数据时，相比较线性数据结构也要好很多。
但是有一个很严重的问题，当范围查询时，以上图为例，当需要查询A~Z的数据时，需要频繁的进行子节点与根节点之间的往返。这也会带来较多的IO操作。这个弊端也是以上所有树结构的通病。

6.B+树为什么适合索引

B+树具有以下特点：

  1. 所有根节点不存value，只存key
  2. 所有的value都存在与根节点中
  3. 根节点之间通过双向指针维护一个双向链表结构
  4. 每个根节点可以有多个叶子结点
  5. 每个根节点可以存n个key，同时可以具有n个子树
  6. 每个根节点的key表示的是子树中的最大key，在子树中同样含有这个key

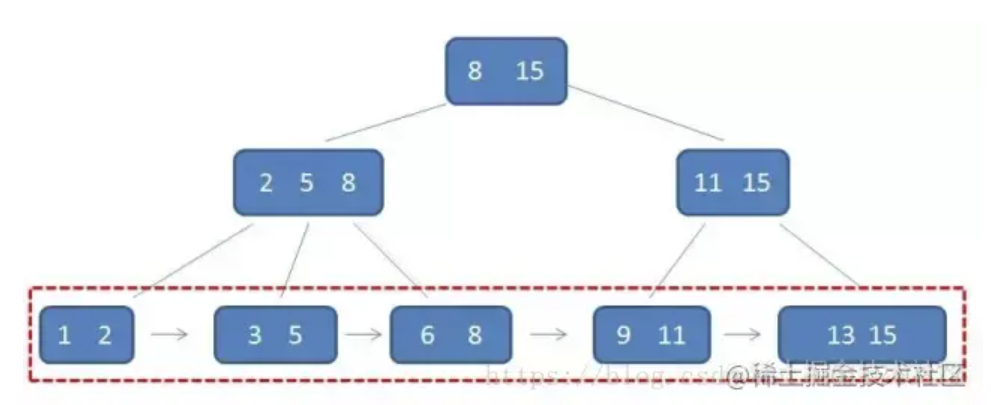
image.png
根据上图可以看出，B+树具有B树同样的大数据量时纵向扩展特性。同时B+树的插入以及删除操作效率高于线性数据结构。并且在等值查询时，B+树的查询效率也等于O(logn)。而且在范围查询上，因为B+的所有叶子结点维护了一个双向链表，因此不用进行父节点的往返，只需定位查询范围的头尾节点，在根节点进行从左到右遍历操作即可。进一步减少了IO操作。综上所述，B+树满足了作为索引的所有条件。因此选择二叉树作为索引的基础数据结构。

7.聚簇索引

聚簇索引可以理解为Mysql根据每个表的主键建立的唯一索引。当没有主键时，自动选择一个非空列建立唯一索引。如果以上两点都不满足，则自动生成一个长度为6个字节的int类型隐藏列创建唯一索引。
聚簇索引具有以下特点：

  1. Innodb中数据类型为B+树
  2. 根节点存储的是主键ID
  3. 叶子结点存储的值是整个行的数据
  4. Innodb的数据存储就是按照聚簇索引来存储的

因此，可以得出以下结论

  1. 主键ID最好自增。因为为了维护聚簇索引（B+树的有序性），一旦主键ID无序，那么可能导致后来的数据插入到之前的数据之中。进而导致索引的维护开销巨大，从而影响性能

    8.非聚簇索引（二级索引）

    单列索引

    在表中单个非主键列建立的索引。具有以下特点：

  2. Innodb中数据结构为B+树

  3. 根节点存储的是非主键列
  4. 叶子结点存储的值是主键ID

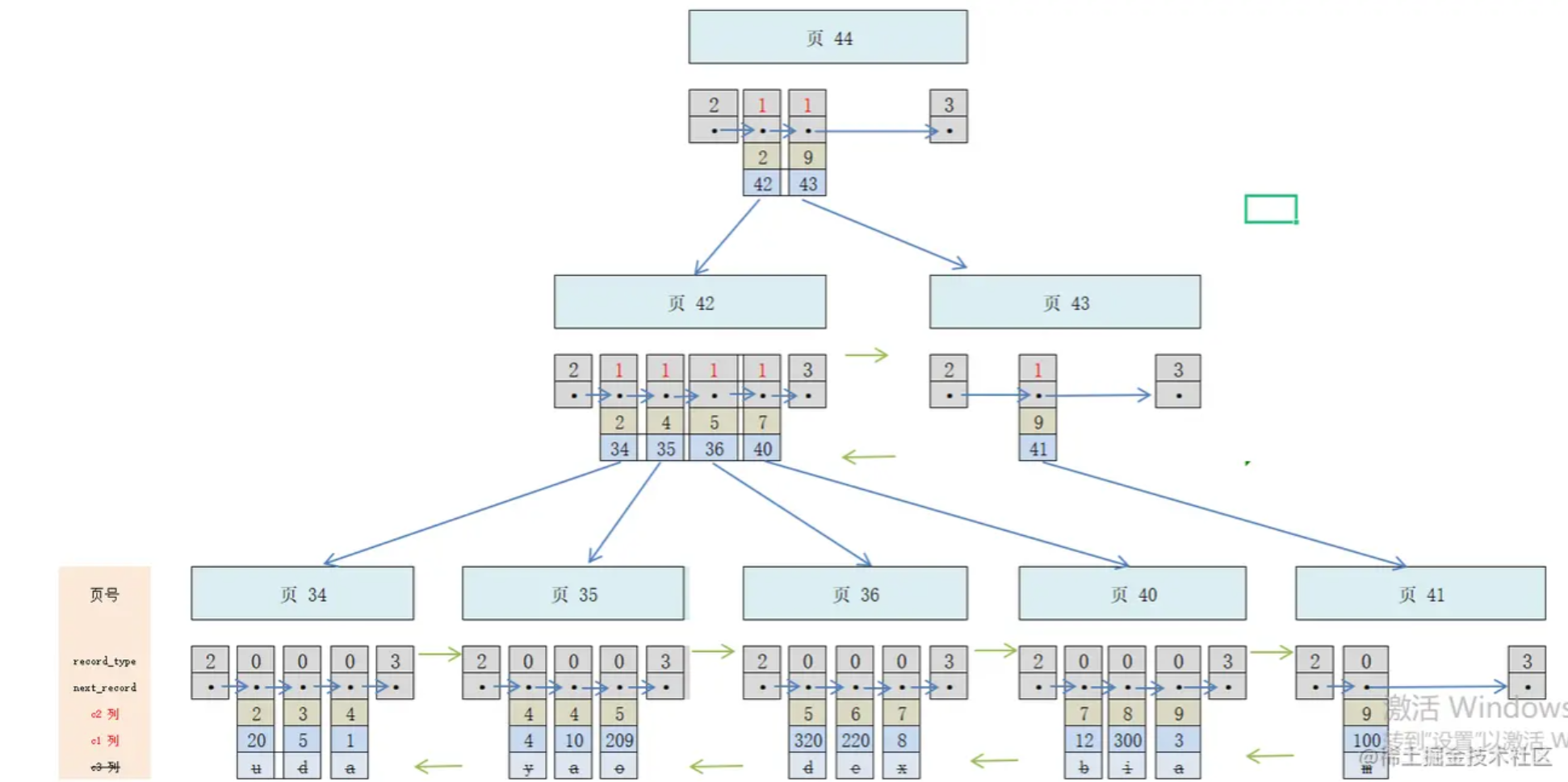
image.png
因此可以得出如下结论

  1. 主键ID占用内存空间小，因为叶子节点最终存储的值是主键ID，如果主键ID过大，会造成不必要的内存浪费。且过多的非聚簇索引会占用过多的内存空间
  2. 查询目标列如果多于或不包括索引列，会先在当前索引B+树中查询到主键ID，进而区查询主键ID索引（聚簇索引），才会得到最终想要的数据。这一过程称之为回表

  3. 查询目标列如果正好匹配索引列，则只需要查询当前索引B+树即可，称之为覆盖索引

    多列索引

    在表中多个非主键列建立的索引。具有以下特点

  4. Innodb中数据结构为B+树

  5. 根节点按照索引列从左到右的顺序 自上而下的存储的是非主键列
  6. 根节点存储非主键列的顺序默认先将最左列排序，然后再最左列相同的情况下，将下一列排序。以此类推
  7. 叶子结点存储的值是主键ID

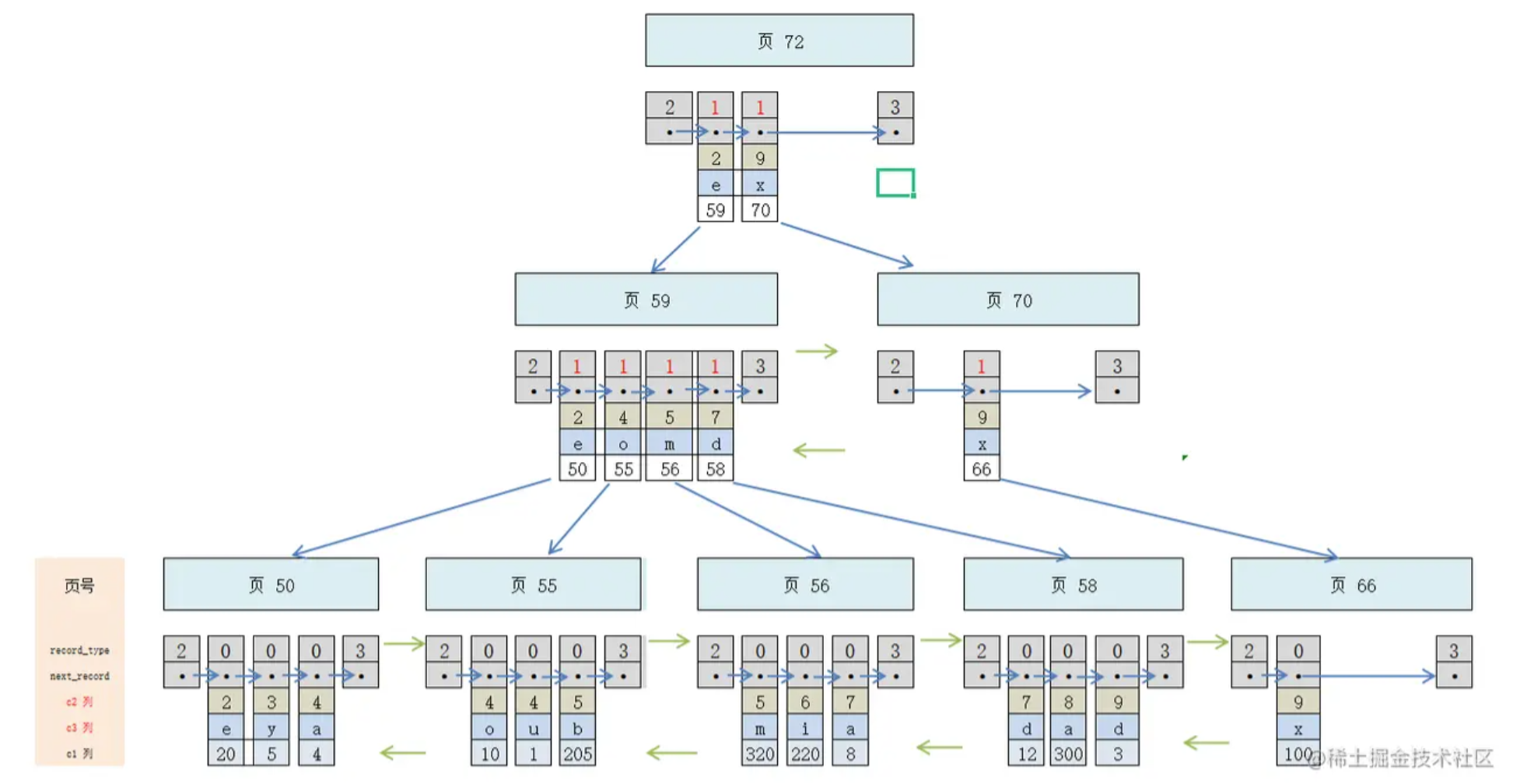
image.png
因此可以得出以下结论：
最左原则：如果在a,b,c列建立联合索引

  • 当查询条件为a=1 and b=1 and c=1 时不用遵循最左原则可忽视顺序，因为mysql的查询优化器会对查询语句进行优化，进而调整回正确的顺序
  • 当查询条件为b=1 and c=1时索引失效。因为可以看出只有当a等值时，b才有序。直接查询b，b不一定有序。
  • 当查询条件为a=1 and b=1 and c<1 时索引abc生效
  • 当查询条件为a=1 and b<1 and c<1 时索引ab生效，c失效

因为联合索引情况下，只有最左列在整个B+树中时有序存放的，其他列都是依赖于上一列的等值而有序存放的，因此其他列整体上并不是有序存放的。
所以最左列无论等值还是范围查找都可以。其他列无法越过上一列进行查找。因为索引的机制就是有序进而实现了二分查找的类似效率。既然已经无序何来二分查找的意义？

9.Mysql的搜索引擎

存储引擎主要有:

  1. InnoDB
  2. MyIsam
  3. Memory
  4. Archive

  5. Federated

    默认为:InnoDB 引擎。InnoDB 底层存储结构为 B+树， B 树的每个节点对应 innodb 的一个 page，page 大小是固定的，一般设为 16k

    10.创建索引的原则

  6. 选择唯一性索引：唯一性索引的值是唯一的。可以更快的通过该索引来确定某条记录。

  7. 为经常需要排序、分组、以及联合查询的列创建索引。
  8. 为经常作为查询条件的列创建索引。
  9. 限制索引的数目：越多的索引越导致表的查询效率变低，因为索引表在每次更新表数据的时候都会重新创建这个表的索引，表的数据越多，索引列越多，那么创建索引的时间消耗就越大。
  10. 如果索引的值很长，那么查询的速度会受到影响。
  11. 如果索引字段的值很长，最好使用值得前缀来进行索引。
  12. 删除不再使用或者很少使用的索引。
  13. 最左前缀匹配原则，非常重要的原则（尽量将匹配度高的列放在最左边）
  14. 尽量选择区分度高的列作为索引.
  15. 索引列不能参与计算，保持列“干净”:带函数的查询不参与索引。

  16. 尽量的扩展索引，不要新建索引。

    11.索引失效的情况

  17. like以%开头索引无效，当like以&结尾，索引有效。

  18. or语句前后没有同时使用索引，当且仅当or语句查询条件的前后列均为索引时，索引生效。
  19. 组合索引，使用的不是第一列索引时候，索引失效，即最左匹配规则。
  20. 数据类型出现隐式转换，如varchar不加单引号的时候可能会自动转换为int类型，这个时候索引失效。
  21. 在索引列上使用IS NULL或者 IS NOT NULL 时候，索引失效，因为索引是不索引空值。
  22. 在索引字段上使用，NOT、 <>、= 、时候是不会使用索引的，对于这样的处理只会进行全表扫描。
  23. 对索引字段进行计算操作，函数操作时不会使用索引。

  24. 当全表扫描速度比索引速度快的时候不会使用索引。

    12.添加索引的语句

  25. 主键索引：ALTER TABLE table_name ADD PRIMARY KEY ( column )

  26. 唯一索引：ALTER TABLE table_name ADD UNIQUE ( column )
  27. 普通索引：ALTER TABLE table_name ADD INDEX index_name ( column )
  28. 全文索引：ALTER TABLE table_name ADD FULLTEXT ( column)

  29. 多列索引：ALTER TABLE table_name ADD INDEX index_name ( column1, column2, column3 )

    13.优化器的执行过程

  30. 根据搜索条件，找出可能使用的索引。

  31. 计算全表扫描的代价。
  32. 计算使用不同索引执行查询的代价。
  33. 对比各种执行方案的代价，找出成本最低的一个。