一、实验目的

1、掌握Python开发应用程序的步骤；
2、掌握实验平台（推荐Pycharm）的使用方法及使用步骤；
2、熟悉Python语言的基本要素，包括基本数据类型、数组等；
3、熟悉Python程序控制的几种流程；

二、实验环境

装有Python运行环境、Pycharm平台的PC电脑一台

三、实验内容

1、编写一个程序，将用户输入的两个变量进行相互交换。要求不使用临时变量实现。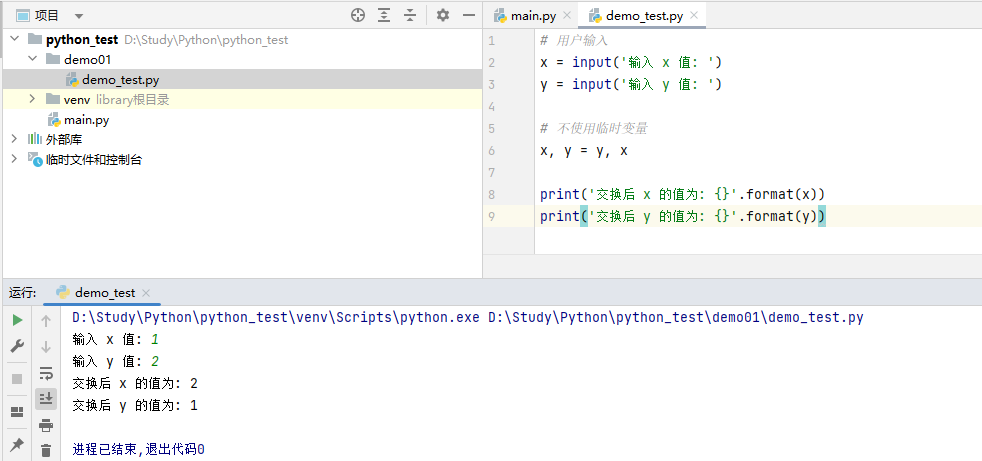

2、有四个数字：1、2、3、4，能组成多少个互不相同且无重复数字的三位数？各是多少？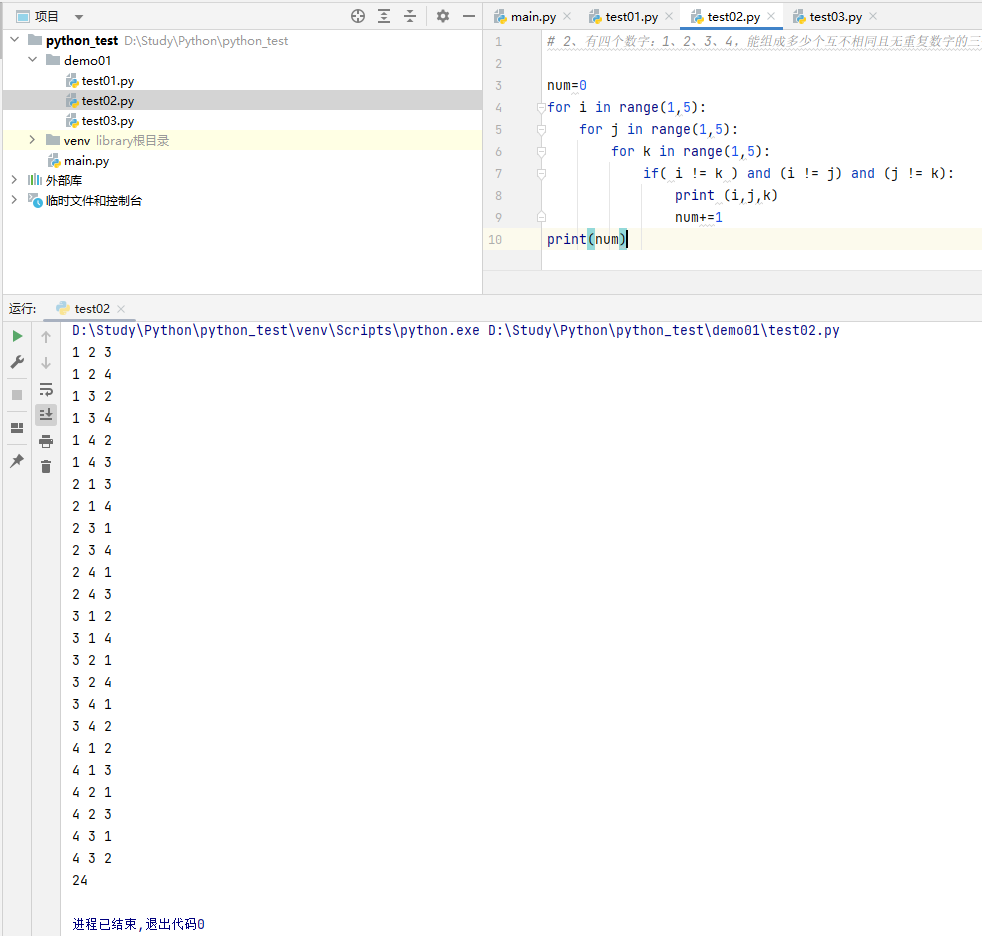

3、输入某年某月某日，判断这一天是这一年的第几天？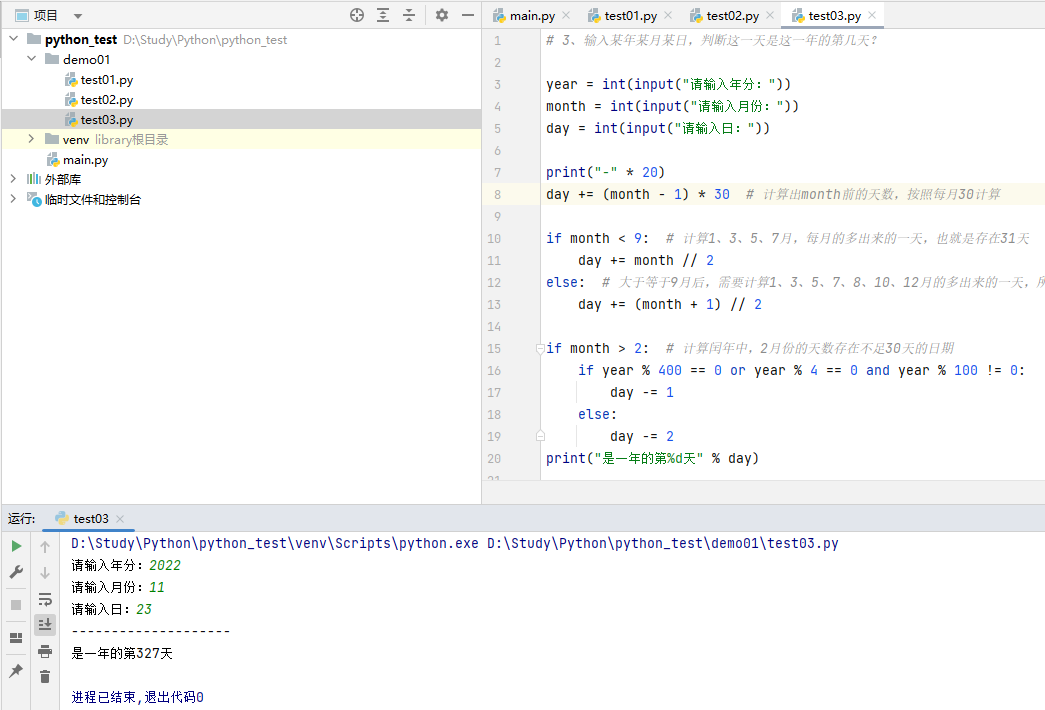

4、所谓“水仙花数”是指一个三位数，其各位数字立方和等于该数本身。例如：153是一个“水仙花数”，因为153=1的三次方＋5的三次方＋3的三次方。利用for循环控制100-999个数，每个数分解出个位，十位，百位。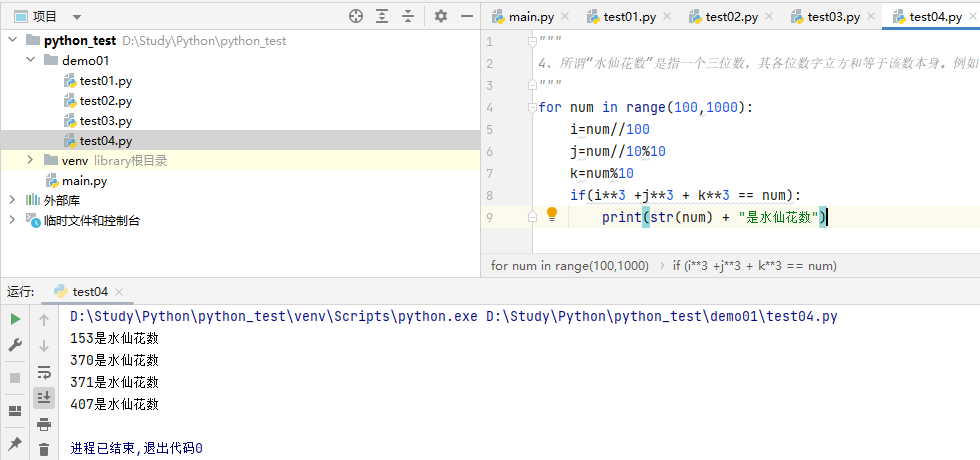

5、如果一个n位正整数等于其各位数字的n次方之和,则称该数为阿姆斯特朗数。 例如1^3 + 5^3 + 3^3 = 153。1000以内的阿姆斯特朗数： 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407。请编写程序，检测用户输入的数字是否为阿姆斯特朗数。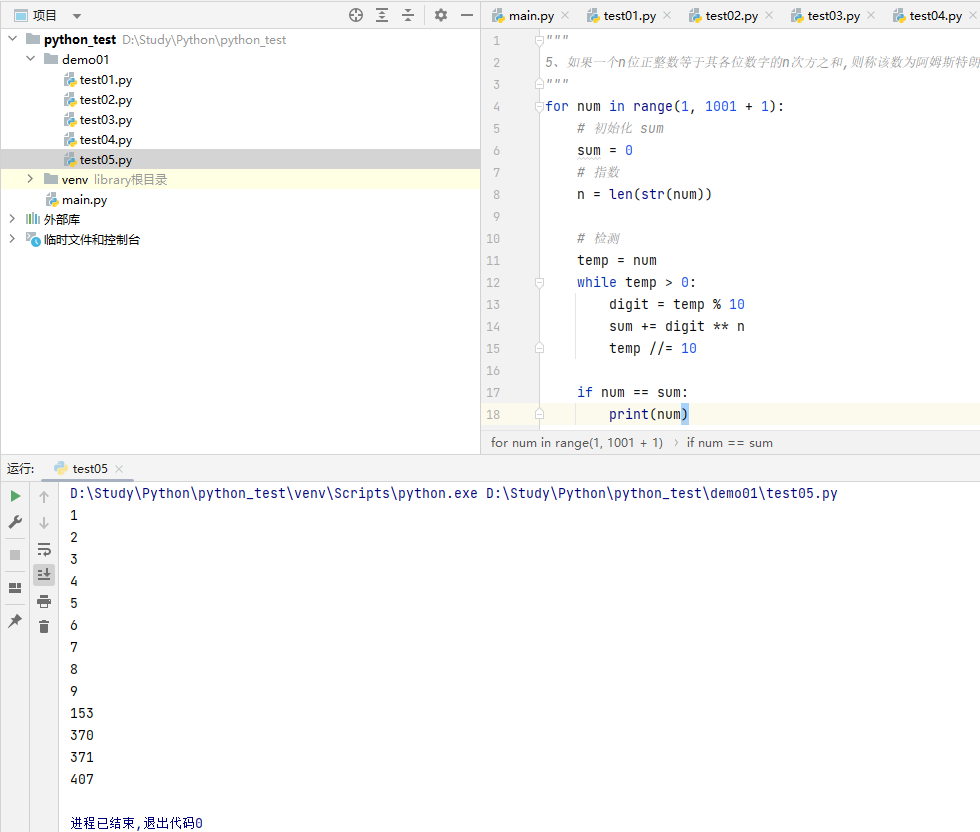

6、素数（prime number）又称质数，有无限个。除了1和它本身以外不再被其他的除数整除。请编写一个程序，输出指定范围内的素数：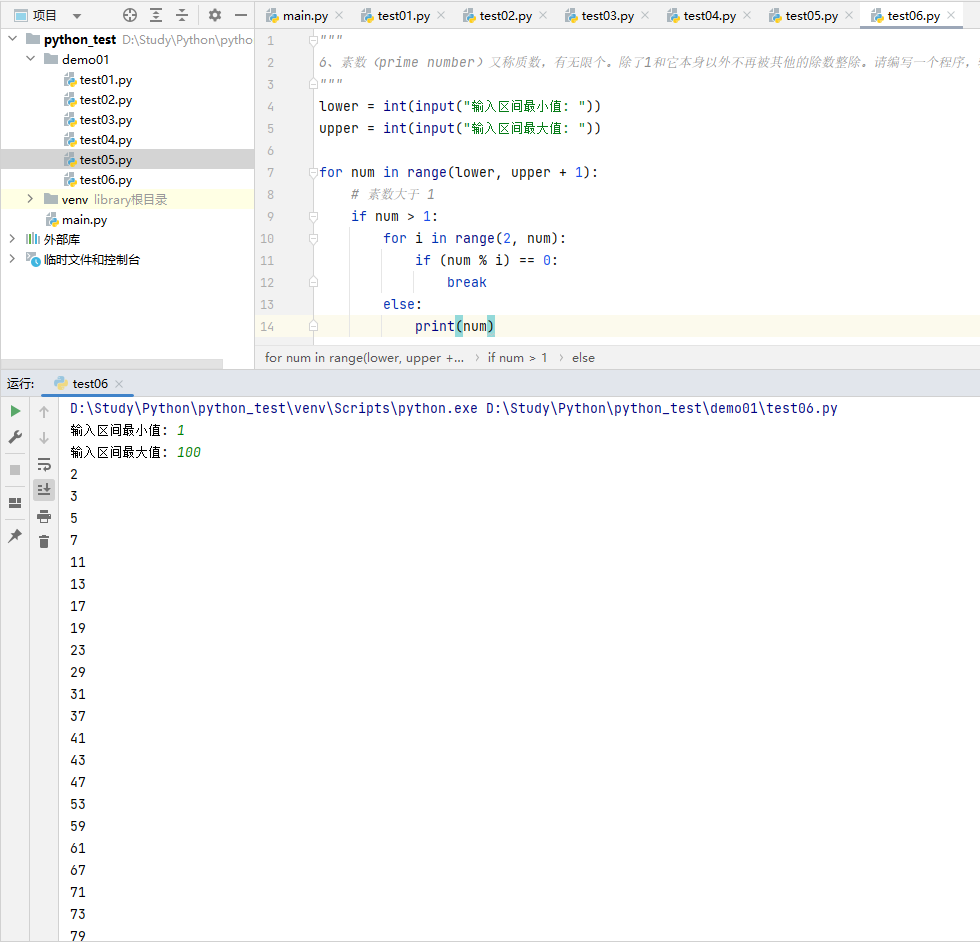

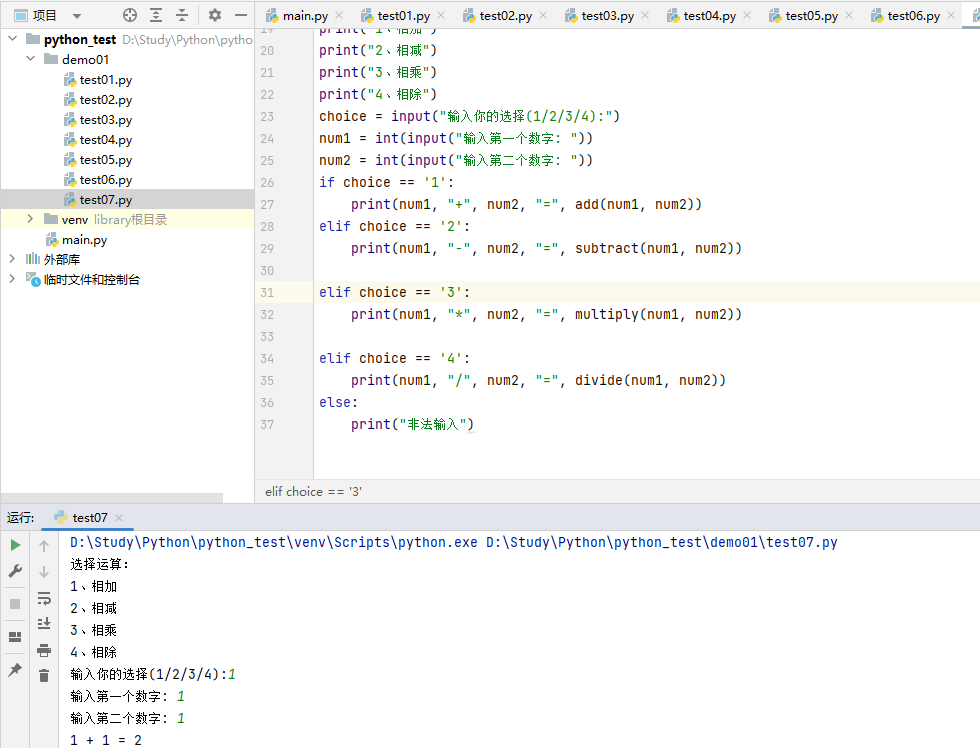
7、编写一个程序，实现简单计算器实现，包括两个数基本的加减乘除运算。

"""
7、编写一个程序，实现简单计算器实现，包括两个数基本的加减乘除运算。
"""
# 定义函数
def add(x, y):
    """相加"""
    return x + y
def subtract(x, y):
    """相减"""
    return x - y
def multiply(x, y):
    """相乘"""
    return x * y
def divide(x, y):
    """相除"""
    return x / y
# 用户输入
print("选择运算：")
print("1、相加")
print("2、相减")
print("3、相乘")
print("4、相除")
choice = input("输入你的选择(1/2/3/4):")
num1 = int(input("输入第一个数字: "))
num2 = int(input("输入第二个数字: "))
if choice == '1':
    print(num1, "+", num2, "=", add(num1, num2))
elif choice == '2':
    print(num1, "-", num2, "=", subtract(num1, num2))
elif choice == '3':
    print(num1, "*", num2, "=", multiply(num1, num2))
elif choice == '4':
    print(num1, "/", num2, "=", divide(num1, num2))
else:
    print("非法输入")

8、编写程序，解一元二次方程 ax^2+bx+c=0。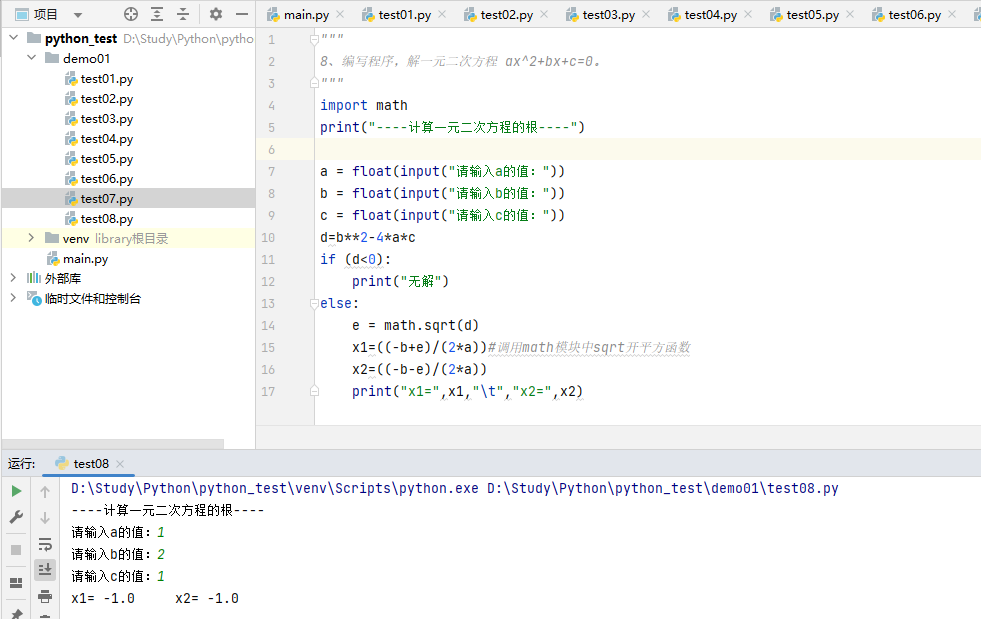

9、某个公司采用公用电话传递数据，数据是四位的整数，在传递过程中是加密的，加密规则如下：每位数字都加上5,然后用和除以10的余数代替该数字，再将第一位和第四位交换，第二位和第三位交换。

10、猜数游戏。
编写程序模拟猜数游戏。程序运行时，系统生成一个随机数，然后提示用户进行猜测，并根据用户输入进行必要的提示（猜对了、太大了、太小了），如果猜对则提前结束程序，如果次数用完仍没有猜对，提示游戏结束并给出正确答案。

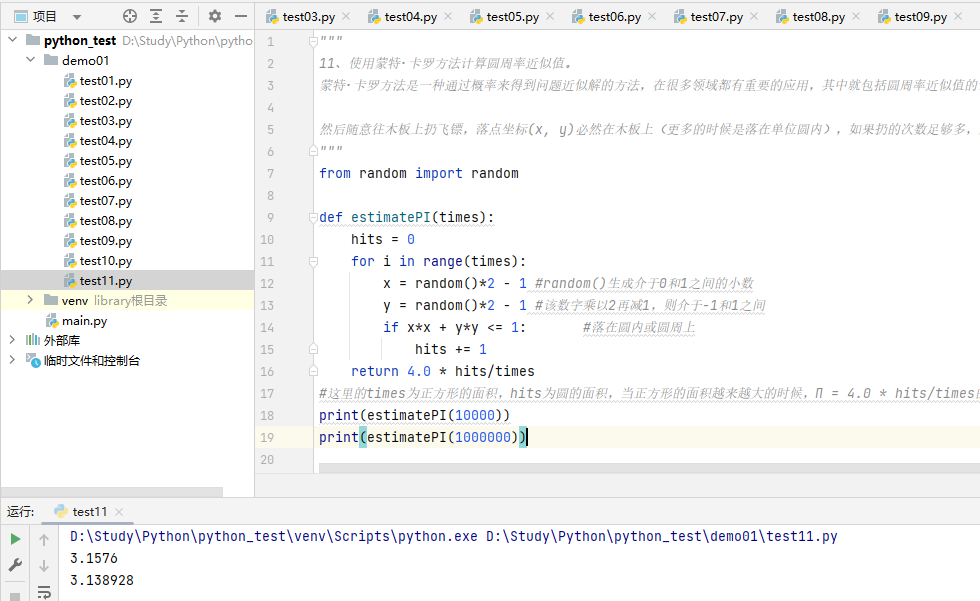
11、使用蒙特·卡罗方法计算圆周率近似值。
蒙特·卡罗方法是一种通过概率来得到问题近似解的方法，在很多领域都有重要的应用，其中就包括圆周率近似值的计算问题。假设有一块边长为 2 的正方形木板，上面画一个单位圆，如下图所示。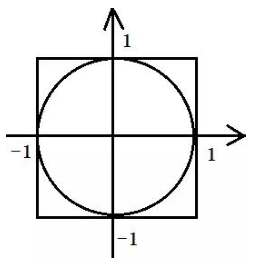

然后随意往木板上扔飞镖，落点坐标(x, y)必然在木板上（更多的时候是落在单位圆内），如果扔的次数足够多，那么落在单位圆内的次数除以总次数再乘以 4，这个数字会无限逼近圆周率的值。这就是蒙特·卡罗发明的用于计算圆周率近似值的方法。编写程序，模拟蒙特·卡罗计算圆周率近似值的方法，输入掷飞镖次数，然后输出圆周率近似值。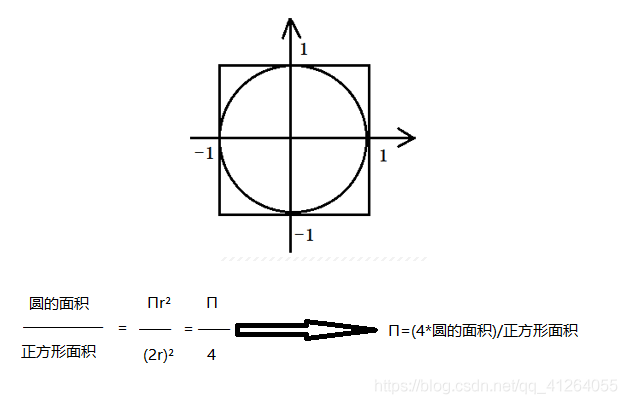

心得体会

练习了python的基本语法
练习了PyCharm 2022.2.3的使用