题目描述:

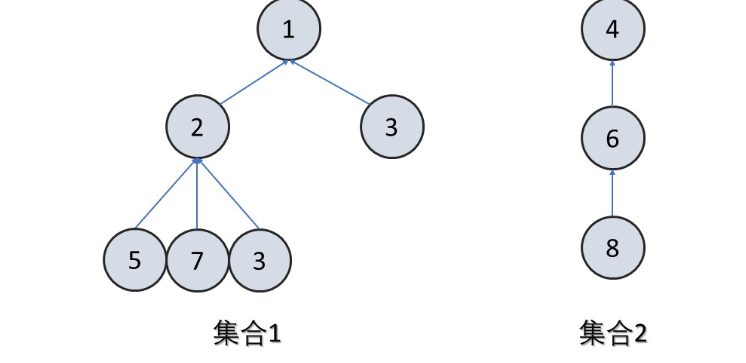
image.png

image.png
image.png

题解：

image.png
可以看到，如果节点是相互连通的（从一个节点可以到达另一个节点），那么他们在同一棵树里，或者说在同一个集合里，或者说他们的祖先是相同的。

（1）初始化
当把一个新节点添加到并查集中，它的父节点应该为空，同时集合数量+1
（2）合并两个节点
如果发现两个节点是连通的，那么就要把他们合并，也就是他们的祖先是相同的。谁做父节点一般是没有区别的。同时集合数量-1
（3）查找祖先和路径压缩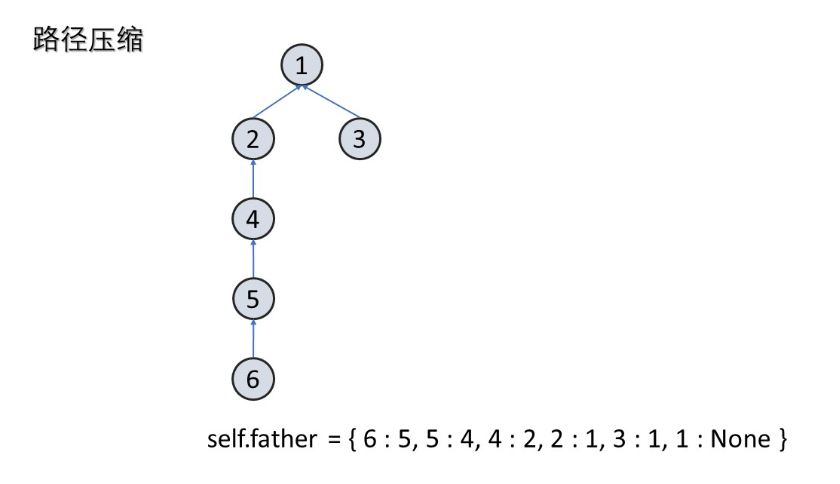
image.png
如果节点的父节点不为空，那就不断迭代
这里有一个优化的点：如果我们树很深，比如说退化成链表，那么每次查询的效率都会非常低。所以我们要做一下路径压缩。也就是把树的深度固定为二。

这么做可行的原因是，并查集只是记录了节点之间的连通关系，而节点相互连通只需要有一个相同的祖先就可以了。

  1. class UnionFind:
  2.     def __init__(self):
  3.         # 记录父结点
  4.         self.father = {}
  5.         # 记录集合的数量
  6.         self.num_of_sets = 0
  8.     def find(self,x):
  9.         root = x
  10.         #寻找父结点
  11.         while self.father[root] != None:
  12.             root = self.father[root]
  13.         #路径压缩
  14.         while x != root:
  15.             original_father = self.father[x]
  16.             self.father[x] = root
  17.             x = original_father
  19.         return root
  21.     #聚合两个结点
  22.     def merge(self,x,y):
  23.         root_x,root_y = self.find(x),self.find(y)
  24.         #如果父结点不同，则合并
  25.         if root_x != root_y:
  26.             self.father[root_x] = root_y
  27.             # 集合的数量-1
  28.             self.num_of_sets -= 1
  30.     def add(self,x):
  31.         if x not in self.father:
  32.             self.father[x] = None
  33.             # 集合的数量+1
  34.             self.num_of_sets += 1
  36. class Solution:
  37.     def findCircleNum(self, M: List[List[int]]) -> int:
  38.         uf = UnionFind()
  39.         for i in range(len(M)):
  40.             uf.add(i)
  41.             for j in range(i):
  42.                 if M[i][j]:
  43.                     uf.merge(i,j)
  45.         return uf.num_of_sets