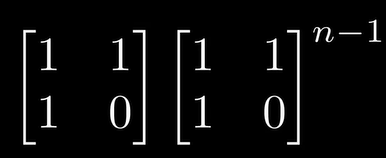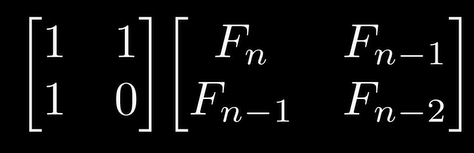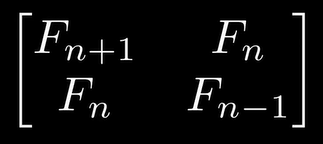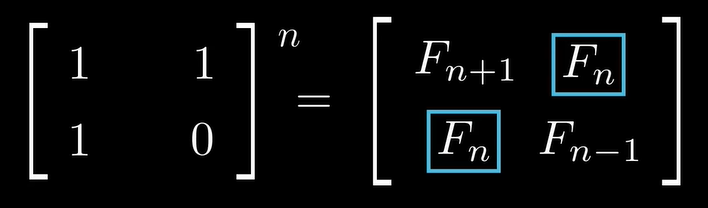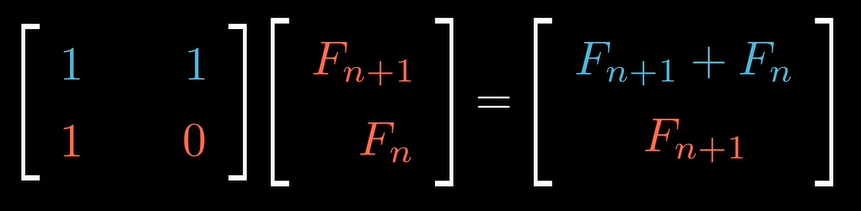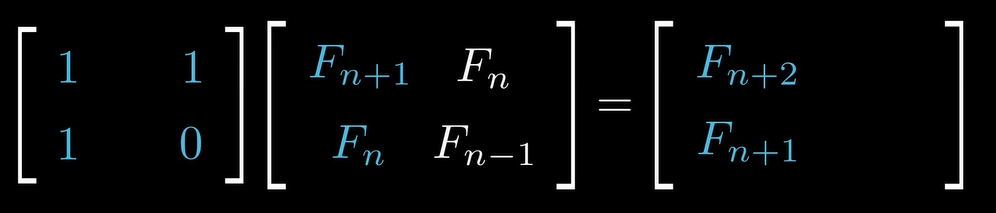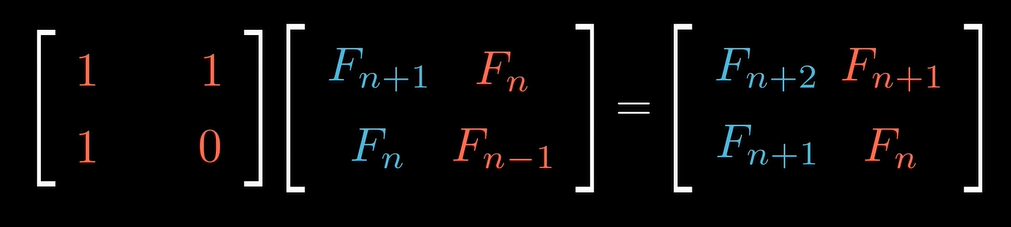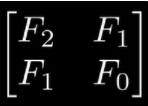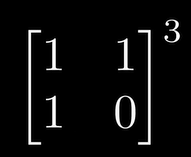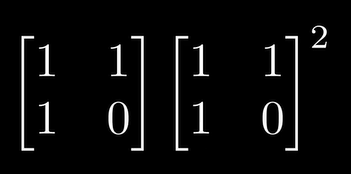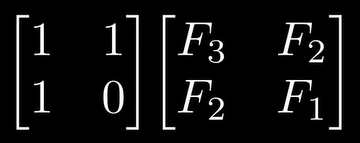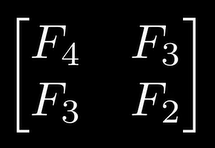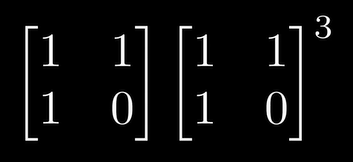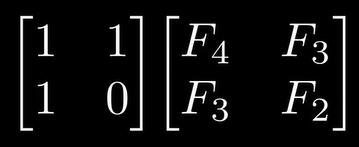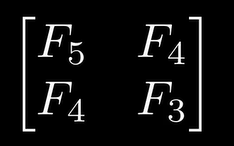题目

实验I：体验神奇的算法
本实验要求根据给定的正整数n计算第n个斐波那契数。课堂上已经讲过4种不同的算法，请选择自己最熟悉的编程语言实现这些算法来体验算法求解问题的神奇，下列基本要求必须完成：
1、 设计一个交互界面（例如菜单）供用户选择，如果可能，最好是一个图形化用户界面。
image.png
2、 利用迭代算法寻找不超过编程环境能够支持的最大整数的斐波那契数是第几个斐波那契数。（Java： 231-1 for int, 263-1 for long）

  1. java int最大值是：2147483647
  3. int 类型数占４个byte.
  5. 1byte=8bit
  7. 也就是有32个bit占位符
  1.  //找到超过int最大值之前的一个斐波拉契数字是第几个
  2.     public static int findMax(){
  3.         int index = 2;
  4.         int first = 1,second = 1;
  5.         int cur = 0;
  6.         while(first + second > 0){
  7.             cur = first + second;
  8.             first = second;
  9.             second = cur;
  10.             index++;
  11.         }
  12.         System.out.println("没超过int的最大斐波那契数字为:"+cur+"位于"+index);
  13.         return index;
  14.     }

image.png
3、 根据第二步计算的最大的斐波那契数序号n，采用递归方式计算第n个斐波那契数，看其是否可以在1分钟内完成。

  1. case 2:
  2.     if(maxIndex == -1){
  3.         System.out.println("请至少先运行第一个功能再来试试吧");
  4.         break;
  5.     }
  6.     //long start = new Date().getTime();
  7.     long start = System.currentTimeMillis();
  8.     recur(maxIndex);
  9.     long end = System.currentTimeMillis();
  10.     System.out.println("用了" + (end - start) / 1000 + "秒");
  11.     break;
  1.     //递归求解需要多少秒呢？
  2.     public static int recur(int index){
  3.         if(index == 1 || index == 2){
  4.             return 1;
  5.         }
  6.         return recur(index - 1) + recur(index - 2);
  7.     }

image.png
4、 利用递归算法计算你的计算机能够在30秒内计算出的最大斐波那契数是第几个，计算出下一个斐波那契数的时间是多少，利用迭代算法求解同样的问题。

  1. case 3:
  2.     int timeIndex = timeSearchForRecur();
  3.     long s = System.currentTimeMillis();
  4.     recur(timeIndex + 1);
  5.     long e = System.currentTimeMillis();
  6.     System.out.println("第" + (timeIndex + 1)+ "位斐波那契数递归用了" + (e - s) / 1000 + "秒 (超过了30s3)");
  7.     break;
  1. //找到30s内可以递归出来的最大斐波那契数列（递归）
  2. public static int timeSearchForRecur(){
  3.     int index = 1;
  4.     while(true){
  5.         long cur = System.currentTimeMillis();
  6.         recur(index);
  7.         long end = System.currentTimeMillis();
  8.         if(end - cur >= 30 * 1000){
  9.             System.out.println("(递归)30s内最大的斐波那契数位于" + (index - 1));
  10.             return index - 1;
  11.         }
  12.         index++;
  13.     }
  14. }

image.png
5、 利用公式F(n) = [fn/sqrt(5)]快速计算第n个斐波那契数，找出出现误差时的最小n值。
image.png

  1. //公式求解快速计算出第n个斐波那契数字
  2. public static void mathForFib(int index){
  3.     long result = 1;
  4.     float temp = (float) Math.sqrt(5.0);
  6.     result = (long)((Math.pow((1 + temp) / 2, index) - Math.pow((1 - temp) / 2, index)) / temp);
  8.     System.out.println("第" + index + "位的" + result);
  9. }

image.png

  1. //公式求解快速计算出第n个斐波那契数字，找出出现误差最小的n值
  2. public static void mathFib(){
  3.     int index = 1;
  4.     long result = 1;
  5.     float temp = (float) Math.sqrt(5.0);
  6.     while(true){
  7.         result = (long)((Math.pow((1 + temp) / 2, index) - Math.pow((1 - temp) / 2, index)) / temp);
  8.         if(result != fib(index)){
  9.             break;
  10.         }
  11.         index++;
  12.     }
  14.     System.out.println("出现误差的最小n值为第" + index + "位的" + result);
  15. }

image.png
6、 利用矩阵相乘方法计算第n个斐波那契数。
image.png
复杂度分析
时间复杂度：O(\log n)O(logn)。
空间复杂度：O(1)O(1)。
image.png

参考代码：http://blog.sina.com.cn/s/blog_6ea2c6a20100x359.html

  1.  static long matrix[][] = {{1,1},{1,0}};
  2.     //    矩阵方式求斐波拉契数列
  3.     public static long matrixForFib(int index){
  4.         if (index <= 0) {
  5.             throw new RuntimeException("输入参数小于1");
  6.         }
  7.         if (index == 1 || index == 2) {
  8.             return 1;
  9.         }
  10.         long[][] tem = matrix;
  11.         for (int i = 1; i < index - 2; i++) {
  12.             //已知一开始tmp和matrix然后迭代计算到最后
  13.             tem = doMatrix(tem,matrix);
  14.         }
  15.         return tem[0][0] + tem[1][0];
  16.     }
  18.     public static long[][] doMatrix(long[][] a,long[][] b){
  19.         long[][] res = new long[2][2];
  20.         res[0][0] = a[0][0] * b[0][0] + a[0][1] * b[1][0];
  21.         res[0][1] = a[0][0] * b[0][1] + a[0][1] * b[1][1];
  22.         res[1][0] = a[1][0] * b[0][0] + a[1][1] * b[1][0];
  23.         res[1][1] = a[1][0] * b[0][1] + a[1][1] * b[1][1];
  24.         return res;
  25.     }

image.png
7、 对于相同的输入n值，比较上述四种方法的基本操作次数，以掌握对数、线性和指数增长率的极大差别。

实现代码

  1. package week1;
  3. import java.util.Scanner;
  5. /**
  6.  * @author newThread
  7.  * @className Solution
  8.  * @date 2021/10/15 16:10
  9.  */
  10. class Solution {
  12.     static int max = Integer.MAX_VALUE;
  14.     //找到超过int最大值之前的一个斐波拉契数字是第几个
  15.     public static int findMax(){
  16.         int index = 2;
  17.         int first = 1,second = 1;
  18.         int cur = 0;
  19.         while( first + second > 0){
  20.             cur = first + second;
  21.             first = second;
  22.             second = cur;
  23.             index++;
  24.         }
  25.         System.out.println("没超过int的最大斐波那契数字为:"+cur+"位于"+index);
  26.         return index;
  27.     }
  29.     public static long fib(int index){
  30.         if(index == 1 || index == 2){
  31.             return 1;
  32.         }
  33.         long first = 1,second = 1;
  34.         long cur = 0;
  35.         index = index - 2;
  36.         while(index > 0){
  37.             cur = first + second;
  38.             first = second;
  39.             second = cur;
  40.             index--;
  41.         }
  42.         return cur;
  43.     }
  45.     //递归求解需要多少秒呢？
  46.     public static int recur(int index){
  47.         if(index == 1 || index == 2){
  48.             return 1;
  49.         }
  50.         return recur(index - 1) + recur(index - 2);
  51.     }
  53.     //找到30s内可以递归出来的最大斐波那契数列（递归）
  54.     public static int timeSearchForRecur(){
  55.         int index = 1;
  56.         while(true){
  57.             long cur = System.currentTimeMillis();
  58.             recur(index);
  59.             long end = System.currentTimeMillis();
  60.             if(end - cur >= 30 * 1000){
  61.                 System.out.println("(递归)30s内最大的斐波那契数位于" + (index - 1));
  62.                 return index - 1;
  63.             }
  64.             index++;
  65.         }
  66.     }
  69.     //找到30s内可以递归出来的最大斐波那契数列（递归）
  70.     public static int timeSearchForDieDai(){
  71.         int index = 1;
  72.         while(true){
  73.             long cur = System.currentTimeMillis();
  74.             fib(index);
  75.             long end = System.currentTimeMillis();
  76.             if(end - cur >= 30 * 1000){
  77.                 System.out.println(end -cur);
  78.                 System.out.println("(迭代)30s内最大的斐波那契数位于" + (index - 1));
  79.                 return index - 1;
  80.             }
  81.             index++;
  82.         }
  83.     }
  85.     //公式求解快速计算出第n个斐波那契数字，找出出现误差最小的n值
  86.     public static void mathFib(){
  87.         int index = 1;
  88.         long result = 1;
  89.         float temp = (float) Math.sqrt(5.0);
  90.         while(true){
  91.             result = (long)((Math.pow((1 + temp) / 2, index) - Math.pow((1 - temp) / 2, index)) / temp);
  92.             if(result != fib(index)){
  93.                 break;
  94.             }
  95.             index++;
  96.         }
  98.         System.out.println("出现误差的最小n值为第" + index + "位的" + result);
  99.     }
  101.     //公式求解快速计算出第n个斐波那契数字
  102.     public static void mathForFib(int index){
  103.         long result = 1;
  104.         float temp = (float) Math.sqrt(5.0);
  106.         result = (long)((Math.pow((1 + temp) / 2, index) - Math.pow((1 - temp) / 2, index)) / temp);
  108.         System.out.println("第" + index + "位的" + result);
  109.     }
  112.     static long matrix[][] = {{1,1},{1,0}};
  113.     //    矩阵方式求斐波拉契数列
  114.     public static long matrixForFib(int index){
  115.         if (index <= 0) {
  116.             throw new RuntimeException("输入参数小于1");
  117.         }
  118.         if (index == 1 || index == 2) {
  119.             return 1;
  120.         }
  121.         long[][] tem = matrix;
  122.         for (int i = 1; i < index - 2; i++) {
  123.             //已知一开始tmp和matrix然后迭代计算到最后
  124.             tem = doMatrix(tem,matrix);
  125.         }
  126.         return tem[0][0] + tem[1][0];
  127.     }
  129.     public static long[][] doMatrix(long[][] a,long[][] b){
  130.         long[][] res = new long[2][2];
  131.         res[0][0] = a[0][0] * b[0][0] + a[0][1] * b[1][0];
  132.         res[0][1] = a[0][0] * b[0][1] + a[0][1] * b[1][1];
  133.         res[1][0] = a[1][0] * b[0][0] + a[1][1] * b[1][0];
  134.         res[1][1] = a[1][0] * b[0][1] + a[1][1] * b[1][1];
  135.         return res;
  136.     }
  138.     public static void main(String[] args) {
  139.         Scanner scanner = new Scanner(System.in);
  140.         int maxIndex = -1;
  141.         while(true){
  142.             System.out.println("-------------------------实验I：体验神奇的算法----------------------------|\n");
  143.             System.out.println("|     1.利用迭代算法找出不超过编程环境能够支持的最大整数的斐波那契数是第几个数。     |                             ");
  144.             System.out.println("|     2.根据选项1的序号n，用递归计算第n个斐波那契数．看其是否可以在1分钟内完成。    |                             ");
  145.             System.out.println("|     3.利用递归算法计算你的计算机能够在30秒内计算出的最大斐波那契数是第几个，      |\n" +
  146.                                "|       并且计算出下一个斐波那契数的时间                                     |");
  147.             System.out.println("|     4.利用公式计算第n个斐波那契数                                        |                                 ");
  148.             System.out.println("|     5.利用公式计算出现误差的最小斐波那契是第几个                            |                                ");
  149.             System.out.println("|     6.利用矩阵计算第n个斐波那契数                                        |                                ");
  150.             System.out.println("|     7.退出系统                                                       |                                 ");
  151.             System.out.println("|----------------------------------------------------------------------");
  152.             System.out.println("请输入对应选项序号：");
  153.             int choice = scanner.nextInt();
  154.             switch (choice){
  155.                 case 1:
  156.                     maxIndex = findMax();
  157.                     break;
  158.                 case 2:
  159.                     if(maxIndex == -1){
  160.                         System.out.println("请至少先运行第一个功能再来试试吧");
  161.                         break;
  162.                     }
  163.                     //long start = new Date().getTime();
  164.                     long start = System.currentTimeMillis();
  165.                     recur(maxIndex);
  166.                     long end = System.currentTimeMillis();
  167.                     System.out.println("用了" + (end - start) / 1000 + "秒");
  168.                     break;
  169.                 case 3:
  170.                     int timeIndex = timeSearchForRecur();
  171.                     long s = System.currentTimeMillis();
  172.                     recur(timeIndex + 1);
  173.                     long e = System.currentTimeMillis();
  174.                     System.out.println("第" + (timeIndex + 1)+ "位斐波那契数递归用了" + (e - s) / 1000 + "秒 (超过了30s3)");
  175.                     break;
  176.                 case 4:
  177.                     System.out.println("您想求出第几位斐波那契数？");
  178.                     int index = scanner.nextInt();
  179.                     mathForFib(index);
  180.                     break;
  181.                 case 5:
  182.                     mathFib();
  183.                     break;
  184.                 case 6:
  185.                     System.out.println("您想求出第几位斐波那契数？");
  186.                     int matrixIndex = scanner.nextInt();
  187.                     long l = matrixForFib(matrixIndex);
  188.                     System.out.println("第"+ matrixIndex + "位的斐波那契数为" + l);
  189.                     break;
  190.                 case 7:
  191.                     return;
  192.                 default:
  193.                     System.out.println("请输入正确的选项");
  194.                     break;
  195.             }
  196.         }
  197.     }
  198. }

1.矩阵求解斐波那契数列

1次平方阶

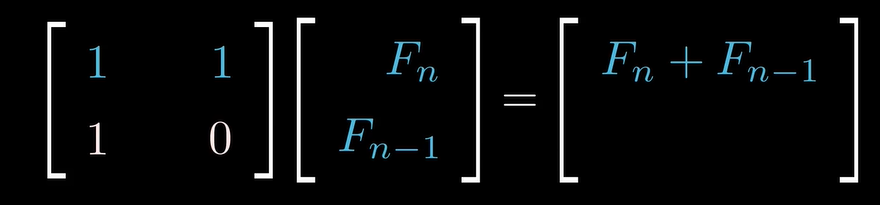
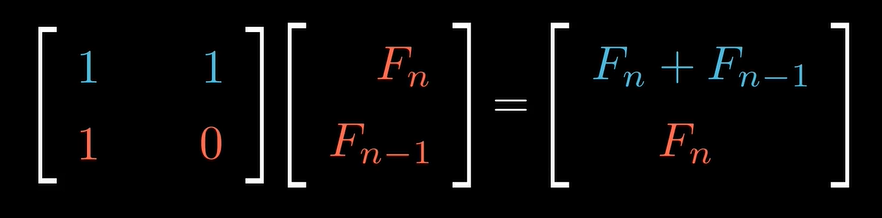
image.png
1
image.png
image.png
2.斐波那契数列原则
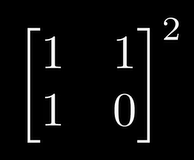
image.png
3.继续推演

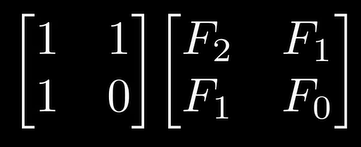
image.png
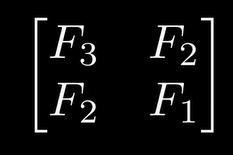
image.png
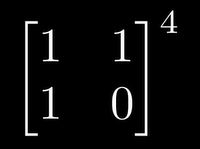
image.png
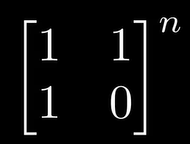
image.png
结论：
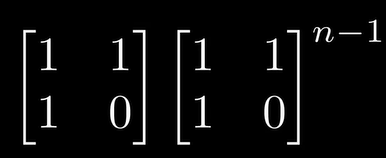
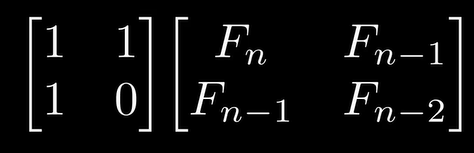
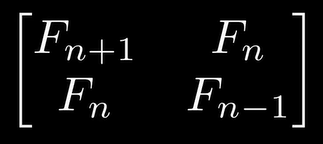
image.png

2次平方阶

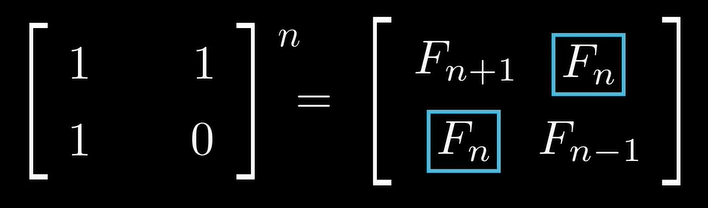
image.png
1.
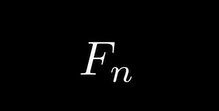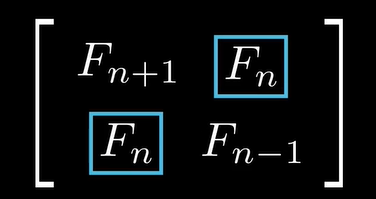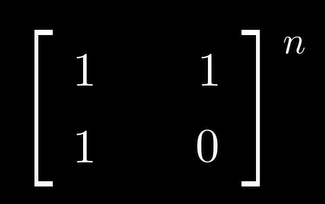
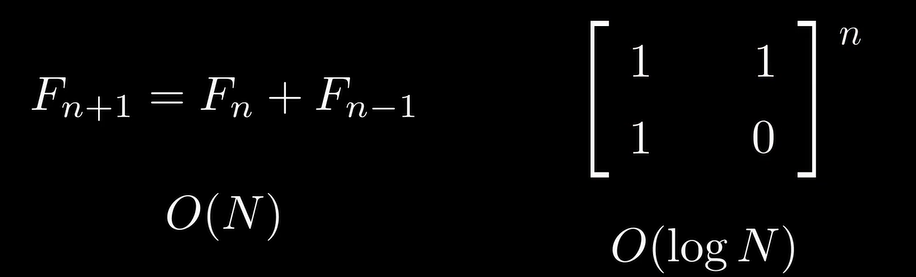
image.png
2.
image.png
结论：
image.png

3次平方阶

image.png
1.
image.png
image.png
结论：
image.png

4次平方阶

image.png

1.
image.png
image.png
结论：
image.png
image.png

n次平方阶

image.png
1.
image.png
image.png
image.png
结论：
image.png
最终结论：

image.png =image.png=image.png
image.png
C语言代码：

  1. //通过矩阵相乘来计算
  2. long matx(int n)//利用矩阵相乘方法计算第n个斐波那契数   n-->索引值+1
  3. {
  4.     //x=f0,y=f1,t=f2-->x=fn-1,y=fn,t=fn-1(推演下一次x的位置),p-->斐波那契数列的第几个,n是最终值，p是推演具体值（对应左上角fn+1）
  5.     int x = 0, y = 1, t = 1, p = 2;
  6.     //i是起始值：i=1,从第一个斐波那契数列开始
  7.     int i;
  8.     //temp1暂存fn-1的值
  9.     //temp2暂存fn+1的值
  10.     int temp1 = 0;
  11.     int temp2 = 0;
  12.     for (i = 1; i < n; i++) {
  13.         //1.求矩阵右下角
  14.         //fn-1的值赋值给temp1
  15.         temp1 = x;
  16.         //fn-2*0+fn-1*1=fn-1
  17.         x = x * 0 + y * 1;
  18.         //2.求矩阵左下角、右上角
  19.         //1*fn-1+1*fn-2=fn
  20.         y = temp1 * 1 + y * 1;
  21.         //求矩阵左上角
  22.         //fn+1的值暂存给temp2
  23.         temp2 = t;
  24.         //fn-1*0+fn=fn+1
  25.         t = t * 0 + p * 1;
  26.         //fn-1*1+fn*1=fn+1
  27.         p = temp2 * 1 + p * 1;
  28.     }
  29.     return y;
  30. }

此题结构如下:
1、实验I：体验神奇的算法 - 图42
image.pngimage.pngimage.pngimage.png