LeetCode.84 柱状图中最大的矩形

原题链接

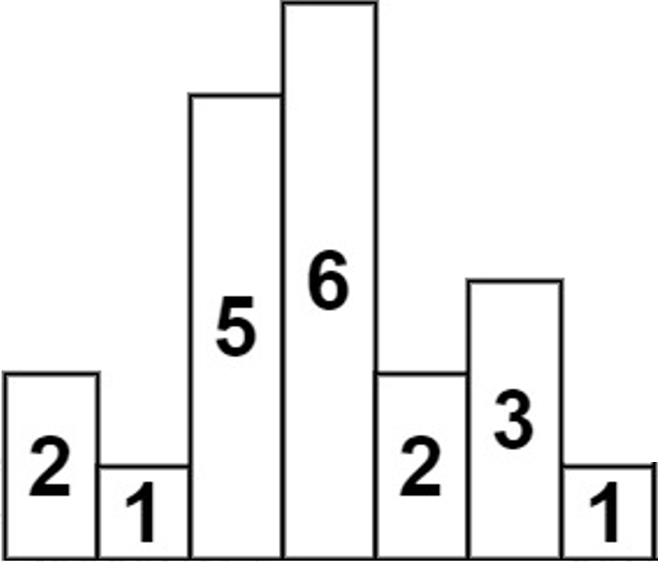
其实对于每根柱子，都有一个独属于它的矩形。
矩形的宽也就是柱子本身的高度，长度则由从这根柱子开始往右第一根比它矮的柱子的位置r[i]和从这根柱子开始往左第一根比它矮的柱子的位置l[i]决定。
所以题目变成了：对于每根柱子i，确定从这根柱子开始往右第一根比它矮的柱子的位置r[i]和从这根柱子开始往左第一根比它矮的柱子的位置l[i]，典型的单调栈的题目。
数组r每个元素要初始为n，数组l每个元素要初始为-1，这是因为对于某根柱子，它左边或者右边没有比他矮的柱子，那么此时属于这根柱子独有的矩形的长可以一直延申至左边界或者右边界。
最后，对于每根柱子确定的矩形，找到面积最大的那个即可。

AC代码如下：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> s;
        int n = heights.size(), ans = -1;
        int r[n], l[n];
        fill(l, l + n, -1);
        fill(r, r + n, n);
        for (int i = 0; i < n; i++)
        {
            while (s.size() > 0 && heights[i] < heights[s.top()])
                r[s.top()] = i, s.pop();
            s.push(i);
        }
        s = stack<int>();
        for (int i = n - 1; i >= 0; i--)
        {
            while (s.size() > 0 && heights[i] < heights[s.top()])
            l[s.top()] = i, s.pop();
            s.push(i);
        }
        for (int i = 0; i < n; i++)
            ans = max(ans, (r[i] - l[i] - 1) * heights[i]);
        return ans;
    }
};